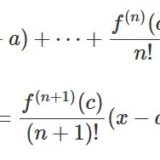どうも、木村(@kimu3_slime)です。
解析学において、逐次近似法、不動点定理は重要なテーマのひとつです。今回はそれをわかりやすく説明します。
例:ニュートン法
まずは例として有名なニュートン法(Newton’s method)を簡単に紹介しましょう。
画像引用:Animation of Newton’s method. Ralf Pfeifer – Wikipedia
ニュートンの逐次近似法
区間\(I=[a,b]\)で常に\(f”(x)>0\)であり、かつ\(f(a)f(b)<0\)とする。いま\(f(x_0)>0\)となる\(x_0\in (a,b)\)を一つとり、帰納的に
\[ \begin{aligned}x_{n+1}=x_n -\frac{f(x_n)}{f'(x_n)}\end{aligned} \]
と定義する。このとき数列\(\{x_n\}_{n\in \mathbf{N}}\)は単調に、\(I\)における\(f\)の唯一つの零点\(c\)に収束する。
引用:杉浦 解析入門 Ⅰ p.105
例えば、\(f(x)=x^2-2\)とすれば、\(\sqrt 2\)の値を段階的に計算することができます。電卓や計算機を使わず、手計算でもルートの値が求められますね。
逐次近似法と呼ばれるのは、数列が\(x_0,x_1,x_2,\dots\)と進むごとに、少しずつ真の解に近づいていくからです。
ニュートン法は、プログラムによる数値計算の簡単な例として、よく扱われるテーマとなっています。
縮小写像の不動点定理
少し話を変えます。
縮尺が異なる地図を2つ用意し、一方をもう一方に重ねているようすをイメージします。このとき、必ずどこかに一点重なっている場所が存在することがわかりますか? これは、どんな地図でも、どんな縮尺の縮め方でも起こります。
地図を床に置いてみれば、地図上の地点と現実の地点が重なる場所が必ずあります。(もちろん、地球を局所的に平面と見て…の話ですが)
これは地図の性質によるものではなく、解析学によって証明される不動点定理と呼ばれるものです。
縮小写像、不動点とは
\(f:\mathbb{R}^N\to\mathbb{R}^N\)を写像(関数)とします。
定数\(0<K<1\)で、任意の\(x,y\in \mathbb{R}^N\)に対し、
\[ \begin{aligned}\|f(x)-f(y)\|\leq K\|x-y\|\end{aligned} \]
なるものが存在するとき、\(f\)を縮小写像(contraction mapping)と呼びます。
異なる2点\(x,y\)を写像\(f\)によって飛ばすと、元の距離\(\|x-y\|\)より飛ばした先の距離\(\|f(x)-f(y)\|\)の方が必ず小さくなることを意味していますね。
不動点(fixed point)とは、\(f(x)=x\)となる点のこと。文字通り動かない点です。
不動点定理
縮小写像には、必ず不動点が存在するという性質があります。
縮小写像の不動点定理
\(f:\mathbb{R}^N\to\mathbb{R}^N\)を縮小写像、\(x_0 \in \mathbb{R}^N\)とします。そして、点列\(\{x_n\}_{n\in \mathbb{N}}\)を
\[ \begin{aligned}x_{n+1}=f(x_n)\end{aligned} \]
によって定めると、点列\(\{x_n\}_{n\in \mathbb{N}}\)は\(\mathbb{R}^N\)内で収束します。
\[ \begin{aligned}x^*=\lim_{n\to \infty}x_n\end{aligned} \]
とすると、\(x^*\)は\(f\)の不動点です。また、唯一の不動点でもあります。
証明は詳しくは行いません。
点列\(\{x_n\}_{n\in \mathbb{N}}\)がコーシー列であることを示せば、\(\mathbb{R}^N\)が完備であることから収束します。
その極限が唯一の不動点であることを確かめれば良いだけです。
縮小写像の性質を用いれば、\(\|x_m-x_n\|\)が\(K\)の\(m,n\)を含むべき乗で抑えられて、限りなく小さくできます。
参考:梶原 大学院への解析学演習 p.104
この不動点定理は、どのような\(x_0 \in \mathbb{R}^N\)からスタートしても、繰り返し\(f\)を作用させることで、不動点\(x^*\)に収束します。
このような方法は、逐次近似法、反復法(iteration)と呼ばれています。
不動点定理の応用
不動点定理は、解析学のさまざまな場面で活躍します。
ピカールの逐次近似法
常微分方程式の初期値問題を不動点定理を使って解く方法は、ピカールの逐次近似法と呼ばれています。
\[ \begin{aligned}y’=f(x,y),y(\alpha)=\beta\end{aligned} \]
を解くために、これを積分方程式に書き換えてから、
\[ \begin{aligned}y_{n+1}(x)=\beta + \int^x _a f(t,y_n(t))dt\end{aligned} \]
と定めて、逐次近似法を用います。これにより、(時間局所的な)解の存在と一意性が示せます。
参考:柳田 常微分方程式論 p.181、黒田 関数解析 pp.208-209
バナッハの不動点定理
縮小写像の不動点定理の定義域は\(\mathbf{R}^N\)でしたが、これはより一般の空間、(バナッハ空間を含む)完備距離空間でも成立します。
バナッハの不動点定理
\(X\)を完備距離空間、\(f:X\to X\)を縮小写像、\(x_0 \in X\)とします。そして、点列\(\{x_n\}_{n\in \mathbb{N}}\)を
\[ \begin{aligned}x_{n+1}=f(x_n)\end{aligned} \]
によって定めると、点列\(\{x_n\}_{n\in \mathbb{N}}\)は\(X\)内で収束します。
\[ \begin{aligned}x^*=\lim_{n\to \infty}x_n\end{aligned} \]
とすると、\(x^*\)は\(f\)の不動点です。また、唯一の不動点でもあります。
このようなセッティングのときは、縮小写像というよりは、むしろ縮小作用素と呼ばれます。
微分方程式を解くために、それを積分形に置き換え、それにより定まる積分作用素が縮小作用素であることを示すことで、解の存在と一意性が示せます。
逐次近似法や不動点定理の話の雰囲気を感じ取っていただけたでしょうか。
不動点定理は、僕の好きな数学の定理のひとつです。
地図の例を挙げれば、直感的に説明しやすいです。いかにも正しそう。でも、なんで正しいと言えるのかに、数学が関わってくる。
そして、方程式の解の存在と一意性を示すという基本的な問題に役立ちつつ、単なる理論的な存在だけでなく、逐次的にそれを求める手続きも用意してくれているのです。
証明も比較的シンプルで覚えることが少なく、2点の距離を不等式を使って評価していくようすは、解析学らしくて面白いと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
ブラウワーの不動点定理
追記:
今回紹介しなかった有名な不動点定理として、ブラウワーの不動点定理、シャウダーの不動点定理があります。(他にもさまざまな不動点定理が存在します)
その主張は、「コンパクトな凸集合からそれ自身への連続写像は、不動点を持つ」というもの。
定義域が限定される代わりに、縮小写像よりゆるい条件、ただ連続であるだけで不動点が保証されます。
イメージとしては、カップに入れたコーヒーをかき混ぜた表面には必ずどこかに渦が存在する、といったもの。地球上の表面には必ず風の吹かない点が存在する。
証明は、位相幾何学的な手法によります。
参考:ブラウワーの不動点定理 – Wikipedia、トポロジー入門 – 春の談話会2016
朝倉書店
売り上げランキング: 303,362