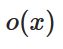どうも、木村(@kimu3_slime)です。
今回は、線形常微分方程式の一般解を簡単に表すのに役立つ、行列の指数関数\(e^A\)という線形代数のアイデアを紹介します。
線形常微分方程式を解こう
1次元の非常に単純な常微分方程式
\[ \begin{aligned}\frac{du}{dt}(t) = a u(t)\end{aligned} \]
の解は、\(u(t)= u(0) e^{at}\)と指数関数を使って表されます。
もしこれが連立線形常微分方程式だったらどうでしょうか。\(u=(u_1,\dots,u_N)\)と\(N\)次元のベクトルであったとして、
\[ \begin{aligned}\frac{du}{dt}(t) = A u(t)\end{aligned} \]
の解はどうなるでしょうか。これが\(u(t)= u(0) e^{At}\)というような式で表されたら嬉しいですね。(正確には、\(u(t)= e^{tA} u(0)\)となる)
実際、そう表されるように、行列の指数関数というものを定義できます。
行列の指数関数とは
そもそも、普通の指数関数、実変数の指数関数\(e^t: \mathbb{R}\to \mathbb{R}\)とは、実数\(t\in \mathbb{R}\)に対して、
\[ \begin{aligned}e^t = 1+ t + \frac{1}{2}t^2 +\cdots = \sum_{k=0}^{\infty} \frac{1}{k!} t^k\end{aligned} \]
と表されるのでした。(テイラー展開。これが指数関数の定義として採用されることも)
ここから類推して、行列を変数とする指数関数\(e^A: M_N \to M_N\)を、
\[ \begin{aligned}e^A = E+ A + \frac{1}{2}A^2 +\cdots = \sum_{k=0}^{\infty} \frac{1}{k!} A^k\end{aligned} \]
と定義します。\(M_N\)は\(N\)次正方行列のなす集合です。\(e^A\)は、通常の指数関数と区別がつきにくいので、\(\mathrm{exp}A\)と書かれることもあります。行列の指数「関数」とは言いますが、\(e^A\)は行列であり、指数行列と呼ぶ方が適切でしょう。
行列の指数関数は、無限和、すなわち行列の極限によって定義されています。行列のなす空間\(M_N\)は、\(N^2\)次元の線形空間であり、
\[ \begin{aligned}\| A\| := \sqrt{ \sum _{i,j=1} ^N a_{ij} ^2}\end{aligned} \]
というノルム(フロベニウスノルム)を考えられます。このノルムによる極限が、行列の極限です。つまり、各成分ごとの極限を考えることに対応しています。行列の微分も同様に定義されます。
任意の正方行列\(A\)に対し、\(e^A\)は収束します。任意の正方行列はジョルダン標準形に変形でき、各成分を計算すれば\(e^t\)が収束することに帰着するので。
線形常微分方程式の解であること
線形常微分方程式\[ \begin{aligned}\frac{du}{dt}(t) = A u(t)\end{aligned} \]の解が、行列の指数関数を使って、\(u(t)= e^{tA} u_0\)と表されることを確かめてみましょう。
まず、\(e^{tA}\)の微分を計算してみます。
\[\begin{aligned} \frac{d}{dt}( \sum _{k=0} ^K \frac{1}{k!}t^k A^k) &=( \sum _{k=0} ^K \frac{k}{k!}t^{k-1} A^k) \\ &=( \sum _{l=0} ^{K-1} \frac{1}{l!}t^l AA^l) \\ &=A ( \sum _{l=0} ^{K-1} \frac{1}{l!}t^l A^l) \end{aligned} \]
なので、\(K\to \infty\)とすれば、\(\frac{d}{dt} e^{tA}= A e^{tA}\)です。よって、
\[\begin{aligned} \frac{du}{dt} &=\frac{d}{dt}(e^{tA} u_0) \\ &=\frac{d}{dt}(e^{tA} )u_0 \\ &= Ae^{tA}u_0 \\ &= Au\end{aligned} \]
と満たします。
また、\(u(0)=e^{0A}u_0 = Eu_0 = u_0\)で、初期条件を満たします。
\(f(u)=Au\)はリプシッツ連続なので、この微分方程式には解が一意に存在します(ピカール-リンデレフの定理。例えば柳田「常微分方程式論」を参照)。よって、\(u(t)= e^{tA} u_0\)は唯一の解であることが言えました。
実際は、\(u(t)= e^{tA} u_0\)は、もう少し式を変形した方が計算しやすいです。
\(P\)を\(A\)の固有ベクトルを並べてできる行列とし、\(P^{-1}AP =D\)と表されたとします。(\(D\)は対角行列、またはジョルダン行列)
ここで\(v= P^{-1} u\)と新たな変数を考えると、
\[ \begin{aligned}\frac{dv}{dt} = P^{-1} \frac{du}{dt}= P^{-1} Au \\ = P^{-1}AP v = Dv\end{aligned} \]
となるので、\(v(t) = e^{tD} v_0\)です。これを元の変数に戻せば、\(u(t)= Pv = Pe^{tD} P^{-1}u_0\)となりました。
\(e^{tA}=Pe^{tD} P^{-1}\)と変形できることになります。すると、\(P\)は固有ベクトルを並べただけ、\(e^{tD}\)は\(D\)が対角行列、またはジョルダン行列なので、非常に計算しやすいです。
行列の指数関数の簡単な例、性質
少しだけ、行列の指数関数の例、性質を紹介します。
\(A=(t)\)という\(1\times1\)行列のとき、\(e^A = e^t\)であり、行列の指数関数は実変数指数関数の一般化となっています。
2次の簡単な例を見てみましょう。対角行列のべき乗は、対角成分のべき乗となるので、
\[\begin{aligned} \mathrm{exp} \begin{pmatrix} a& 0\\ 0 & b \end{pmatrix} &= \begin{pmatrix} \sum _{k=0} ^\infty \frac{1}{k!} a^k& 0\\ 0 & \sum _{k=0} ^\infty \frac{1}{k!} b^k \end{pmatrix} \\ &= \begin{pmatrix} e^a& 0\\ 0 & e^b \end{pmatrix}\end{aligned} \]
となります。
\(A= \begin{pmatrix} 0& -\theta \\ \theta & 0 \end{pmatrix} ,\theta \in \mathbb{R}\)のときを考えてみましょう。
\(A^2= \begin{pmatrix} -\theta ^2& 0 \\ 0 & -\theta^2 \end{pmatrix} ,\quad A^3= \begin{pmatrix} 0& \theta ^3 \\ -\theta ^3 & 0 \end{pmatrix} \)
といったように、対角成分には偶数次の項、非対角成分には奇数次の項が出ながら、符号が交代していくので、
\[\begin{aligned} \mathrm{exp} \begin{pmatrix} 0& -\theta \\ \theta & 0 \end{pmatrix} &= \begin{pmatrix} 1- \frac{1}{2!}\theta ^2 +\frac{1}{4!}\theta ^4+\cdots & -(\theta -\frac{1}{3!}\theta ^3 +\frac{1}{5!}\theta^5 + \cdots)\\ \theta -\frac{1}{3!}\theta ^3 +\frac{1}{5!}\theta^5 + \cdots & 1- \frac{1}{2!}\theta ^2 +\frac{1}{4!}\theta ^4+\cdots \end{pmatrix} \\ &= \begin{pmatrix} \sum _{k=0} ^\infty \frac{(-1)^{k+1}}{(2k)!} \theta^{2k}& -(\sum _{k=0} ^\infty \frac{(-1)^{k}}{(2k+1)!} \theta^{2k+1} ) \\ \sum _{k=0} ^\infty \frac{(-1)^{k}}{(2k+1)!} \theta^{2k+1} &\sum _{k=0} ^\infty \frac{(-1)^{k+1}}{(2k)!} \theta^{2k}\end{pmatrix} \\ &= \begin{pmatrix} \cos \theta& -\sin \theta\\ \sin \theta & \cos \theta \end{pmatrix} \end{aligned} \]
と回転行列が得られました。
ここで紹介した他にも、
\(AB=BA\)ならば、\(\exp(A+B)=\exp A \exp B\)(前提は落とせない)
任意の行列に対し、\(e^A\)は正則。\(\det e^A = e^{\mathrm{tr}A}\)で、\((e^A)^{-1}=e^{-A}\)
\(P\)を正則行列として、\(A=PBP^{-1}\)ならば、\(e^A = P e^B P^{-1}\)
\(A\)の固有値を\(\lambda_1,\dots,\lambda_N\)とすると、\(e^A\)の固有値は\(e^{\lambda_1},\dots,e^{\lambda_N}\)
といった性質が成り立ちます。(例えば齋藤「線型代数入門」を参照)
今回紹介した行列の指数関数は、常微分方程式の解の挙動を調べる力学系理論に役立ちます。
線形常微分方程式\(\frac{du}{dt}= Au\)において、その行列の固有値の実部の符号は、定常解\(u=0\)の安定性の判別に役立ちます。
一般解である\(e^tA u_0\)は、行列\(A\)を対角化(またはジョルダン行列に変形)すれば、対角成分に\(e^\lambda t\)が並びます。オイラーの公式により、指数関数の実数部分はその大きさに、虚数部分は回転に影響するので、実数部分の符号が大事というわけです。
参考:線形微分方程式の解の安定性は「固有値」を調べればわかる
線形でない常微分方程式についても、線形化することで解の安定性を調べられるケースもあります。また、各固有ベクトルに対応する不変集合を調べるのが、安定・不安定・中心多様体の理論です。
参考:微分方程式の安定性を調べる「線形化」の方法とは?、不変集合、安定・不安定・中心多様体とは何か?
指数行列は、ほかにも、リー群・リー環の理論や、偏微分方程式・関数解析学における連続半群の理論にも役立ちます。
行列の指数関数は、線形代数の講義・教科書ではあまりメインとしては扱われないことが多いですが、身につければ役に立つと思いますよ。
木村すらいむ(@kimu3_slime)でした。ではでは。
朝倉書店
売り上げランキング: 140,975