どうも、木村(@kimu3_s+lime)です。
力学系理論における、不変集合、安定多様体、不安定多様体、中心多様体という概念を簡単に紹介します。
不変集合とは
力学系のようすを調べるときに、不変集合は重要です。
集合\(S\subset \mathbb{R}^N\)がベクトル場\(\dot{x} = f(x)\)において不変(invariant)であるとは、
任意の\(x_0\in S\)に対し、\(x_0\)を初期値とする解が任意の時間\(t\in \mathbb{R}\)で\(S\)に属し続けること \(x(t,x_0) \in S\)
です。
例えば、平衡解のみを集めた集合\(S\)は不変集合です。
力学系の性質を調べるときに平衡解が重要であったわけですが、それを一般化するのが不変集合と言えます。
時間\(t\geq 0\)に対しての条件ならば正の不変集合(positively invariant set)、時間\(t\leq 0\)に対しての条件のときは負の不変集合(negatively invariant set)と言います。
安定・不安定・中心部分空間とは
安定・不安定・中心多様体の話をする前に、線形の場合でその概念を考えてみます。
\(\dot{x} = Ax,x\in \mathbb{R}^N\)という線形方程式を考えます。この方程式には\(\bar{x}=0\)という平衡解があります。
行列\(A\)には重複込みで固有値が\(N\)個あるわけですが、解の挙動を左右するのは固有値の実部が負か、正か、0かどうかでした。
そこで、\(E^s\)を実部が負の固有値に対応する広義固有空間、\(E^u\)を実部が正の固有値に対応する広義固有空間、\(E^c\)を実部が0の固有値に対応する広義固有空間とします。これらを、安定部分空間(stable subspace)、不安定部分空間(unstable subspace)、中心部分空間(center subspace)と呼びます。
(固有値\(\lambda\)の広義固有空間\(W_\lambda\)とは、\(\lambda\)に対応する広義固有ベクトルの張る空間です。\(W_\lambda= \ker (A-\lambda I)^r,r\)は代数的重複度。参考:広義固有ベクトル – Wikipedia)
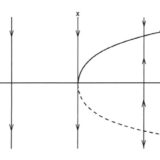
\(\mathbb{R}^2\)で具体例を見てみましょう。
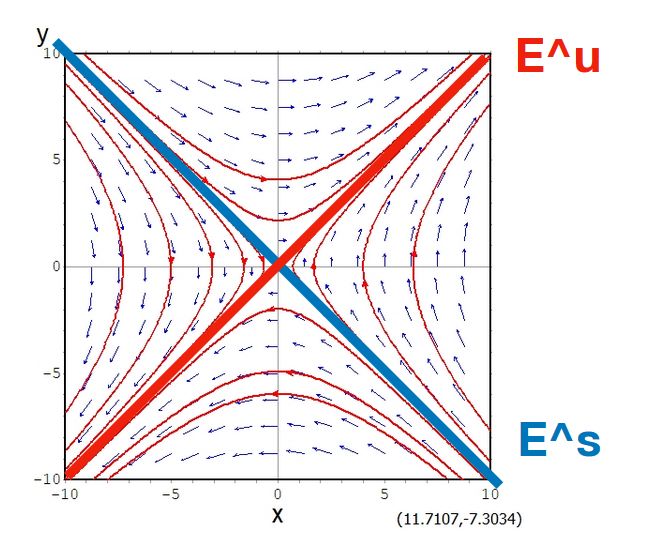
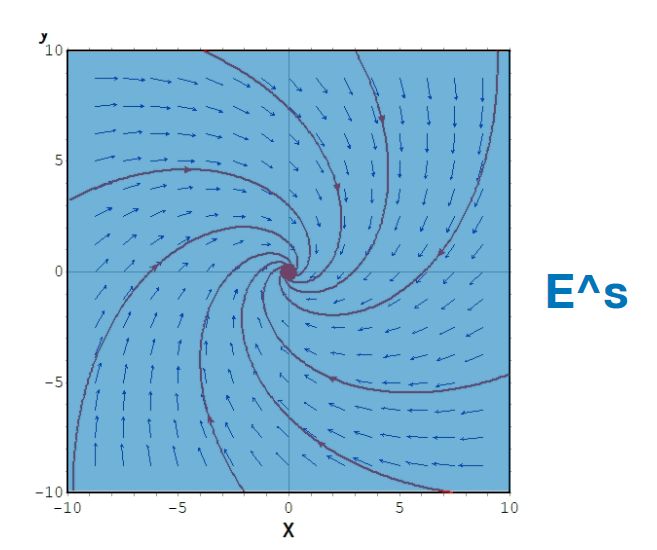

後者2つは自明(\(\mathbb{R}^2\))になっていますが、前者は\(E^s,E^u\)が分かれています。
\(x(0)\in E^s\)ならば\(\lim_{t\to \infty } x(t) =\bar{x}\)、\(x(0)\in E^u\)ならば\(\lim_{t\to -\infty } x(t) =\bar{x}\)という性質があり、解の挙動が把握しやすくなっています。
そして、\(A\)の固有ベクトルが張る空間なので、不変集合でもあります。
一般には、全体空間は安定、不安定、中心部分空間の直和に分解することができます。(任意の行列はジョルダン標準形に相似である、線形代数学の理論より)
\[ \begin{aligned}\mathbb{R}^N = E^s \oplus E^u \oplus E^c\end{aligned} \]
安定・不安定・中心多様体とは
安定・不安定・中心部分空間の概念を、線形とは限らない一般の方程式の場合に当てはめたのが、安定・不安定・中心多様体です。
安定・不安定・中心多様体の存在定理
少し記号の準備が長めです、具体例は後で紹介します。
\[ \begin{aligned}\dot{x} =f(x),x \in \mathbb{R}^N\end{aligned} \]という方程式を考え、不動点\(\bar{x}\)があるとします。
不動点が\(0\)に来るように変数変換\(y=x-\bar{x}\)して、\(y=0\)でテイラー展開すると、
\[ \begin{aligned}\dot{y} = Df(\bar{x})y + R(y)\end{aligned} \]
ここで\(R(y)=O(\|y\|^2)\)となります。
この線形化行列\(Df(\bar{x})\)をブロック対角行列となるように線形変換\(y= T(u,v,w)\)できます。
\[ \begin{aligned} \begin{pmatrix} \dot{u} \\ \dot{v} \\ \dot{w} \end{pmatrix}= \begin{pmatrix} A_s & O& O \\ O & A_u & O \\ O & O & A_c \end{pmatrix} \begin{pmatrix} u \\ v \\ w \end{pmatrix}\end{aligned} \]
\[ \begin{aligned}u=(u,v,w)\in \mathbb{R}^s \times\mathbb{R}^u \times\mathbb{R}^c, s+u+c=N\end{aligned} \]
このとき、次のように局所的にグラフ\(h\)で表せる多様体が存在します。
\[\begin{align} W^s _{loc}(0) &= \{u \in \mathbb{R}^N \mid v=h^s _v (u),w=h^s _w (u) \\ & Dh^s _v (0)=O,Dh^s _w (0)=O, \|u\| \text{ sufficiently small}\} \\ \end{align}\]
\[\begin{align} W^u _{loc}(0) &= \{u \in \mathbb{R}^N \mid u=h^u _u (v),w=h^u _w (v) \\ & Dh^u _u (0)=O,Dh^u _w (0)=O, \|v\| \text{ sufficiently small}\} \\ \end{align}\]
\[\begin{align} W^c _{loc}(0) &= \{u \in \mathbb{R}^N \mid u=h^c _u (w),v=h^c _v (w) \\ & Dh^c _u (0)=O,Dh^c _v (0)=O, \|w\| \text{ sufficiently small}\} \\ \end{align}\]
この多様体\(W^s _{loc}(0),W^u _{loc}(0),W^c _{loc}(0)\)をそれぞれ、(平衡解0に対する局所的な)安定多様体(stable manifold)、不安定多様体(unstable manifold)、中心多様体(center manifold)と呼びます。
(多様体の定義は長いので、多様体の本をあたってください。例えば、曲線や局面、局所的にグラフとして表せる集合は多様体です。)
これらの多様体は、点\(0\)で交わり、それぞれが線形近似の不変部分空間に接している不変集合です。
さらに、\(x(0)\in W^s _{loc}(0)\)ならば\(\lim_{t\to \infty } x(t) =\bar{x}\)、\(x(0)\in W^u _{loc}\)ならば\(\lim_{t\to -\infty } x(t) =\bar{x}\)という、引き込み、押し戻しの性質を持っています。
存在定理を要約すれば、非線形方程式では、線形方程式のときに存在していた安定・不安定・中心部分空間を曲げたような集合が不変となっているわけです。この定理は、中心多様体定理とも呼ばれます。
逆に、解の挙動によって、よりシンプルに安定多様体、不安定多様体を定義することもあります。
\[ \begin{aligned}W^s (\bar{x})= \{x(0)\in \mathbb{R}^N \mid \lim_{t\to \infty } x(t) =\bar{x}\}\end{aligned} \]
\[ \begin{aligned}W^u (\bar{x})= \{x(0)\in \mathbb{R}^N \mid \lim_{t\to -\infty } x(t) =\bar{x}\}\end{aligned} \]
(このように集合を定義したからといって、一般に多様体の構造を持つとは限りません。)
具体例
具体例を紹介して終わりたいと思います。
\[ \begin{aligned} \left\{ \begin{array}{l} \frac{dx}{dt} =x \\ \frac{dy}{dt} =-y+x^2 \end{array} \right.\end{aligned} \]
なる方程式を考えると、\((0,0)\)は平衡解です。
線形化すると、不変部分空間は\(E^s=\{x=0\},E^u =\{y=0\}\)となっています。
さらには、この方程式は積分曲線を求められてしまうので、安定多様体、不安定多様体を描くグラフを明示的に求められます。
すなわち、一般解は\(y(x)=\frac{x^2}{3} + \frac{c}{x}\)となり、
その定数\(c\)は、\(y=h(x),h(0)=h'(0)=0\)を満たすものを探します。すると、\(h(x)=\frac{x^2}{3}\)で、
\[ \begin{aligned}W^s(0,0)= \{x=0\}\end{aligned} \]
\[ \begin{aligned}W^u(0,0)= \{(x,y)\in \mathbb{R}^2 \mid y=\frac{x^2}{3}\}\end{aligned} \]
となります。
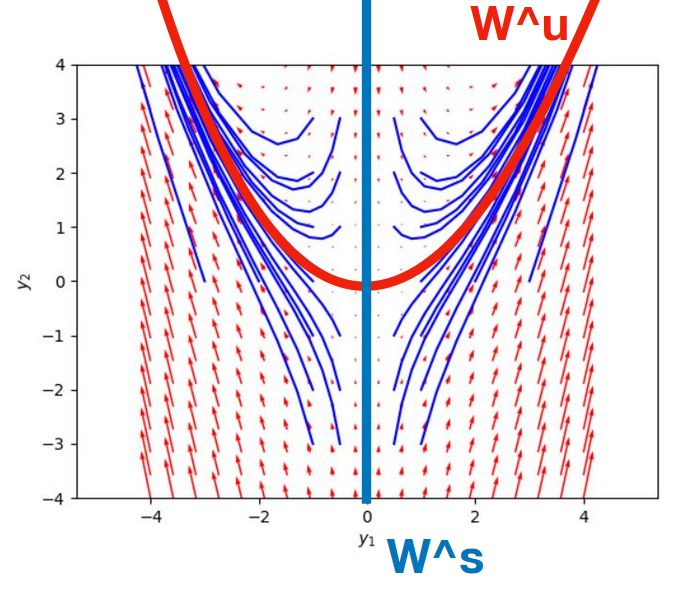
非線形方程式であっても、安定・不安定・中心多様体を調べれば、平衡解以外の挙動がどうなっているかもわかります。
正確には言えば、安定多様体と不安定多様体の挙動はわかりますが、中心多様体の挙動がどうなっているかはわかりません……(笑)。しかし、中心多様体を調べれば良いことになります。
パラメータによって系の挙動が変わる分岐現象を調べるときに、変数の数を中心多様体の次元まで減らして調べる方法として、中心多様体縮約と呼ばれるものがあります。
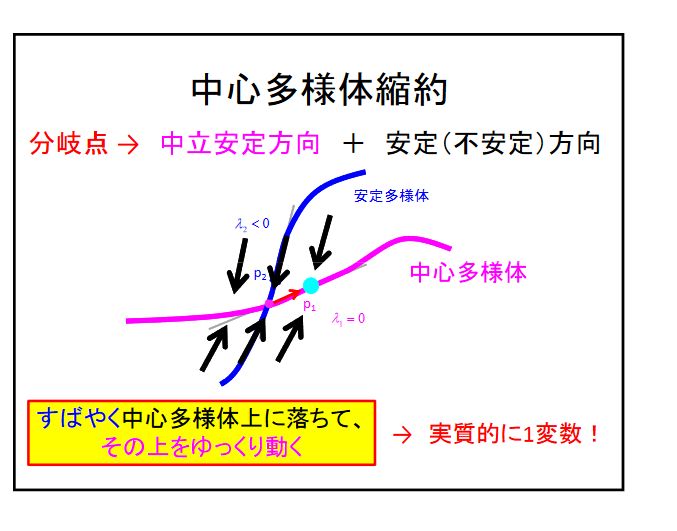
画像引用、参考:生命ダイナミクスを捉える:微分方程式 寺前順之介
偏微分方程式(無次元次元力学系)を調べるときにも、中心多様体上での軌道を有限次元まで落とせることがあります。
参考:反応拡散系に現れるカオス的挙動 – 北海道大学理学部数学科
力学系理論は、解の時間長期的な挙動を調べる学問であるわけですが、平衡解以外の特徴を調べる方法として、安定・不安定・中心多様体の理論が役立つでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Introduction to Applied Nonlinear Dynamical Systems and Chaos (Texts in Applied Mathematics)
Springer
売り上げランキング: 132,631
Springer (2010-12-08)
売り上げランキング: 160,125