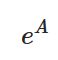どうも、木村(@kimu3_slime)です。
僕が線形代数学のアイデアとして面白いと思うことのひとつは、漸化式や線形常微分方程式を、線形空間、基底、固有ベクトルといった概念を使って解けることです。今回はそれを紹介します。
線形漸化式を解こう
フィボナッチ数列(Fibonacci sequence)は、うさぎの繁殖について考える数学モデルで、高校数学で扱うこともあるのではないでしょうか。それは、次のようにして定まる数列\(\{a_n\}_{n \in \mathbb{N}}\)です。
\[ \begin{aligned}a_{n+2} = a_{n+1}+a_n,\quad a_1=1,a_2=1\end{aligned} \]
前の二項を足し合わせたものによって、新たな次の項が決まる。そしてその項によって、次々と数の列が定まっていきます。このような数列に関する方程式を、漸化式(recursive formula)、または差分方程式(difference equation)と呼ぶのでした。
高校数学の範囲でも、「特性方程式を使えば解ける」という話を扱うかもしれませんが、なぜ特性方程式を使うと解けるのかは、わからないのではないでしょうか。今回は、それを線形代数学の立場から整理して説明します。
フィボナッチ数列を定める漸化式\(a_{n+2} = a_{n+1}+a_n\)は、線形漸化式、線形差分方程式です。
なぜかと言えば、方程式を満たす任意の数列\(\{a_n\},\{b_n\}\)と任意の定数\(c\)に対し、\(\{a_n+b_n\},\{c \cdot a_n\}\)も方程式を満たすからです。
\[\begin{aligned} a_{n+2} +b_{n+2} &= a_{n+1}+a_n + b_{n+1}+b_n \\ &= (a_{n+1}+b_{n+1})+(a_n + b_n) \end{aligned} \]
\[\begin{aligned} c\cdot a_{n+2} &= c(a_{n+1}+a_n ) \\ &= c\cdot a_{n+1}+ c\cdot a_{n} \end{aligned} \]
これは次のように言い換えられます。
\[ \begin{aligned}V:=\{\{a_n\} \mid a_{n+2} = a_{n+1}+a_n\}\end{aligned} \]
と集合を定め、\(V\)が線形空間(ベクトル空間)になるとき、その方程式を線形であると言います。方程式の解が定める線形空間\(V\)を、解空間(solution space)と呼びます。
与えられた線形空間に対し、必ず基底と呼ばれるベクトルの集合が存在し、その個数(次元)は一意に定まるのでした。
\(V\)は2次元です。\(d_1=1,d_2=0\)によって定まる数列を\(\{d_n\}\)、\(e_1=0,e_2=1\)によって定まる数列を\(\{e_n\}\)とすると、\(\{\{d_n\},\{e_n\} \}\)は基底なので。\(V\)の数列は、最初の2項の値のみによって決まるわけです。
目標は、解空間\(V\)のわかりやすい基底を得ることです。つまり、\(n\)によって明示的に表される基底を得たら、漸化式を満たす数列\(\{a_n\}\)はその線形結合として表されるわけですから。
今回、そのわかりやすい基底は、方程式から自然に定まる行列の固有値、固有ベクトルによって得られます。
数列の項を1つだけずらす写像\(T:V\to V\)を考えましょう。つまり、\(T(\{a_n\}):= \{a_{n+1}\}\)です。\(T\)は線形写像になります。
このシフト写像\(T\)は、基底\(\{\{d_n\},\{e_n\} \}\)によって行列として表現できます。
一般に、\(d_{n+1}=d_n +e_n\)、\(e_{n+1}= d_n\)という関係式が成り立っているので、
\[ \begin{aligned}T(\{d_n\},\{e_n\}) \\ =(\{d_{n+1}\},\{e_{n+1}\}) \\= (\{d_n\}+\{e_n\},\{d_n\}) \\= \begin{pmatrix} 1& 1\\1 &0 \end{pmatrix} \begin{pmatrix} \{d_n\}\\ \{e_n\} \end{pmatrix}\end{aligned} \]
と行列(\(A\)としましょう)によって表されます。これは漸化式
\[ \begin{aligned}\begin{pmatrix} a_{n+2}\\a_{n+1} \end{pmatrix}= \begin{pmatrix} 1& 1\\1 &0 \end{pmatrix} \begin{pmatrix} a_{n+1}\\a_{n} \end{pmatrix} \end{aligned} \]
に対応しているものです。
(\(W:= \mathbb{R}^2\)とし、\(\varphi : V\to W\)を\(\{a_n\}\mapsto (a_0,a_1)\)によって定めると、\(\varphi\)は全単射な線形写像、すなわち同型写像です。このとき、\(T_A: W\to W\)を\(Tx=Ax\)により定めると、\(T_A \circ \varphi = \varphi \circ T\)が成立しています。つまり、\(V\)と\(W\)を同一視、すなわち数列の最初の2項のみに注目することで、数列のシフト\(T\)は行列\(A\)と同一視できるわけです。)
仮に\(T\)の固有値・固有ベクトルが求まったとしましょう。
このとき、\(\{b_{n+1}\}=T(\{b_n\})= \lambda \{b_n\}\)なので、任意の\(n\)に対して\(b_{n+1}= \lambda b_n\)が成立しています。これを繰り返し用いれば、\(b_n = \lambda ^n b_1\)なので、固有ベクトルとなる数列の一般項が\(n\)によって表すことができるわけです。
そしてその固有ベクトルたちが\(V\)の基底になるならば、漸化式を満たす数列\(\{a_n\}\)の一般項を表すことができ、解が求まります。
\(T\)の固有ベクトルは、等比数列です。\(T\)の固有ベクトルを基底として\(W\)の元を表すことは、漸化式を満たす数列を等比数列の線形結合として表すことに対応しています。等比数列を定める漸化式は簡単に解けるので、そういう形に帰着させたいですね。
では、\(T\)の固有値・固有ベクトル、すなわち表現行列\(A\)の固有値・固有ベクトルを求めましょう。\(Ax = \lambda x\)を満たすような\(\lambda\)は、固有方程式、または特性方程式
\[ \begin{aligned}\mathrm{det} (A-\lambda E) =0\end{aligned} \]
によって求まるのでした。計算してみると、\(\mathrm{det} (A-\lambda E) = \lambda ^2 -\lambda -1\)なので、固有方程式を解けば
\[ \begin{aligned}\lambda = \frac{1\pm \sqrt{5}}{2}\end{aligned} \]
で、対応する固有ベクトルは、
\[ \begin{aligned}\begin{pmatrix} \frac{1\pm \sqrt{5}}{2} \\ 1 \end{pmatrix} \end{aligned} \]
です。これに対応する\(T\)の固有ベクトル、\(b_n =(\frac{1\pm \sqrt{5}}{2} )^n b_1\)を満たしています。
一般に、異なる固有値に対応する固有ベクトルは、互いに線形独立です。そして、\(V\)の次元は2なので、これらは基底でもあります。
よって、\(V\)の任意の要素、すなわち漸化式の解を、\(c_1,c_2\)を任意定数として
\[ \begin{aligned}a_ n = c_1(\frac{1+ \sqrt{5}}{2} )^n +c_2 (\frac{1- \sqrt{5}}{2} )^n \end{aligned} \]
と表すことができました。
特にフィボナッチ数列は、\(a_1=1,a_2=1\)を満たすものだったので、\(c_1,c_2\)が求められて
\[ \begin{aligned}a_ n = \frac{1}{\sqrt {5}}(\frac{1+ \sqrt{5}}{2} )^n -\frac{1}{\sqrt {5}} (\frac{1- \sqrt{5}}{2} )^n \end{aligned} \]
と一般項が求められました。
整数の数列ですが、一般項には無理数が含まれているのが面白いですね。その無理数は二次方程式に由来していますが、その二次方程式は漸化式が定める行列の特性方程式だったのです。
正の固有値\(\lambda = \frac{1+ \sqrt{5}}{2}\)は、黄金比に登場する数で、黄金数と呼ばれています。
まとめ・一般化
今回の話をまとめつつ、一般化してみましょう。
漸化式\(a_{n+r}+b_1 a_{n+r-1}+\cdots + b_n a_r =0\)によって定まる数列\(\{a_n\}\)を、最初の\(n\)項によって表したいという問題を考えます。
このとき、方程式は線形で、解空間\(V\)は\(n\)次元の線形空間になります。
数列を一つずらすシフト写像\(T\)を考えると、その特性方程式は
\[ \begin{aligned}\lambda ^n + b_1 \lambda^{n-1}+\cdots + b_{n-1} \lambda +b_n =0\end{aligned} \]
となります。
もしこれが重複する解を持たないならば、固有ベクトルたちは\(V\)の基底となります。シフト写像\(T\)の固有ベクトルとは、公比\(\lambda\)の等比数列なので、一般項が最初の\(n\)項によって求められます。
\[ \begin{aligned}a_n = c_1\lambda_1 ^n + c_ 2 \lambda_2 ^n +\cdots + c_n \lambda_n^n\end{aligned} \]
このとき、固有ベクトルを並べた行列を\(P\)とすると、
\(P^{-1} A P =\begin{pmatrix} \lambda_1 & 0 & \cdots&0 \\ 0 &\lambda_2& \ddots&\vdots \\ \vdots&\ddots &\ddots& 0 \\ 0& \cdots& 0 & \lambda_n \end {pmatrix} \)
と対角行列になるのでした(これを行列\(A\)の対角化という)。対角行列は、その\(n\)乗を簡単に計算できる(対角成分を\(n\)乗した行列になる)性質があります。したがって\(A^n\)が計算できるので、一般項が求められたわけです。
フィボナッチ数列の場合は重複する解を持ちませんでしたが、重複する解を持つ場合でも、工夫すれば一般解を求められます。対角化はできなくとも、\(A^n\)を計算しやすいような形にできれば良いわけです(対角化はできなくても、ブロック対角化はできる)。そのためには、広義固有空間、ジョルダン標準形の考え方が必要です。
漸化式は、多くの現象を表す常・偏微分方程式を、コンピュータにおいて離散的に解くときに登場します(差分法)。区間を\(n\)等分した解の近似列は、\(n\)項間の漸化式となり、線形代数の枠組みに収まります。
また、今回漸化式で議論したことは、線形常微分方程式でも同じように扱えます。
微分方程式\(x^{(n)}(t)+b_1 x^{(n-1)}(t)+\cdots + b_n x(t) =0\)によって定まる関数\(\{x(t)\}\)を、\(n\)個の初期値\(x^{(n)}(0),\dots,x(0)\)によって表す問題です。
解空間は\(n\)次元、シフト写像\(T\)は微分作用素\(x(t)\mapsto \frac{dx} {dt}(t)\)、等比数列に対応するのは指数関数\(e^{\lambda t}\)です。特性方程式を使った線形常微分方程式の一般解の求め方は、常微分方程式論の教科書や講義でも扱われます。
参考:2階線形常微分方程式を学ぶ意味:熱方程式への応用を例に
これまでの議論は、方程式が線形であるから有効なのでした。調べたい現象を表す漸化式・微分方程式が線形でない、すなわち非線形なときは、今回の議論は通用しません。非線形方程式を解くのは難しいですが、まずは線形方程式を解く方法を知っておくのが、大事な一歩でしょう。
フィボナッチ数列の一般項を得るという問題を、線形代数的なアイデア、解空間や基底、固有ベクトルといった概念によって解く方法を紹介しました。
線形代数学の重要な一般論として、線形空間、表現行列、固有値・固有ベクトル、対角化などがありますが、一般論だけ見ていても、それが何の役に立つのかは想像しにくいのではないでしょうか。
今回紹介したように、線形漸化式、線形常微分方程式の解法に役立つことがわかれば、一般論を学ぶモチベーションになるかと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
なぜ線形代数を学ぶ? Googleのページランクに使われている固有値・固有ベクトルの考え方