どうも、木村(@kimu3_slime)です。
今回は、条件付き極値問題とは何か、その解き方のひとつ、ラグランジュの未定乗数法を、幾何学的なイメージを重視して紹介します。
条件付き極値問題とは
例えば、「ある円に内接する四角形のうち、最大のものを求めよ」という問題は、条件付き極値問題と呼ばれます。
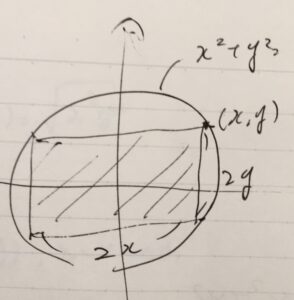
半径1の円\(x^2+y^2=1\)上の点\((x,y)\)を頂点とする四角形の面積は、\(f(x,y)=4xy\)となります。
\(g(x,y)=x^2+y^2- 1\)と置けば、\(g(x,y)=0\)が制約条件(constraint)です。\(g(x,y)=0\)を満たす条件のもとで、\(f(x,y)\)の極値が、条件付き極値(extremum for the function \(f\) subject to the constraint \(g\))と呼ばれます。
最適化問題の枠組みでは、\(f\)を目的関数と呼び、条件\(g\)のもとで\(f\)を最大・または最小にする\(x\)(最適解)を求めます。
ラグランジュの未定乗数法
条件付き極値問題において、極値点を探す方法として、ラグランジュの未定乗数法(Lagrange multiplier method)が知られています。
\(f,g\)を\(C^1\)級の関数とし、\(S\)を\(g=0\)の解のなす集合で、\(S\)上で\(\nabla g \neq 0\)とする。
さらに、\(p\)を\(S\)上における\(f\)の極値点とする。
このとき、実数\(\nabla\)で、\(\nabla f (p) = \lambda \nabla g(p)\) を満たすものが存在する。
\(\nabla f = \mathrm{grad} f =(f_x,f_y)\)は偏微分係数を並べたベクトルで、勾配ベクトルです。
証明は、陰関数定理を用います。ラング「続 解析入門」や杉浦「解析入門 Ⅱ」を参照してください。
さきほどの具体例\(f(x,y)=4xy\)、\(g(x,y)=x^2+y^2- 1\)を用いて、どういう主張なのか考えてみましょう。
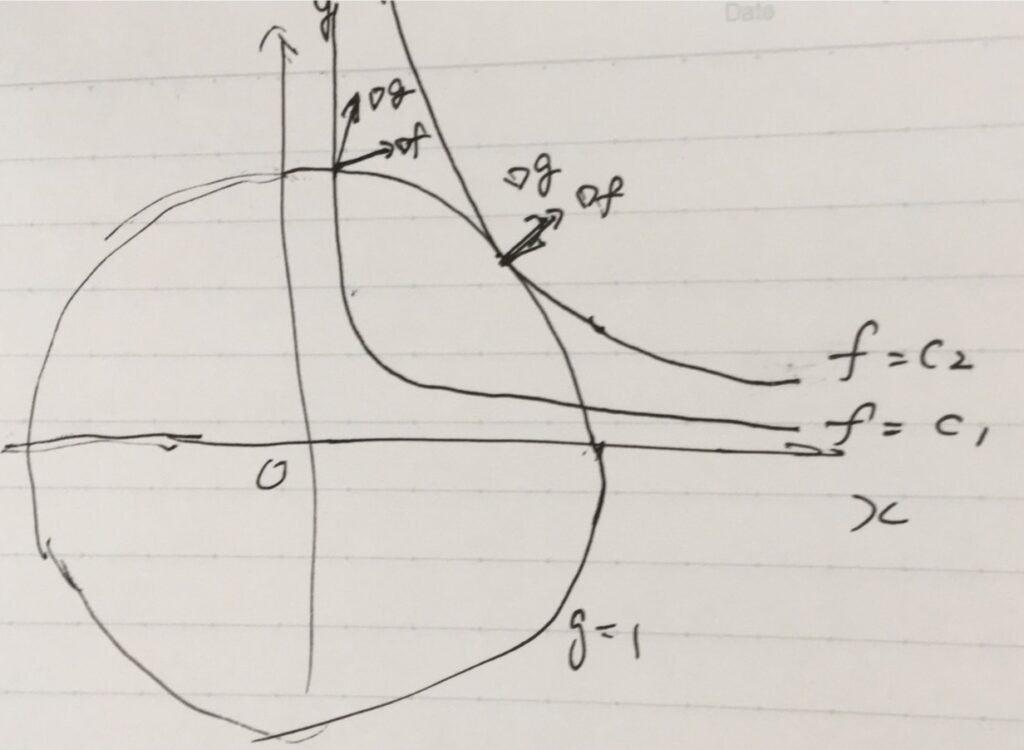
平面上に、\(f= c_1,f=c_2\)といった等高線を引いてみましょう。\(\nabla f =(4y,4x)\)は、\(f\)の増加する方向を向いています。\(\nabla g =(2x,2y)\)は、\(g\)の増加する方向、常に円の外側を向いています。
\(p \in S\)を\(f\)の\(S\)上の極値点とします。このとき、\(p\)を通る等高線\(f=c_2\)と\(g=0\)はちょうど接していなければならないでしょう。\(f=c\)において値\(c\)を連続的に変化させるとき、例えば大きな値から減少させていってはじめて\(g\)と交わるときは、グラフは接していなければなりません。
そのとき、\(z=f,z=g\)は空間において接平面を共有しています。すなわち、\(\nabla f (p) , \nabla g(p)\)が並行であること、つまり\(\nabla f (p) =\lambda \nabla g(p)\)なる\(\lambda\) の存在を示唆します。
逆に、\(f=c_1\)と\(g=0\)が接していないケースを考えます。その交点は極値点ではありえません。もし\(\nabla f(p),\nabla g (p)\)が並行でないならば、\(f\)をより増加・減少させる\(S\)上の点が存在するので、\(p\)は極値ではありません。
では、未定乗数法を使って、実際に極値点を求めてみます。
\(p=(x_0,y_0)\)を極値点とすると、未定乗数法により\(\nabla f (p) =\lambda \nabla g(p)\)を満たす\(\lambda\)が存在します。
つまり、\((4y_0,4x_0)= \lambda(2x_0,2y_0)\)です。2つの式から\(\lambda\)を消去すれば、\(x_0^2 =y_0^2\)が導かれます。制約条件\(g=0\)を使って\(y_0\)を\(x_0\)で表すと、\(x_0^2 =\frac{1}{2}\)です。
つまり、\(x_0 =\pm \frac{1}{\sqrt{2}}\)です。それぞれのケースについて、\(y_0 =\pm \frac{1}{\sqrt{2}}\)が得られます。
よって、極値点の候補は\((\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}),(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}),(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}),(-\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}})\)となりました。
ここで、\(S\)は有界な閉集合で、\(f\)はそこで連続なので、最大値・最小値の定理より\(f\)は\(S\)上で最大値・最小値を持ちます。したがって、以上の極値点の候補に、必ず最大点・最小点が含まれています。(有界な閉集合については別記事で紹介予定)
実際に\(f\)の値を比較すれば、次のことがわかります。\((\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}),(-\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}})\)が最大点で、最大値は\(2\)。\((-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}),(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}})\)が最大点で、最小値は\(-2\)。
以上によって、半径1の円に内接する四角形のうち、面積を最大にするものは正方形であり、最大値は\(2\)であることがわかりました。
ちなみに、\(g=0\)の制約条件がなければ、\(f(x,y)=4xy\)は極値を持ちません。条件のないケースで極値点は、\(\nabla f(p_0)=0\)を満たします。\((0,0)\)が極値点の候補として唯一見つかりますが、付近で値は増減するので極値点ではありません。
勾配=0で極値を求めるときも、ラグランジュの未定乗数法も、極値点の候補を見つけているにすぎないことに注意しましょう。候補が見つかったら、実際にそれが極値点であるかどうか判別する必要があります。
ただし、未定定数法において、(円のように)定義域が有界閉集合なときは、最大値・最小値をそこで持つことが一般論によりわかるので、候補点の比較で極値が求められるわけです。定義域が非有界なときは、陰関数を使って極値点であるかどうかを実際にチェックする必要が出てきます。
以上、条件付き極値問題とラグランジュの未定乗数法を紹介してきました。
今回紹介した例を少し変えれば、円や楕円に内接する三角形や多角形、球に内接する立方体や多面体、その面積や体積を最大にする問題は、条件付き極値問題です。これらは、ラグランジュの未定乗数法によって解くことができます。また、\(f\)が3変数以上の関数で、制約条件\(g\)が複数あるケースでも、同様の手法が成り立ちます。
未定乗数法は、最適化問題、ミクロ経済学、解析力学、統計力学などでも利用されるようです。極値を求める問題に出会ったら、ぜひ未定乗数法を思い出してみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1981-11-15T00:00:01Z)
¥5,720
東京大学出版会 (1985-04-25T00:00:01Z)
¥3,740