ユークリッド空間の開集合、閉集合、開球、近傍とは何か？

どうも、木村（@kimu3_slime）です。

今回は、ユークリッド空間の開集合、閉集合、開球、近傍といった考えについて、具体例を挙げながら解説します。

開区間と閉区間
開球、近傍とは
開集合、閉集合とは
有界閉集合上の連続関数
こちらもおすすめ

開区間と閉区間

まず、実数\(\mathbb{R}\)における開区間、閉区間の定義を思い出しましょう。\(a,b\in\mathbb{R}\)として、

\[ \begin{aligned}(a,b)= \{x\in \mathbb{R} \mid a<x<b\}\end{aligned} \]

\[ \begin{aligned}[a,b]= \{x\in \mathbb{R} \mid a\leq x\leq b\}\end{aligned} \]

これらをそれぞれ、開区間（open interval）、閉区間（closed interval）と呼びます。

参考：集合論入門：集合の定義、数の集合、ラッセルのパラドックス

例えば、\(f(x)=\frac{1}{x}\)という関数を考えましょう。定義域を\([1,2]\)とすれば、\(f\)は連続であり、最大値と最小値を持っています。

この関数は\(x=0\)の場合は、定義されないと考えることもあるでしょう。ただし、\(f(0)=0\)と仮に定義することで、\(0\)を含む区間で定義された関数と考えることができます。

この\(f\)は、\([-1,1]\)において連続ではありません。\(\lim _{x\searrow 0}\frac{1}{x}= \infty\)であるからです。そして、\([-1,1]\)において\(f\)は最大値、最小値を持ちません。

また、\((0,\infty)= \{x\in \mathbb{R} \mid 0<x\}\)という無限区間を考えると、\(f\)は連続ではありますが、最大値、最小値を持ちません。\(f\)は限りなく大きな値を取り、限りなく0に近い値を取りますが、決してそれを区間\((0,\infty)\)において実現することがないのです。

このように、関数の連続性（や極限）、最大値・最小値を持つかといった性質を考えるときに、開区間や閉区間の考え方が必要になってきます。

開球、近傍とは

ここまで実数直線\(\mathbb{R}\)を考えてきましたが、平面\(\mathbb{R}^2\)や空間\(\mathbb{R}^3\)、より一般にユークリッド空間\(\mathbb{R}^N\)を舞台として考えたいです。それにより、2変数関数、多変数関数の定義域を考えることができます。

開区間や閉区間といったものを一般化するために、まず開球という考え方を導入します。

\[ \begin{aligned}B_N (a,r)= \{ x\in \mathbb{R}^N \mid \|x-a\|<r \}\end{aligned} \]

を、点\(a \in \mathbb{R}^N\)を中心とする半径\(r>0\)の\(N\)次元の開球（open ball）と呼びます。ここで\(\|x\|\)は\(x\)のノルム（大きさ）です。

例えば、1次元の開球は\(B_1(0,r)= (-r,r)\)という開区間。2次元の開球は、\(B_2(0,r)=\{ (x,y)\in \mathbb{R}^2 \mid \sqrt{x^2+y^2}<r \}\)という開円盤（open disc）です。\(B_3(0,r)=\{ (x,y,z)\in \mathbb{R}^2 \mid \sqrt{ x^2+y^2+z^2}<r \}\)は、まさに開いた球となります。\(N\)が文脈上明らかであるときは、\(B(a,r)\)と次元が省略して書かれることがあります。

幾何学なイメージにかかわらず、1点\(a\)から距離\(r\)以下の点\(x\)を集めた集合を、（何次元であっても）開球と呼ぶことにしましょう。

\(x\)を中心とする開球は、\(x\)の近くの点をすべて含みます。

そこで、部分集合\(V\subset \mathbb{R}^N\)が、開球\(B(x,r)\subset V\)を含むとき、\(V\)を\(x\)の近傍（neighbourhood）と呼ぶことにします。

例えば、\(B(a,r)\)は\(a\)の近傍です。このように開集合であり近傍であるものは、開近傍とも呼ばれます。また、\([a-1,a+1]\)も\(a\)の近傍です（確かめてみてください）。

関数\(f\)の\(p=p_0\)におけるテイラー展開は、\(p_0\)の「まわりで」成立します。この小さいかもしれないが一定の大きさを持った範囲を、近傍と呼び、「\(x=a\)の近傍でテイラー展開できる」といったように言うわけです。

開集合、閉集合とは

いよいよ、部分集合\(U \subset \mathbb{R}^N\)が開集合、閉集合とはどういうことか、定義しましょう。

\(U \)が開集合（open set）であるとは、各点\(x\in U\)に対して、半径\(r>0\)を小さく取れば、\(x\)を含む開球が\(U\)に含まれる\(B(x,r)\subset U\)ことです。

\(U \)が閉集合（closed set）であるとは、補集合\(\mathbb{R}^N \backslash U \)が開集合となることです。

全称命題や存在命題の否定を思い出すと、\(U\)が開集合でないとは、ある点\(x\in U\)で次を満たすものが存在することです。任意の\(r>0\)に対して、\(B(x,r)\not \subset U\)である。

（開集合、閉集合には、いろいろな同値な定義が知られています）

1次元の例

1次元のケースで、開集合や閉集合の例を見てみましょう。

開区間\((a,b)\)は開集合です。

なぜか。まず、\(x\in (a,b)\)を任意に取ります。半径としては\(x\)から端っこ\(a,b\)までの距離より小さく、例えば\(r:= \min \{\frac{x-a}{2},\frac{b-x}{2} \}\)としましょう。そして、\(B(x,r) \subset (a,b)\)を示します。\(y \in B(x,r)\)とすると、\(|y-x|<r\)、\(-r <y-x <r\)、\(-r+x <y <r+x\)です。\(r<\frac{x-a}{2}\)より、\(-r+x\geq -\frac{x-a}{2}+x=\frac{x}{2}+\frac{a}{2}> \frac{a}{2}+\frac{a}{2}=a\)となります（\(a<x\)に注意）。同様にして、\(r<\frac{b-x}{2}\)より、\(r+x<b\)です。よって、\(a<y<b\)であり、\(y\in (a,b)\)です。よって、\((a,b)\)は開集合であることが示せました。

閉区間\([a,b]\)は閉集合です。

補集合は\(\mathbb{R}\backslash [a,b] =\{x\in \mathbb{R} \mid x<a または b<x\}=(-\infty ,a)\cup (b,\infty)\)です。さきほどの議論と同様にして、\((-\infty ,a), (b,\infty)\)は開集合です。そして、その和集合\((-\infty ,a)\cup (b,\infty)\)もまた開集合となります。\(x\in(-\infty ,a)\cup (b,\infty) \)を取れば、\(x\)はいずれにせよ開集合に含まれる点なので、適切な開球を持つからです。よって、補集合が開集合なので、閉区間\([a,b]\)は閉集合と言えました。

すべての部分集合が、開集合または閉集合のいずれかに分類されるわけではないことに注意しましょう。

半開区間\((a,b]\)は開集合でも閉集合でもありません。

開集合かどうか考えると、端点\(b\)でおかしなことが起こっていそうです。\(b\)を含む開球は、必ず\((a,b]\)の外側に出てしまいます。半径\(r\)を任意にとって、\(B(b,r)\)を考えましょう。すると、\(b+\frac{r}{2} \in B(b,r)\)です。しかし、\(b+\frac{r}{2} >b\)なので、\(b+\frac{r}{2} \not \in (a,b]\)です。よって、\(B(b,r) \not \subset (a,b]\)となり、開集合ではないことが示せました。

補集合\(\mathbb{R} \backslash (a,b]\)が開集合かどうか考えると、端点\(a\)で同様の議論を行って、開集合でないことが示せます。よって、\((a,b]\)は閉集合でもありません。

全体集合\(\mathbb{R}\)は、開集合であり、閉集合でもあります。

任意の点を選んでどんな半径の開球を考えても、それは\(\mathbb{R}\)に必ず含まれるので、\(\mathbb{R}\)は開集合です。また、補集合は空集合\(\varnothing\)ですが、空集合は開集合です。一般に、命題P⇒Qの真偽は、仮定Pが偽のとき、Qの真偽によらず常に真になります（空真、空ゆえに真）。\(x \in \varnothing\)という仮定は成り立たないので、開集合の定義後半の主張は真となり、空集合は開集合というわけです。

内点、境界

開集合や閉集合の幾何学的なイメージを捉えるために、内点、境界といった用語もよく使われます。

\(U\)を一般の部分集合\(U \subset \mathbb{R}^N\)としましょう。

\(x\in U\)が\(U\)の内点（interior point）であるとは、\(x\)を含む開球で\(U\)に含まれるものが存在することです。

\(x\in \mathbb{R}^N\)が\(U\)の境界点（boundary point）であるとは、\(x\)を含む任意の開球が、\(U\)とも\(U\)の補集合とも共通部分を持つことです。（この定義では、\(x\in U\)でなくても良いことに注意）

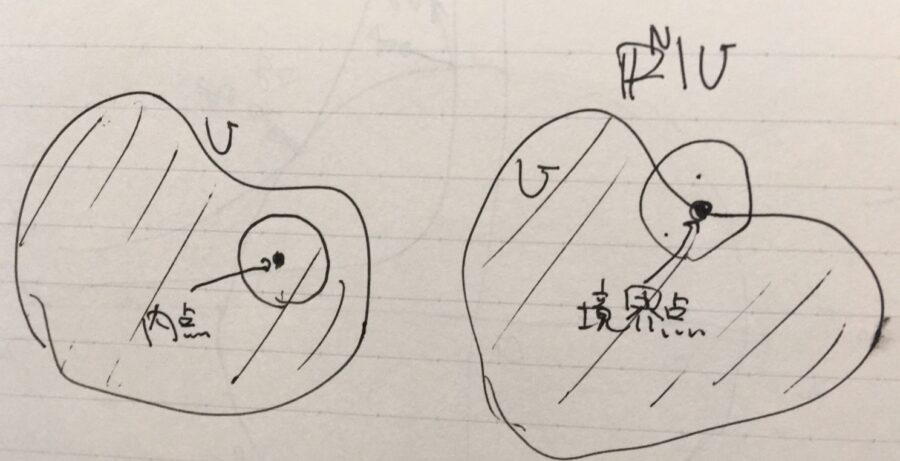
\(U:=(a,b]\subset \mathbb{R}\)としましょう。

さきほどの議論によって、\(b\in U\)は\(U\)の内点ではありません。境界点ではあります。\(U\)の内点全体の集合は、開区間\((a,b)\)であり、開集合となっています。開集合とは、内点のみからなる集合と言えます。（一般の部分集合に対し、その内点の集合を内部という）

また、\(U\)の境界点は、\(a,b\)のみです。\(U\)に境界点を加えた集合は、\(U\cup {a,b}=[a,b]\)と、閉区間になります。閉集合とは、境界点をすべて含む集合と言えます。（一般の部分集合に対し、その境界点との和集合を閉包という）

2次元の例

1次元のイメージがつかめてきたので、2次元の例を考えましょう。

\(B_2(a,r)\)は、開集合です。

任意に\(p_0\in B_2(a,r)\)を取ります。\(s= \frac{r-\|p_0-a\|}{2}>0\)としましょう。\(B_2 (p_0,s)\subset B_2(a,r)\)が示せます。\(p\in B_2 (p_0,s)\)とすると、\(\|p-p_0\|<s\)です。三角不等式より、

\[ \begin{aligned} \|p-a\| & \leq \|p-p_0\|+\|p_0-a\|\\ &<&\frac{r-\|p_0-a\|}{2} +\|p_0-a\| \\ &<&\frac{r}{2}+\frac{r}{2}=r \end{aligned} \]

なので、\(p \in B_2(a,r)\)であり、\(B_2(a,r)\)が開集合であることが示せました。

\(D_2(a,r) = \{ x \in \mathbb{R}^2 \mid \|x-a\|\leq r\}\)や\(S^1 = \{x \in x \in \mathbb{R}^2 \mid \|x-a\|= r\}\)は閉集合です。

その補集合が開集合であることは、さきほどの議論と同様にして示せます。

境界点の議論からも、閉集合であることがわかります。例えば、\((1,0)\in \mathbb{R}^2\)は、\(B_2(a,r)\)の境界点です。\(B_2(a,r)\)の境界点全体の集合は、\(S^1 \)に他なりません（確かめてみてください）。したがって、境界点すべてを加えた和集合\(D_2 (a,r) = B_2 (a,r) \cup S^1\)は、閉集合となっています。

開区間同士、閉区間同士の直積集合\((a,b)\times(c,d)\)や\([a,b]\times[c,d]\)は、それぞれ開集合、閉集合です。

以上の議論は、2次元でなく、一般の次元\(N\)でも成り立ちます。

有界閉集合上の連続関数

微積分学において、開集合や閉集合は、一般論を厳密に組み立てるために有効です。

例えば、平均値の定理では、関数は閉区間\([a,b]\)で連続、開区間\((a,b)\)で微分可能という仮定が置かれます。値が連続的に変化しているかどうかを考える時は、端点\(a,b\)を含めるのが自然です。一方で、微分可能性を考える時は、その点の近傍での極限を考えるので、開集合を考えることになります。

また、「有界な閉集合上で連続な関数は、最大値・最小値を持つ」という最大値・最小値の定理は、微積分学の基礎です。

部分集合\(U\subset \mathbb{R}^N\)が有界（bounded）であるとは、ある大きな半径\(R>0\)によって\(U\)が開球に含まれる\(U \subset B_N(0,r)\)と定義されます。

例えば、閉区間\([a,b]\)や円周\(S^1\)は有界です。一方で、\((0,\infty)\)や\(\{(x,y)\mid x=y\}\)は有界ではありません。有界な集合とは、およそ「有限の大きさ」を持った集合と言えるでしょう。

冒頭で考えた関数\(f(x)=\frac{1}{x}\)は、最大値・最小値を定義域によって持ったり持たなかったりしましたが、その違いは、有界な閉集合上で連続かどうか、という点にあったわけです。

また、多変数関数の条件付き極値問題を考えるとき、定義域が有界な閉集合ならば、そこで最大値・最小値を持つことが一般論として保証されます。

有界な閉集合は、位相空間論において、コンパクトな集合として一般化されます。コンパクト集合上の連続関数は、最大値・最小値を持つ。これは別の記事で紹介予定。

以上、ユークリッド空間の開集合、閉集合、開球、近傍について、具体例を挙げながら解説してきました。

微積分学の基礎的な議論や、位相空間論への入門として、これらの扱いに慣れると良いでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。