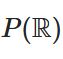どうも、木村(@kimu3_slime)です。
今回は、連続関数、可積分関数のなす線形空間、微分と積分の線形性について、簡単に解説します。
連続関数のなす線形空間
連続関数のなす集合は\(C^{0}\)、連続微分可能な関数のなす集合は\(C^1\)と表す、といった話を以前紹介しました。
実は、それらは(抽象)ベクトル空間・線形空間の枠組みを満たします。関数も、一種の「ベクトル」としての性質を持つのです。
\(U\)をユークリッド空間\(\mathbb{R}^N\)の開集合とします。
\[ \begin{aligned}C^0(U) = \{f:U\to\mathbb{R} \mid f は連続\}\end{aligned} \]
\[ \begin{aligned}C^k(U) = \{f:U\to\mathbb{R} \mid f はk 回微分可能で、f^{(k)}は連続\}\end{aligned} \]
\[ \begin{aligned}C^\infty(U) = \{f:U\to\mathbb{R} \mid f は何回でも微分可能\}\end{aligned} \]
これらが線形空間の条件を満たすことを確かめましょう。特に、\(V:=C^0(U) \)について考えます。
\(V\)を集合とする。次の条件が、\(V\)は線形空間であることの定義。
\(V\)の任意の要素\(x,y,z\)、任意の数\(a,b\in \mathbb{R}\)に対し、和\(x+y \)、スカラー乗法\(ax \)と呼ばれる\(V\)の要素が定まり、次の条件を満たす。
結合法則:\((x+y)+z = x+(y+z)\)
交換法則:\(x+y =y+x\)
ゼロベクトルの存在:\(\exists o(o+x =x)\)
逆ベクトルの存在:\(\exists w (x+w=o)\)。これを逆ベクトルと言い、\(w=-x\)と書く。
分配法則:\((a+b)x= ax+bx\)
分配法則:\(a(x+y)=ax+ ay\)
両立条件:\((ab)x= a(bx)\)
スカラー乗法の単位要素:\(1x =x\)
まず、関数同士の和とスカラー乗法が定まる必要があります。
\(f,g \in C^0(U)\)、\(a\in \mathbb{R}\)に対して、
\[ \begin{aligned}(f+g)(x) = f(x)+g(x)\end{aligned} \]
\[ \begin{aligned}(af)(x) = a f(x)\end{aligned} \]
と、関数の和\(f+g\)、スカラー乗法\(af\)を定めます。それぞれ、関数としての値を足すこと、定数倍することで、新しい関数を生み出しているわけです。
連続関数の和と、スカラー乗法は、また連続関数となります。
\[ \begin{aligned}\lim _{x\to p} (f+g) (x)= \lim_{x\to p}f(x)+\lim_{x\to p}g(x)\\ = f(p)+g(p)=(f+g)(p)\end{aligned} \]
\[ \begin{aligned}\lim _{x\to p} (af) (x)= a\lim_{x\to p} f(x)\\ = a f(p)= (af)(p)\end{aligned} \]
ここで用いているのは、
\[ \begin{aligned}\lim _{x\to p} (f+g) (x)= \lim_{x\to p}f(x)+\lim_{x\to p}g(x)\end{aligned} \]
\[ \begin{aligned}\lim _{x\to p} (af) (x)= a\lim_{x\to p} f(x)\end{aligned} \]
という極限の性質です。これは極限の線形性と呼ばれ、厳密な定義から証明することができます。(関数でなく数列、点列に対しても成り立つ)
結合法則、交換法則、分配法則、両立条件、スカラー乗法の単位要素は、関数の値\(\mathbb{R}\)が持つ性質なので、そこから連続関数\(V\)も満たすことになります。
ゼロベクトルとしては、\(g_0(x)=0\)という恒等的に0になる関数が選べます。この\(g_0\)は、任意の\(f\in V\)に対して、\((f+g_0)(x)=f(x)+g_0(x)= f(x)+0=f(x)\)を満たすので、\(g_0+f=f\)を満たします。
逆ベクトルとしては、\(f\in V\)に対して、\(-f \in V\)が選べます。\((-f +f)(x) = -f(x)+f(x) =0 =g_0(x)\)なので、\(-f +f=g_0\)が成り立っているわけです。
単に記号として、\(-f+f= 0\)と操作できるわけではないことに注意しましょう。さきほどの関数の和、スカラー倍の定義を用いて、\(-f+f= 0\)が成り立つことを証明しました。一旦線形空間であることを示せれば、\(-f+f=0\)とベクトルの和を計算して良いですが、それを示すときには定義に立ち返らなければなりません。
以上によって、\(V:=C^0(U) \)が線形空間であることが示せました。\(C^k(U),C^\infty(U)\)についても同様です。
可積分関数のなす線形空間
連続関数や微分可能関数のなす集合が線形空間であったように、積分できる関数のなす集合も線形空間をなします。
\[ \begin{aligned}L^1 (U ):=\{f:U\to\mathbb{R} \mid \int_U |f(x)| dx <\infty \}\end{aligned} \]
\[ \begin{aligned}L^p (U ):=\{f:U\to\mathbb{R} \mid \int_U |f(x)|^p dx <\infty \}\end{aligned} \]
それぞれ、可積分関数のなす集合、\(p\)乗可積分関数のなす集合です(\(0<p<\infty\))。
この表記をするとき、普通はルベーグの意味での積分を考えますが、リーマンの意味での積分(高校までで学ぶ積分)として見ても、線形空間をなすことについては同様です。
\(L^{p}(U)\)は線形空間となります。
関数の和、スカラー倍は、連続関数と同様です。\(f,g \in L^{p}(U)\)とすると、
\[ \begin{aligned}(\int_U |f+g(x)|^p dx)^{\frac{1}{p}}\leq (\int_U |f(x)|^p dx)^{\frac{1}{p}}(\int_U |f(x)|^p dx)^{\frac{1}{p}} <\infty\end{aligned} \]
\[ \begin{aligned}\int _U (a f)(x)dx =a \int _U f(x)dx<\infty\end{aligned} \]
が成り立つので、\(f+g,af \in L^p(U)\)です。前半は、積分の三角不等式と呼ばれる性質です(ここでは証明しません。例えば、ルベーグ積分入門や関数解析を参照)。
その他の性質は、連続関数のときと同様にして示されます。よって、\(L^p(U)\)は線形空間です。
連続関数や可積分関数など、関数のなす線形空間は、一般に関数空間(function space)と呼ばれます。
微分の線形性
関数に対してその導関数を対応させる規則は、線形写像となっています。
\(V,W\)を線形空間とする。写像\(f:V\to W\)が線形写像(linear mapping)であるとは、次の条件を満たすこと。
(1) 加法性:任意の\(x,y \in V\)に対し、\(f(x+y)= f(x)+f(y)\)
(2) 斉次性:任意の数\(c\)に対し、\(f(cx) =cf(x)\)
\(D:C^1(U)\to C^0 (U)\)を、
\[ \begin{aligned}Df (x)= \frac{\partial f}{\partial x_k}(x)\end{aligned} \]
により定めます。(\(x_k\)方向の偏微分です。\(N=1\)ならば、単なる微分\(f^{\prime}\)です。)
\(D\)は線形写像になります。上の定義文における\(f\)は\(D\)に、ベクトル\(x,y\)は関数\(f,g\)に対応していることに注意しましょう。
\[ \begin{aligned}D(af+g)(x)= \frac{\partial (af+g)}{\partial x_k}(x)\\=\frac{\partial (af)}{\partial x_k}(x)+\frac{\partial g}{\partial x_k}(x)=a\frac{\partial f}{\partial x_k}(x)+\frac{\partial g}{\partial x_k}(x)\\ = aD(f) (x)+D(g)(x)\end{aligned} \]
微分の和や定数倍が取り出せるのは、極限の線形性によるものです。よって、\(D(af+g)= aD(f) (x)+D(g)\)が成り立つので、\(D\)は線形写像です。
関数空間における微分により定まる線形写像\(D\)は、微分作用素(differential operator)と呼ばれます。
積分の線形性
関数に対して、その積分値を対応させる規則もまた、線形写像となります。
\(I:L^1 (U)\to \mathbb{R}\)を、
\[ \begin{aligned}I(f) =\int_ U f(x)dx\end{aligned} \]
と定めます。すると、\(f,g \in L^1(U)\)に対して、
\[ \begin{aligned}I(af+g)= \int_U (af+g)(x) dx \\=\int_U af(x) dx+\int_U g(x) dx= a\int_U f(x) dx+\int_U g(x) dx \\ =aI(f)+I(g)\end{aligned} \]
が成り立ちます。これは、和と極限(上限)が線形性を持つことから、積分が線形性を持つという基本的な性質によるものです。よって、\(I\)は線形写像です。
関数空間から実数への線形写像\(I:L^1 (U)\to \mathbb{R}\)は、線形汎関数(linear functional)と呼ばれます。
(また、関数に対して、積分によって定まる関数を対応させる対応は線形写像であり、それは積分作用素と呼ばれます。)
以上、連続関数、可積分関数のなす線形空間、微分と積分の線形性について、簡単に紹介してきました。
今回は関数の定義域、行き先は実数\(\mathbb{R}\)とその部分集合を考えましたが、複素数でも、一般のノルム空間でも良いです。
実は、関数空間\(L^2\)では、\(\{\cos 0x, \cos kx, \sin kx\}_{k=1}^{\infty}\)といった関数が良い基底(正規直交基底)になっています。これはフーリエ級数の理論の基礎です。そのためには、関数空間に適切なノルムや内積を与える必要がありますが、それは別記事で紹介予定。
\(\mathbb{R}^N\)のベクトルや行列\(A\)だけでなく、関数のなす集合\(C^k(U),L^{p}\)や微分や積分が、線形空間、線形写像という枠組みでは共通していることを、感じてもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
遊星社 (2006-05-01T00:00:01Z)
¥4,290
共立出版 (1980-11-01T00:00:01Z)
¥5,390
こちらもおすすめ
線形代数の応用:関数の「空間・基底・内積」を使ったフーリエ級数展開