どうも、木村(@kimu3_slime)です。
「AならばBである」という文章は、日常会話では単に「Bである」と読み取られやすいです。これはよくある誤解と言っていいでしょう。
今回は、「AならばB」の論理学的な意味を確認してみましょう。
「もし」Aが正しいならば、Bも正しい
「資本主義が無条件に格差を拡大するならば、資本主義はやめたほうがよい」という命題を考えましょう。
これは単に「資本主義はやめたほうがよい」と言っているわけではありません。
しかし、普通に考えて、いまの世界はほんとおかしい。王族が富を独占していた時代に戻っている。民主主義とか資本主義とかいって仕組みを変えても、同じことが起こっている。
— 東浩紀 Hiroki Azuma (@hazuma) July 12, 2018
じゃあ資本主義と民主主義やめたほうがいいですね。 https://t.co/EegAt7QX1D
— 東浩紀 Hiroki Azuma (@hazuma) July 12, 2018
「資本主義は無条件に格差を拡大する→それならば資本主義はやめたほうがよい」という命題は、資本主義をやめろという命題と等価ではなく、「資本主義をやめたくないならば→資本主義は格差を無条件に拡大しないようにせよ」という命題と等価。論理学学んだほうがいいよ。
— 東浩紀 Hiroki Azuma (@hazuma) July 12, 2018
そういうことではありません。論理を大切にしましょう。 https://t.co/J69yOjGrQu
— 東浩紀 Hiroki Azuma (@hazuma) July 12, 2018
「AならばB」とは、論理学では、Aという前提条件が正しいならば、Bも正しいと言えるという主張です。
Aという条件抜きにBが正しいとは一言も言っていないのです。
「(CであろうがDであろうが)Bである」とか「AでなくてもBである」とかいうのは、文に書かれていないことを読んでしまっている、読み取りすぎです。
論理学は、書かれていることを読み取り、書かれたこと以上のことを勝手に読み取らないための考え方を提供してくれます。人間にありがちな恣意的な解釈を減らし、お互いの誤解を減らすのに役立ちますね。
ツイッターやって10年ぐらい経つけど、ほんと、「じゃあ(それならば)」という条件付きの主張を理解できないひとが多いね。これ国語教育にも問題あるんじゃないかな。「AならばBだ」と書くと「Bなんですね!」と反応が返ってくる。いやいや、大事なのは「Aならば」なんですよ。
— 東浩紀 Hiroki Azuma (@hazuma) July 12, 2018
もちろん日常会話はすべて論理的に読まれるわけではないので、意図が伝えられるような工夫は必要となります。
「AならばB」の対偶、真偽の一致はなぜ?
さらに論理学の入門の話をしていきたいと思います。
「AならばB」とセットで覚えておきたいのが、その対偶(contraposition)です。「BでないならばAでない」というのが対偶です。
対偶は、「AならばB」と真偽が一致します。これはAとBがどんな命題だろうが、事実です。
具体例
例えば、\(x\)を実数として、命題Aを「\(x\)が自然数である」、命題Bを「\(x\)が整数である」、としましょう。
このとき、「AならばB」は正しいです。自然数は、整数でもあるからです。
対偶である「BでないならばAでない」は、「\(x\)が整数でないならば、\(x\)は自然数でない」となります。
これもまた正しいですね。\(x\)が整数でないならば、\(x\)が自然数ではありえません。背理法として、もし仮に\(x\)が自然数であったと仮定すると、\(x\)が整数となってしまい、前提と矛盾します。
ちなみに、「BならばA」は「AならばB」の逆(converse)と言います。逆の真偽は一致するとは限りません。
さきほどの例ならば、\(x=-3\)を考えれば、\(x\)は整数ではありますが、自然数ではありません。つまり、「AならばB」は真だが「BならばA」は偽です。
「AならばB」が真であり、かつ「BならばA」が真であるケースもあります。つまり、「AならばB」とその逆の真偽は無関係なのです。
一方で、「AならばB」とその対偶の真偽はいつでも一致します。だから、「AならばB」であることを示すのが難しいときは、その対偶の真偽をチェックしても良いんですね。数学の証明でよく使われるテクニックです。
対偶と真偽が一致すること、真偽表
さて、「AならばB」が正しいとき、なぜ対偶はいつでも正しいのでしょうか。
これは真理値(真、偽のどちらか)を表にして書き下すこと、真偽表を作ることでわかります。要は4パターンの総当たりです。
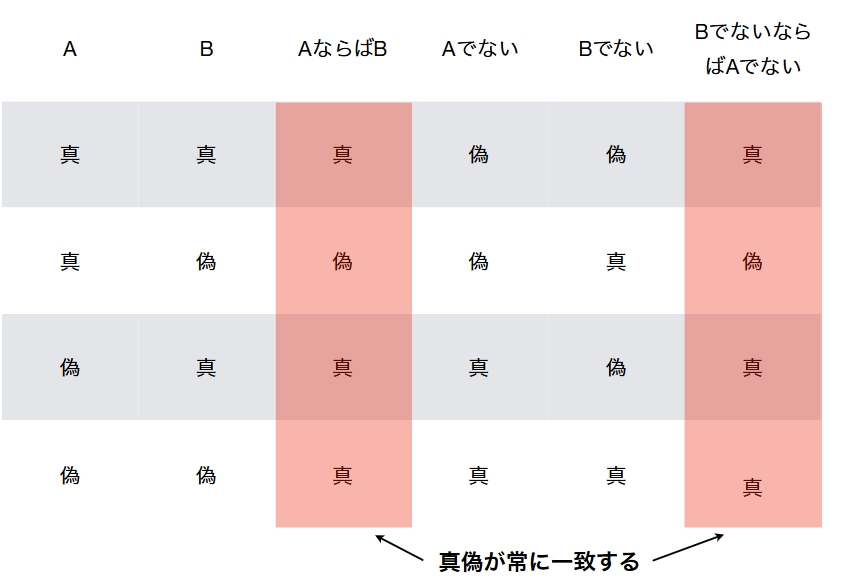
AとBの真偽が、どのような組み合わせだとしても、「AならばB」と「BでないならばAでない」が打ち出す真偽は一致しています。これが対偶と真偽が一致することの証明です。
前提条件を満たさない場合の考え方
「AならばB」において、Aが偽のときに、Bの真偽いかんによらず「AならばB」が真とされることを、疑問に思う人もいるかもしれません。
さきほどの具体例で言えば、\(x\)が自然数でない場合には、そもそも\(x\)が整数であるかどうかは関係がないですよね。「\(x\)が自然数ではないが、\(x\)は整数だった。つまり、AならばBは間違いだ!」というのはめちゃくちゃです。
前提条件を満たさない場合には結論の真偽は問われない。Aでないケースを考えたからといって、「AならばB」は偽りとは言えない。なので、Aが偽のときは常に「AならばB」を真として考える、という意味です。
(前提が偽、すなわち条件が空であるときに正しいと考えることを、空真 vacuous truthと言います。参考:Vacuous truth – Wikipedia)
「AならばB」の否定
「AならばB」を単に「Bである」と受け取ってしまうことはよくある間違いです。
同様によくある間違いが、「AならばB」の否定です。これを「AでないならばB」、あるいは「AならばBでない」と考えてしまうのは正しくアリません。
「AならばB」の否定は、「AではあるがBではない」、つまり「AかつBでない」です。前提条件を満たしているが結論を満たしていないということが、「AならばB」の否定です。
これもさきほどのように真偽表を書けば、否定となっている(つまり、真偽が常に逆転している関係にある)ことがわかります。
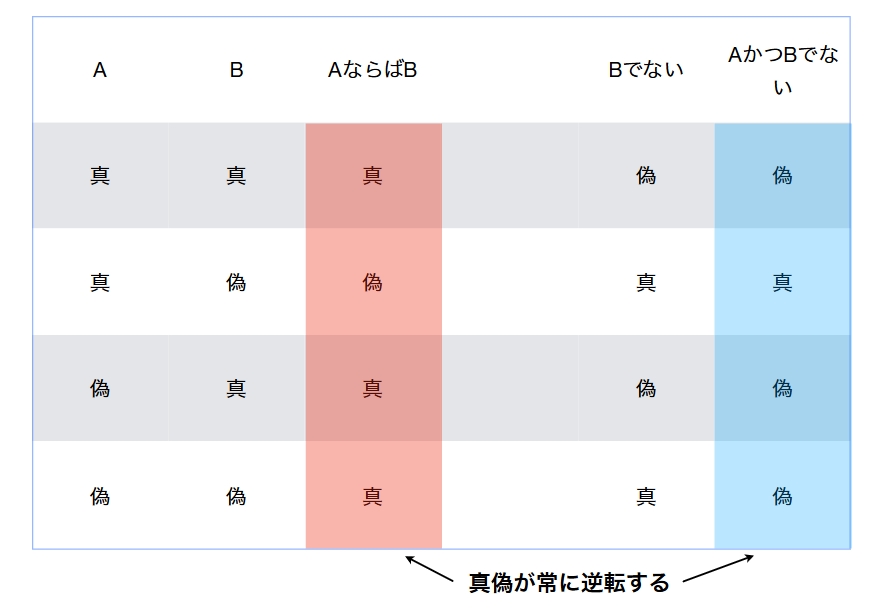
「AならばB」を前提Aが満たされない時に真とする理由は、次のように考えることもできます。
「AならばB」の否定とは何かを論理的に考えると、(AかつBでない)です。この「AかつBでない」を基準とし、それに整合的であるように、「AならばB」の真偽値を決めれば、必然的に上図のような定め方となります。
数学では、値を一義に定めにくいケースが発生したら、他の法則と整合的であるように値を定義することが多いです。そうすれば、例外なく法則が成り立ち、議論が進めやすいので。(これを概念の拡張という)
例えば、\(a^0 =1\)や、負のべき乗は、正のべき乗で成り立っていた指数法則に合わせて定義されます。ただし、0の0乗など、文脈に応じて定義の仕方は変わるケースもあります。
大学数学のために論理学を学びはじめて最初に理解したいのが、「AならばB」という考え方です。
これを単に「Bである」と受け止めるのではなく、「Aという条件が成立するならば、Bという結論が導かれる」と受け止める。そして、Aという条件が成立しないときのことは聞いてないことを理解するのが第一歩でしょう。
そして、その対偶や逆、否定の性質を理解し、真偽表を書いて対応関係を理解できれば、だんだんと論理学のベースはととのってきたと言えるでしょう。
今回の話に加えて、全称命題(すべての~)と存在命題(~が存在する)をおさえておけば、大学数学に入っていくための論理学としては十分でしょう。また別の記事で紹介します。
木村すらいむ(@kimu3_slime)でした。ではでは。