射影行列、射影作用素とは：例、定義、性質

どうも、木村（@kimu3_slime）です。

線形代数では、複合的なベクトルから目的に合った成分を取り出すこと、すなわち射影することを考えます。

今回は、射影行列、射影作用素の例、定義、性質を紹介します。

射影行列、射影作用素とは
- 例
- 定義
射影行列の性質
こちらもおすすめ

射影行列、射影作用素とは

例

最も簡単な例として、

\[ \begin{aligned} P_1 =\begin{pmatrix} 1&0 \\0&0 \end{pmatrix}\end{aligned} \]

のような行列は射影行列です。

平面のベクトル\(x =(x_1,x_2) \in \mathbb{R}^2\)を\(P_1\)で写すと、\(P_1(x) =(x_1,0)\)と第2成分が0になって返ってきます。つまり、ベクトル\(x\)が\(x_2 =0\)という直線（\(y\)軸）に射影されているのです。

上の例では、まっすぐとした射影（直交射影）を考えていますが、そうでないような例もあります。

例えば、\(W_1 =\{x \mid x_2 =0\}\)、\(W_2 =\{x \mid -x_1+x_2 =0\}\)という直線を考え、\(W_2\)に沿った\(W_1\)への射影を考えてみましょう。

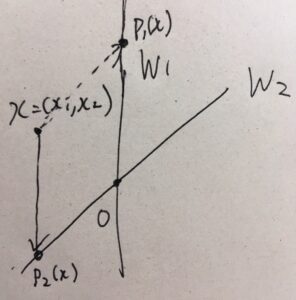
\(x=(x_1,x_2)\)はどのように射影されるでしょうか。直和の問題で考えましたが、\(x= (x_1,x_2)= (0,-x_1+x_2)+(x_1 ,x_1)\)と分解できます。したがって、\(W_1\)射影を表す行列を\(P_2\)とすると、\(P_2 x =(0,-x_1+x_2)\)です。行列の成分を書き下せば、

\[ \begin{aligned}P_2 =\begin{pmatrix} 0&0 \\-1 &1 \end{pmatrix}\end{aligned} \]

とすれば良いですね。

定義

今までの例を抽象化したのが、射影行列です。

正方行列\(P\)が射影行列（projection matrix）であるとは、\(P^2=P\)を満たすこと。特に、対称行列\(P^{\top }=P\)であるときは、直交射影行列（orthogonal projection matrix）と呼ぶ。\(P^2\)とは、2回の積\(PP\)のことです。

さきほどの例が、この定義を満たしていることを確かめてみましょう。

\[ \begin{aligned} P_1^2 &=\begin{pmatrix} 1&0 \\0&0 \end{pmatrix} \begin{pmatrix} 1&0 \\0&0 \end{pmatrix} \\&= \begin{pmatrix} 1&0 \\0&0 \end{pmatrix}\\&= P_1\end{aligned} \]

\[ \begin{aligned} P_2^2 &= \begin{pmatrix} 0&0 \\-1 &1 \end{pmatrix} \begin{pmatrix} 0&0 \\-1 &1 \end{pmatrix}\\ &= \begin{pmatrix} 0&0 \\-1 &1 \end{pmatrix} \\ &= P_2 \end{aligned} \]

なので、これらは射影行列です。

\(P_1\)は対称行列なので、直交射影行列です。一方、\(P_2\)は対称行列でないので、直交射影行列ではありません。

文献によっては、単に射影行列といっただけで、直交射影行列のことを指していることがあります。\(P_2\)のように、直交でない射影は斜行射影と呼ばれるものです。

条件\(P^2 =P\)をべき等性（idempotence）と言いますが、これは一旦影となる空間へ要素を落としたら、影から影へ落としても何も変化がないこと（\(P(Px)=Px\)）を意味しています。

一般に、対角成分がすべて0または1であるような対角行列\(D\)は、直交射影行列です。特に、単位行列やゼロ行列は直交射影行列です。

対角行列の積は、対角成分がそれぞれの対角成分の積であるような対角行列になります。対角成分は\(0^2 =0\)か\(1^2=1\)なので、\(D^2 =D\)を満たします。また、対角行列は対称行列でもあるので、直交射影行列と言えました。

これは三角行列に一般化できません。対角成分がすべて0または1であるような三角行列は、必ずしも射影行列ではありません（後に例を挙げます）。

また、対称行列が必ずしも直交射影行列にならないこともわかりますね。対角成分が0または1でない対角行列は、対称行列ではありますが、直交射影行列ではありません。

行列に限らず、有限次元の線形空間\(V\)上の線形変換\(f: V \to V\)を射影と呼ぶこともできます。

\(f\)が\(f^2 =f\)を満たすとき、射影作用素（projection operator）、射影子と呼びます。

\(V\)が内積空間であるとき、射影作用素が対称性「\(v,w \in V\)に対し\(\langle f(v),w\rangle =\langle v,f(w)\rangle\)」を持つとき、\(f\)を直交射影作用素と呼びます。

射影行列の性質

射影の相補性

射影行列\(P\)があると、単位行列から\(P\)を引いた\(I- P\)も射影行列となります。特に、\(P\)が直交射影ならば、\(I-P\)も直交射影です。これを射影の相補性（complementarity）と言います。

\(I -P\)はなぜ出てくるかというと、一般のベクトル\(x\)は、\(x = Px + (I-P)x\)と分解できるからです。

さて、\(I-P\)が射影行列となることを確かめましょう。\(x \in V\)として、\(P^2=P\)に気をつければ、\((I-P)(I-P)x=(I-P)(x-Px)\\=x-Px-(Px-P^2 x)=x-Px =(I-P)x\)なので、射影行列であることが言えました。

\(P\)が直交射影であるとき、\(I-P\)も直交射影であることを確かめます。転置の性質より、\((I-P)^{\top}= I^{\top}-P^{\top} =I -P\)なので、直交射影と言えました。

また、直交射影\(P\)による像と\(I-P\)による像は直交します。すなわち、\(\langle Px,(I-P)y \rangle =0\)です。

確かめましょう。内積を転置を使って書けば、\(\langle Px,(I-P)y \rangle =(Px)^{\top} (I-P)y\)です。転置の性質と対称性を使えば、\(x^\top P^\top (I-P)y =x^\top P (I-P)y\)で、べき等性を使えば\(x^\top (P-P)y= 0\)です。

そもそも、この変形によって直交射影行列の定義は導かれたと言えるでしょう。\(P\)を一般の行列として、直交条件\(\langle Px,(I-P)y \rangle =0\)が満たされるとします。すると、\(x^\top P^\top (I-P)y=0\)が成り立たなければならない。\(x,y\)は任意なので、\(P^\top -P^\top P=O\)。これは\(P^2 =P,P^\top =P\)と同値です。

直交射影と言いますが、それは\(P\)と\(I-P\)の（像）の直交性を意味しています。したがって、射影行列は直交行列とは限りません。例えば一番最初に紹介した例\(P_1\)は0ベクトルとなる列を含むので、直交行列ではありません。

（また、\(I-P\)を\(P\)の相補行列と呼び、\(P^{\perp}:=I-P\)と書くことがあるようです。）

直和分解

射影行列があると、任意のベクトル\(x\)を射影成分\(Px\)とそれ以外\((I-P)x\)にただ一通りに分解できます。

和空間の言葉で言えば、\(\mathbb{R}^N = P(\mathbb{R}^N) \dot{+} \ker P\)と、射影の像\(P(\mathbb{R}^N)\)と核\(\ker P\)の直和に表せます。

確かめてみましょう。

まず、\(P\)の核は\(I-P\)の像に等しいです \(\ker P = (I-P)(\mathbb{R}^N)\)。\(x \in \ker P\)とは、\(Px =0\)のことです。\(x = Px + (I-P)x\)という分解を考えれば、それは\(x= (I-P)x\)と同値です。すなわち、\(x\)は\(I-P\)の像に属することと同値であることがわかりました。

分解\(x = Px + (I-P)x\)において、\(Px \in P(\mathbb{R}^N)\)、\((I-P)x \in (I-P)(\mathbb{R}^N) = \ker P\)なので、\(\mathbb{R}^N = P(\mathbb{R}^N) +\ker P\)と和空間であることがわかりました。

残りは直和であること、\(P(\mathbb{R}^N) \cap \ker P= \{0\}\)を示します。それぞれは部分空間なので、\(P(\mathbb{R}^N) \cap \ker P \supset \{0\}\)です。一方、\(x\in P(\mathbb{R}^N) \cap \ker P\)を任意のものとします。像の定義より、\(x = Py\)となる\(y\)が存在します。核の要素でもあるので、\(P\)を作用させれば\(0 =Px =P(Py)\)です。\(P\)は射影行列なので\(P(Py)=Py=0\)です。よって、\(x= Py=0\)が導かれ、\(P(\mathbb{R}^N) \cap \ker P= \{0\}\)が言えました。

逆に、\(V= W_1 \dot{+} W_2\)という直和分解が得られているとき、\(v =x+y\)という分解から\(Pv =x\)と写像を定めると、それは射影作用素になります。（直和分解を使って射影を定義することもある。）

参考：部分空間の直和とは：定義と例、射影

また、\(P\)が直交射影行列の場合は、\(\mathbb{R}^N = P(\mathbb{R}^N) \oplus \ker P\)です。つまり、像は核の直交補空間となります \((\ker P)^{\perp} =P(\mathbb{R}^N) \)。すなわち、射影行列においては、像と核が相補的な関係にあるわけです。

\(P\)が直交射影行列のときの\(P\)と\(I-P\)の直交性は、さきほど示した通りです。それによって、像の要素と核の要素はすべて必ず直交します。

逆に、\(V= W_1 \oplus W_1^{\perp}\)という直和分解が得られているとき、\(v =x+y\)という分解から\(Pv =x\)と写像を定めると、それは直交射影作用素になります。

参考：直交補空間、直交直和、直交射影とは：定義と例、証明

可逆性、行列式

射影行列の可逆性について考えてみましょう。

行列式は必ず0または1になります。

\(P^2= P\)と行列式の積の性質を用いれば、\(( \det P)^2=\det P^2 = \det P \)です。これを\(\det P \)について解けば、\(\det P = 0,1\)ですね。

実際は、射影行列と呼ぶときは行列式が0のケース、押しつぶしているときを考えることが多いでしょう。

行列式が1であるような射影行列は、単位行列になることが示せます。

\(P\)の行列式が0でないので、逆行列\(P^{-1}\)が存在します。\(P^2 =P\)の両辺に\(P^{-1}\)をかければ、\(P =P^{-1}P^2 =P^{-1}P =I\)が得られました。

固有値

射影行列の固有値は、0または1に限られます。

\(x \neq 0\)として、\(Px =\lambda x\)と仮定しましょう。両辺に\(P\)を作用させ、\(P^2=P\)を使えば、\(Px =P^2 x = P(\lambda x) = \lambda ^2 x\)です。よって、\(\lambda x = \lambda ^2 x\)ですが、\(x \neq 0 \)より\(\lambda ^2 =\lambda \)となります。これを解けば、\(\lambda\)は0または1とわかりました。

逆は一般には成り立ちません。固有値が0または1であるからといって、射影行列とは言えません。例えば

\[ \begin{aligned} &\begin{pmatrix} 1&1\\0&1 \end{pmatrix} \begin{pmatrix} 1&1\\0&1 \end{pmatrix} = \begin{pmatrix} 1&2\\0&1 \end{pmatrix}\end{aligned} \]

は、固有値がすべて1ですが、べき等性\(P^2=P\)を満たしません。

半正定値性

直交射影行列は、半正定値行列となります \( P \geq 0\)。すなわち、すべての\(x\)に対し、\(\langle x, Px\rangle \geq 0\)を満たします。

確かめてみましょう。

\[ \begin{aligned} \langle x, Px\rangle &= \langle x, P^2x\rangle \\ &= x^{\top} P^2 x \\&= x^{\top}P^\top Px \\&= (Px)^{\top} Px \\ &= \langle Px,Px \rangle \geq 0\end{aligned} \]

最後は内積の正定値性を用いています。

直交射影は最良近似

直交射影行列については、\(\|Px\| \leq \|x\|\)が必ず成り立ちます。

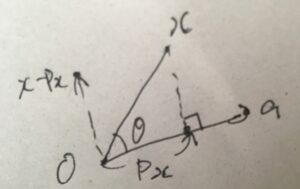
図的・幾何学的には当然のことですが、きちんと証明しましょう。

\(x= Px +(I-P)x\)という分解において、\(Px, (I-P)x\)が直交していることに注意します。ノルムと内積の関係、内積の線形性を使って整理すれば、

\[ \begin{aligned} \|x\|^2 &= \| Px +(I-P)x \|^2 \\&= \langle Px +(I-P)x,Px +(I-P)x \rangle \\&= \langle Px +(I-P)x,Px\rangle + \langle Px +(I-P)x,(I-P)x\rangle \\&= \langle Px,Px\rangle + \langle (I-P)x,(I-P)x\rangle \\& \geq \langle Px,Px\rangle \\&= \|Px\|^2 \end{aligned} \]

となるので、平方根を取れば\(\|Px\| \leq \|x\|\)が得られました。

短くまとめれば、直交条件よりピタゴラスの定理\(\|x\|^2 = \|Px\|^2+\|(I-P)x\|^2\)が成り立つので、一方のノルムを落として下から評価しているということです。

直交射影行列でなければ、この関係は必ずしも成り立ちません。

\[ \begin{aligned}P_2 =\begin{pmatrix} 0&0 \\-1 &1 \end{pmatrix}\end{aligned} \]

とすると、\(P_2 x =(0,-x_1+x_2)\)です。\(x=(-1,1)\)のときを考えると、\(\|P_2 x\|=\sqrt{(-x_1+x_2)^2} =2\)、\(\|x\|= \sqrt {2}\)なので、\(\|P_2 x\|> \|x\|\)となっています。

実際、直交射影\(Px\)は像\(P(\mathbb{R}^N)\)への射影のうち、最も\(x\)をよく近似しているベクトル（最良近似）と言えます。

すなわち、\(y \in P(\mathbb{R}^N)\)かつ\(y \neq Px\)ならば、\(\|x-Px\| < \|x-y\|\)です（\(x\)との誤差が最も小さいのが\(Px\)である）。

\(x-y =(x-Px)+(Px-y)\)と分解すると、\(x-Px \in \ker P\)、\(Px-y \in P(\mathbb{R}^N)\)です。\(P\)は直交射影なので、これらのベクトルは直交しています。したがって、さきほどと同様の計算により、\(\|x-y\|^2=\|x-Px\|^2 +\|Px-y\|^2\)となります。ここで、\(Px \neq y\)なので\(\|Px-y\|^2 >0\)であり、\(\|x-y\|^2>\|x-Px\|^2\)が得られました。

以上、射影行列、射影作用素とは何か、その例、定義、性質を紹介してきました。

射影行列は、最小二乗法や、行列の対角化、スペクトル分解に表れるものです。\(P^2=P\)という定義と射影のイメージ、直和分解、\(I-P\)との相補性といった概念をスムーズに行き来できるようになってみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。