どうも、木村(@kimu3_slime)です。
今回は、部分空間の直和とは何か、定義と例、射影について紹介します。
部分空間の直和
例
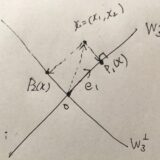
線形空間として、\(V = \mathbb{R^2}\)という平面を考えましょう。
これに対して、\(W_1 =\{x \mid x_1 =0\}\)、\(W_2 = \{x \mid -x_1 +x_2 =0\}\)と置くと、これらは1次元の部分空間(直線)です。
部分空間に対しては、その和空間を考えることができました。この例では、\(x= (x_1,x_2)= (0,-x_1+x_2)+(x_1 ,x_1)\)と分解できるので、\(W_1 +W_2 = \mathbb{R}^2\)となります。
これは重複のない和、直和の例です。共通部分を考えると、\(W_1 \cap W_2 =\{0\}\)となっています。
微妙な例ですが、\(W_ 3 = \mathbb{R}^2\)とすると、\(\mathbb{R}^2= W_1 +W_3\)という和空間として表せます。
確かにこれは和空間ではありますが、重複があります。すなわち、\(W_1 \cap W_3 = W_1 \neq \{0\} \)です。そして、\(\mathbb{R}^2\)の成分をただ一通りに分解することができません。\((x_1,x_2)= (0,x_2)+(x_1,0)=(0,\frac{1}{2}x_2)+(x_1,\frac{1}{2}x_2)\)といったように、2通りに表せてしまいます。
定義
以上のことを一般化して、\(V =W_1 + W_2\)かつ\(W_1 \cap W_2 =\{0\}\)であるとき、和空間\(W_1+ W_2\)は直和(direct sum)であると呼ばれます。そして、\(W_1 \dot {+}W_2\)とドットをつけて書きます。
また、\(V\)を中心に見たとき、\(V = W_1 \dot {+}W_2\)と表せるとき、それを\(V\)の直和分解(direct sum decomposition)と呼びます。
文献によっては直和を\(W_1 \oplus W_2\)と書きます。ここでは、その記号は特殊な直和、直交直和を表すのに使いたいです。記号の意味は文脈次第なので注意しましょう。
また、\(W_1 \dot {+}W_2\)と書いてあったら、それは「\(V =W_1 + W_2\)かつ\(W_1 \cap W_2 =\{0\}\)である」ことを意味します。直和\(\dot{+}\)という新たな演算が定義されたわけではなく、集合としては単に和空間であることに注意しましょう。特殊な和空間であるときに、使う記号を変えて簡略表記しているだけです。
直和の定義には、同値な言い換えがあります。
- \(W_1 \cap W_2 =\{0\}\)
- \(V\)の任意の要素が、\(W_1,W_2\)の要素の和としてただ一通りに表される
1から2を示しましょう。\(v \in V\)を任意の要素として、\(v =x+y=p+q\)と2通りに表されたとします。\(x,p \in W_1\)、\(p,q \in W_2\)です。移項すると\(x-p =q-y\)です。左辺は\(W_1\)の要素、右辺は\(W_2\)の要素なので、両辺は\(W_1 \cap W_2\)の要素です。仮定\(W_1 \cap W_2 =\{0\}\)より、\(x-p=q-y=0\)、すなわち\(x=p,q=y\)です。表し方が1通りであると言えました。
2から1を示します。\(W_1, W_2\)は線形空間なので、原点を含み、\(W_1 \cap W_2 \supset \{0\}\)であることは良いでしょう。\( v \in W_1 \cap W_2\)とします。これは見方によって、2通りに分解できるのです。\(v= v+0\)、\(v\in W_1,0 \in W_2\)、\(v= 0+v\)、\(0\in W_1,v \in W_2\)というように。仮定より表し方は一通りなので、\(v=0\)でなければなりません。よって、\(W_1 \cap W_2 =\{0\}\)が言えました。
次元
一般に部分空間の和空間の次元については
\[ \begin{aligned}\dim(W_1+W_2)=\dim W_1 +\dim W_2 -\dim (W_1 \cap W_2)\end{aligned} \]
が成り立ちました。直和では、共通部分の次元が0なので、
\[ \begin{aligned}\dim(W_1\dot{+}W_2)=\dim W_1 +\dim W_2 \end{aligned} \]
という単純な等式が得られます。
もし\(\dim(W_1+W_2) \neq \dim W_1 +\dim W_2 \)ならば、即座にそれは直和でないと結論できるわけですね。
複数の直和
2つの部分空間の直和を考えてきましたが、3つ以上の直和を考えることもできます。
\(W_1,W_2,W_3\)を部分空間として、その和空間を
\[ \begin{aligned}W_1 + W_2 +W_3 :=\{w_1+w_2+w_3 \mid \\ w_1 \in W_1,w_2 \in W_2,w_3 \in W_3\}\end{aligned} \]
と定義します。それが直和であるとは、\(W_1 \cap(W_2+W_3)=\{0\}\)、 \(W_2 \cap(W_1+W_3)=\{0\}\)、\(W_3 \cap(W_1+W_2)=\{0\}\)であることです。\(v= w_1+w_2+w_3\)と\(W_1,W_2,W_3\)の要素としてただ一通りに表せるとも言い換えられます。
\(W_1 \dot{+} W_2\)、\(W_2 \dot{+} W_3\)という2つの直和があるからといって、3つが直和\(W_1 \dot{+}W_2 \dot{+} W_3\)とは言えないことに注意しましょう。
例えば、\(W_1 =\{x \mid x_1 =0\}\)、\(W_2 = \{x \mid -x_1 +x_2 =0\}\)、\(W_3 = \{x \mid x_1 +x_2 =0\}\)と置くと、2つの和は直和\(W_1 \dot{+} W_2\)、\(W_2 \dot{+} W_3\)です。しかし、\(W_1 +W_2 =\mathbb{R}^2\)なので、\(W_3 \cap (W_1 +W_2) = W_3 \neq \{0\}\)で、3つの和は直和ではありません。複数の和が直和になるか考えるときに、2つだけ取り出してもダメなのです。
部分空間への射影
\(V= W_1\dot {+} W_2\)という直和があると、\(V\)の要素を「成分分解」することができます。
\(v \in V\)とすると、\(v =x+y\)、\(x\in W_1, y \in W_2\)と一通りに表せます。そこで、
\[ \begin{aligned}P_1 (v) := x\end{aligned} \]
\[ \begin{aligned}P_2 (v) := y\end{aligned} \]
と写像\(P_1,P_2 :V \to V\)を定めましょう。これを部分空間\(W_1,W_2\)への射影(projection)と呼びます。
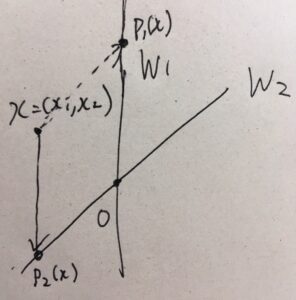
例えば、\(W_1 =\{x \mid x_1 =0\}\)、\(W_2 = \{x \mid -x_1 +x_2 =0\}\)ならば、\(x= (x_1,x_2)= (0,-x_1+x_2)+(x_1 ,x_1)\)と分解できるので、
\[ \begin{aligned}P_1 (x) = (0,-x_1+x_2)\end{aligned} \]
\[ \begin{aligned}P_2 (x) = (x_1 ,x_1)\end{aligned} \]
となっています。部分空間を新たな軸として、その軸に向けて影を落としていますね。
一般に、射影\(P_1\)は、線形写像であり、\(P_1^2 =P_1\)を満たします。
\(v= x+y\)、\(w =p+q\)と分解すると、\(P_1 (v+w)=P_1((x+p)+(y+q))\\=x+p=P_1(v)+P_1(w)\)です。また、\(P_1(av) =P_1(ax+ay)=ax =aP_1 (w)\)なので、線形写像です。
\(v \in V\)を任意の要素とすると、\( P_1 (v) =x\)です。したがって、さらに作用させても\(P_1 (P_1 (v))= P_1 (x) =x\)です。\(P_1^2 =P_1\)が言えました。
射影\(P_2\)についても、全く同様の性質が示せます。一般に、これらを射影作用素(projection operator)と呼びます。ベクトルの射影については、別記事でも紹介予定。
直和分解と対角化
直和による分解をどうして考えるか。そのモチベーションのひとつは、行列の対角化にありるのではないでしょうか。
行列には必ず固有値と固有ベクトルがありますが、固有ベクトルが生成する空間を固有空間と呼びます。\(n\)次の正方行列が対角化できることの必要十分条件は、
\[ \begin{aligned}\mathbb{R}^n = W_1 \dot {+}W_2 \dot {+} \cdots \dot {+}W_k\end{aligned} \]
と全体が固有空間の直和に表されることです。
\(A = \lambda_1 P_1 +\lambda_2 P_2\)のような行列のスペクトル分解は、固有空間への直和分解を利用したものと言えます。
参考:対称行列の性質:内積による特徴づけ、逆行列、固有値、対角化について
また、ジョルダン標準形の理論では、行列を上三角なブロック行列に変形します。固有空間が直和分解とならないときに、工夫して空間の直和分解を得ていると言えます(広義固有空間を考える)。
少し難しくなりましたが、簡単に言えば、\(V =W_1 +W_2\)と適切に空間を直和分解することが、行列を対角行列など簡単な形に変形することに対応しているわけですね。
以上、部分空間の直和とは何か、その定義や例、射影、対角化との関係を紹介してきました。
直和からつながる話として、直交直和や直交補空間といった内積を交えた話があります。これは別記事にて。
この記事を通して、部分空間の直和が、空間を独立にバラバラにできるというイメージをつかんでもらえれば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
共立出版 (1982-07-09T00:00:01Z)
¥788 (中古品)
世界標準MIT教科書 ストラング:線形代数イントロダクション
近代科学社 (2015-12-22T00:00:01Z)
¥14,721 (コレクター商品)
東京大学出版会 (2019-03-08T00:00:00.000Z)
¥1,870
こちらもおすすめ
行列の対角化可能性の定義とメリット、例、同値条件について解説
対称行列の性質:内積による特徴づけ、逆行列、固有値、対角化について