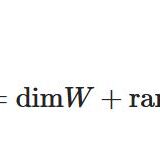部分空間の基底、次元の求め方（生成、共通部分、和空間）

どうも、木村（@kimu3_slime）です。

今回は、生成する部分空間、共通部分、和空間といった部分空間の次元、基底の求め方を紹介します。

前提知識：部分空間とは：例、判定法、証明の書き方、部分空間の共通部分、和空間とは：例と証明

生成する部分空間の基底、次元
共通部分の基底、次元
和空間の基底、次元
こちらもおすすめ

生成する部分空間の基底、次元

いくつかのベクトルが生成する部分空間の基底、次元を求めてみましょう。

\[ \begin{aligned}a_1,a_2,a_3 =\begin{pmatrix} 1\\ 2 \\1\end{pmatrix},\begin{pmatrix} 2\\ 1 \\2\end{pmatrix}, \begin{pmatrix} 0\\ -3 \\0\end{pmatrix}\end{aligned} \]

として、\(a_1,a_2,a_3\)が生成する部分空間を\(W_1\)としましょう。\(W_1 := \mathrm {span}(\{a_1,a_2,a_3\})\)です。

一般に、\(S=\{v_1,\dots,v_k\}\subset \mathbb{R}^N\)が生成する空間とは、

\[ \begin{aligned}\mathrm{span}(S):=\{v \in \mathbb{R}^N \mid c_1,\dots,c_k \\ なる係数が存在して \; v = c_1 v_1+ \cdots + c_k v_k と表せる\}\end{aligned} \]

のことでした。線形結合で表せるベクトルをすべて集めてできる部分空間です。

参考：実数空間、線形結合、線形部分空間、次元とは何か：2次元を例に

\(W_1\)の基底と次元を求めます。基底とは、線形独立でその空間を生成しているベクトルの組のことでした。

いくつかのベクトルから線形独立なものを見つけ出すには、行列の基本変形が有効です。

\[ \begin{aligned} &\begin{pmatrix} 1&2&0 \\ 2&1&-3 \\ 1&2&0 \end{pmatrix} \\& \sim\begin{pmatrix} 1&2&0 \\ 0&-3&-3 \\ 0&0&0 \end{pmatrix} \end{aligned} \]

この行列のランクは2なので、2本のベクトルだけが線形独立です。

\(a_1,a_2\)が\(W_1\)の基底であることを示しましょう。基本変形によって、\(a_1,a_2\)が線形独立であることは示しました。\(W_1\)のすべての要素は、\(a_1,a_2\)の線形結合として示せるでしょうか。基本変形の結果によって、\(-2a _1 +a_2=a_3\)がわかります。\(w \in W_1\)を任意に選ぶと、\(w = c_1a_1+c_2 a_2+c_3a_3\)と表せるわけです。これを整理すれば、\(w=(c_1 -2c_3)a_1+(c_2+c_3)a_2\)と表せます。よって、\(a_1,a_2\)が\(W_1\)を生成していることを示せました。

次元とは、基底の個数のことです。\(\mathrm{dim} W_1 =2\)が示せました。

もうひとつやってみましょう。

\(W_2\)を、

\[ \begin{aligned}b_1,b_2,b_3 =\begin{pmatrix} 3\\ 2 \\-1\end{pmatrix},\begin{pmatrix} 0\\ 1 \\2\end{pmatrix}, \begin{pmatrix} 6\\ 5 \\0\end{pmatrix}\end{aligned} \]

が生成する部分空間としましょう。

行列としてベクトルを並べ、基本変形します。

\[ \begin{aligned} &\begin{pmatrix} 3&0&6 \\ 2&1&5 \\ -1&2&0 \end{pmatrix} \\& \sim\begin{pmatrix} 1&0&2 \\ 2&1&5 \\ -1&2&0 \end{pmatrix}\\& \sim\begin{pmatrix} 1&0&2 \\ 0&1&1 \\ 0&2&2 \end{pmatrix} \\& \sim\begin{pmatrix} 1&0&2 \\ 0&1&1 \\ 0&0&0 \end{pmatrix} \end{aligned} \]

となるので、ランクは2です。

したがって、\(b_1,b_2\)は線形独立です。\(b_3 =2b_1+b_2\)なので、\(b_1,b_2\)が\(W_2\)を生成しています。よって、\(b_1,b_2\)が基底であり、\(\mathrm{dim }W_2 =2\)とわかりました。

共通部分の基底、次元

\(W_1,W_2\)の共通部分\(W_1 \cap W_2\)の次元を求めてみましょう。（共通部分は部分空間となる）

そのためには、\(a_1,a_2,a_3,b_1,b_2,b_3\)がどんな関係があるかを知っておく必要があります。さきほどの結果から\(a_1,a_2,b_1,b_2\)のみ調べれば良いです。しかし、次に和空間の基底も求めたいので、セットで扱います。

行列\(A= (a_1,a_2,a_3,b_1,b_2,b_3)\)の基本変形を考えます。

\[ \begin{aligned} &\begin{pmatrix} 1&2&0 &3&0&6\\ 2&1&-3 &2&1&5 \\ 1&2&0 &-1&2&0\end{pmatrix} \\& \sim\begin{pmatrix} 1&2&0 &3&0&6\\ 0&-3&-3 &-4&1 &-7 \\ 0&0&0&-4&2&-6 \end{pmatrix} \end{aligned} \]

\(b_1,b_2\)に対応する列で第3成分が0になるように考えると、\(b_1+2b_2=\frac{2}{3}a_1+ \frac{2}{3}a_2\)が成り立ちます。

そこで、\(c:= b_1+2b_2\)と置きましょう。それは\(a_1,a_2\)の線形結合であり、\(b_1,b_2\)の線形結合でもあるので、\(c \in W_1 \cap W_2\)です。

\(c\)が\(W_1 \cap W_2\)の基底であることを示します。0でないベクトル1つなので、線形独立です。

生成していることを確かめましょう。\(w \in W_1 \cap W_2\)を任意に選ぶと、\(w= c_1 a_1+c_2a_2 =d_1 b_1 +d_2 b_2\)と表せます。基本変形の結果から、成分を比較すると、\(c_1+2c_2 =3d_1\)、\(-3c_2 =-4d_1+d_2\)、\(0=-4d_1+2d_2\)が成り立ちます。後ろから整理すると、\(d_2 =2d_1\)です。したがって、\(w= d_1b_1+2d_1b_2 =d_1(b_1+2b_2)=d_1 c\)と表せました。

よって、\(c\)は\(W_1\cap W_2\)の基底で、\(\mathrm{dim}(W_1 \cap W_2)=1\)です。

基底を見つける手順が、少しわかりにくかったでしょうか。\(W_1 \cap W_2\)の要素は、一般に\(w= c_1 a_1+c_2a_2 =d_1 b_1 +d_2 b_2\)と表されます。この中から、本質的に必要なものを見つけたいわけです。そこで基本変形の結果を見ると、係数\(c_1,c_2,d_1,d_2\)に制限がかかって（例えば\(d_2 =2d_1\)のように）、特定の形をしなければならないことがわかります。それが\(c=b_1+2b_2\)のスカラー倍でなければならない、ということです。

和空間の基底、次元

最後に、和空間\(W_1 + W_2\)の基底と次元を求めてみましょう。部分空間の和空間とは、単なる和集合ではなく、

\[ \begin{aligned}W_1 + W_2 := \{z \mid x \in W_1 ,y \in W_2 によって z= x+y と表せる\}\end{aligned} \]

でした。つまり、\(W_1,W_2\)のベクトルによって生成される部分空間です。

参考：部分空間の共通部分、和空間とは：例と証明

今回の問題ならば、\(W_1,W_2\)の定義から、\(W_1+W_2\)とは\(a_1,a_2,a_3,b_1,b_2,b_3\)によって生成される部分空間のことです。

そのうち線形独立なものがいくつあるかと言えば、行列の基本変形で発見できます。

\[ \begin{aligned} &\begin{pmatrix} 1&2&0 &3&0&6\\ 2&1&-3 &2&1&5 \\ 1&2&0 &-1&2&0\end{pmatrix} \\& \sim\begin{pmatrix} 1&2&0 &3&0&6\\ 0&-3&-3 &-4&1 &-7 \\ 0&0&0&-4&2&-6 \end{pmatrix} \end{aligned} \]

よってこの行列のランクは3です。

例えば、\(a_1,a_2,b_1\)は線形独立です。\(\mathbb{R}^3\)の次元は3で、4本以上のベクトルが線形独立になることはありません。したがって、\(a_3,b_2,b_3\)は\(a_1,a_2,b_1\)の線形結合として表せます。

よって、\(a_1,a_2,b_1\)は\(W_1 +W_2\)の基底であり、\(\mathrm{dim}(W_1+W_2) =3\)がわかりました。特に、\(W_1+ W_2 =\mathbb{R}^3\)となるわけです。

今回の結果をまとめると、

\[ \begin{aligned}\mathrm{dim}W_1 = 2, \mathrm{dim}W_2 =2\end{aligned} \]

\[ \begin{aligned}\mathrm{dim}(W_1 \cap W_2)=1, \mathrm{dim}(W_1+W_2) =3\end{aligned} \]

です。次のような等式が成り立ちますね。

\[ \begin{aligned}\mathrm{dim}(W_1+W_2) = \mathrm{dim}W_1+\mathrm{dim}W_2-\mathrm{dim}(W_1 \cap W_2)\end{aligned} \]

これは今回の例に限らず、一般の部分空間\(W_1,W_2\)とその共通部分、和空間について成り立つ等式です。例えば「線型代数入門」4章を参照。

以上、部分空間の基底、次元の求め方を紹介してきました。