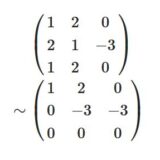線形独立・従属の判定法：行列のランクとの関係

どうも、木村（@kimu3_slime）です。

「与えられたベクトルの組は線形独立かどうか判定せよ」といった問題は、部分空間の基底や次元を求める上で重要です。

今回は、線形独立・従属の判定法として、行列のランクとの関係を紹介したいと思います。

線形独立性とランクの関係
具体例
こちらもおすすめ

線形独立性とランクの関係

\(a_1,a_2,\dots,a_m\)というベクトルの組が線形独立かどうか判定したいとしましょう。

\(a_1,a_2,\dots,a_m \in \mathbb{R} ^n\)、行列を\(A:=(a_1,\dots, a_m)\)とします。

行列\(A\)のランク\(\mathrm{rank}A\)は、\(A\)の線形独立な列ベクトルの最大数に等しい。（行についても同様）

おおざっぱな理屈はこうです。まず、行列の基本変形によって、ベクトルの線形独立性は変化しません。そのため、行列のランクは、その像の次元に等しい。それが線形独立なベクトルの最大数です。詳しくは、齋藤「線型代数入門」4章を参照。

具体例

次のベクトルの組は線形独立でしょうか？

\[ \begin{aligned} a_1,a_2,a_3 =\begin{pmatrix} 1\\ 2 \\1\end{pmatrix},\begin{pmatrix} 2\\ 1 \\2\end{pmatrix}, \begin{pmatrix} 2\\ 1 \\1\end{pmatrix}\end{aligned} \]

それを判定するために、ベクトルを並べた行列を作り、基本変形しましょう。

\[ \begin{aligned} &\begin{pmatrix} 1&2&2 \\ 2&1&1 \\ 1&2&1 \end{pmatrix} \\& \sim\begin{pmatrix} 1&2&2 \\ 0&-3&-3 \\ 0&0&-1 \end{pmatrix} \end{aligned} \]

となるので、ランクは3で、線形独立であることがわかりました。

もうひとつやってみましょう。

\[ \begin{aligned} b_1,b_2,b_3,b_4 =\begin{pmatrix} 2\\ 0 \\-3 \\-4\end{pmatrix},\begin{pmatrix} 0\\ 3 \\1 \\ 2\end{pmatrix}, \begin{pmatrix} 1\\ 2 \\1 \\ 0 \end{pmatrix} , \begin{pmatrix} 0\\ -1 \\-4 \\ -2 \end{pmatrix}\end{aligned} \]

\[ \begin{aligned} &\begin{pmatrix} 2&0&1&0 \\ 0&3&2 & -1 \\ -3&1&1&-4 \\ -4 &2& 0 &-2\end{pmatrix} \\& \sim\begin{pmatrix} 2&0&1&0 \\ 0&3&2 & -1 \\ 0&1&\frac{5}{2}&-4\\ 0 &2& 2 &-2\end{pmatrix} \\& \sim\begin{pmatrix} 2&0&1&0 \\ 0&1&\frac{2}{3} & -\frac{1}{3} \\ 0&1&\frac{5}{2}&- 4\\ 0 &1& 1 &-1\end{pmatrix}\\& \sim\begin{pmatrix} 2&0&1&0 \\ 0&1&\frac{2}{3} & -\frac{1}{3}\\ 0&0&\frac{11}{6}&- \frac{11}{3} \\ 0 &0& \frac{1}{3} &-\frac{2}{3}\end{pmatrix} \\& \sim\begin{pmatrix} 2&0&1&0 \\ 0&-\frac{1}{3}&\frac{2}{3} & 1 \\ 0&0&1&- 2\\ 0 &0& 0 &0\end{pmatrix}\end{aligned} \]

と基本変形できるので、ランクは3で、線形独立ではありません（線形従属）。

さらに基本変形すると、\(b_4\)を他の3つのベクトルで表せます。

\[ \begin{aligned} & \begin{pmatrix} 2&0&1&0 \\ 0&-\frac{1}{3}&\frac{2}{3} & 1 \\ 0&0&1&-2 \\ 0 &0& 0 &0\end{pmatrix} \\ & \sim \begin{pmatrix} 1&0&\frac{1}{2}&0 \\ 0&1&-2 & -3 \\ 0&0&1&-2 \\ 0 &0& 0 &0\end{pmatrix} \\ & \sim \begin{pmatrix} 1&0&0&1 \\ 0&1&0 & 1 \\ 0&0&1&- 2\\ 0 &0& 0 &0\end{pmatrix}\end{aligned} \]

\(b_4 = 1b_1 +1 b_2 -2 b_3\)です（確かめてみてください）。

以上、ベクトルの組が線形独立かどうか判定する方法として、行列のランクとの関係を紹介してきました。

ベクトルの組が生成する部分空間の基底を探したり、次元を求めたりするときもこの方法は使えます。

パッと見で線形独立性を判定できるような問題ならば、この方法を使わなくても良いです。しかし、ちょっと複雑な問題ならば、行列として基本変形して判定した方が楽でしょう。標準形にすると、ベクトル同士の依存関係がわかりやすいです。

木村すらいむ（@kimu3_slime）でした。ではでは。