線形方程式と線形写像の像、次元とランクの関係

どうも、木村（@kimu3_slime）です。

今回は、線形方程式が解けることと線形写像の像の関係、像の次元とランクの関係、ついて解説します。

線形方程式が解けることと、線形写像の像の関係
像の次元とランクの関係
こちらもおすすめ

線形方程式が解けることと、線形写像の像の関係

線形方程式には、解けるものもあれば、解が存在しないものもあります。それらを区別するには、どうしたら良いのでしょうか？

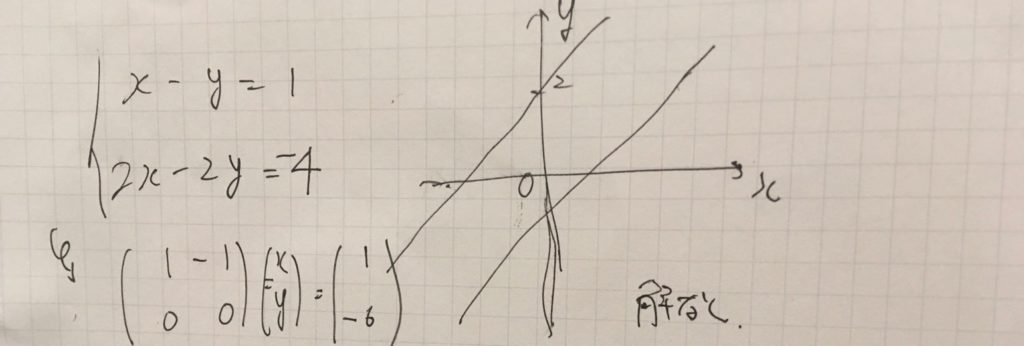
解のない例が、次のものです。

\( \begin{pmatrix} 1& -1\\ 2 & -2 \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix} = \begin{pmatrix} 1\\ -4 \end{pmatrix}\)

参考：1次方程式を行列で解くメリット・方法・条件について、幾何学的に見る

この式を線形写像として捉え直してみましょう。両辺を一般に\(Ax=b\)と置きます。

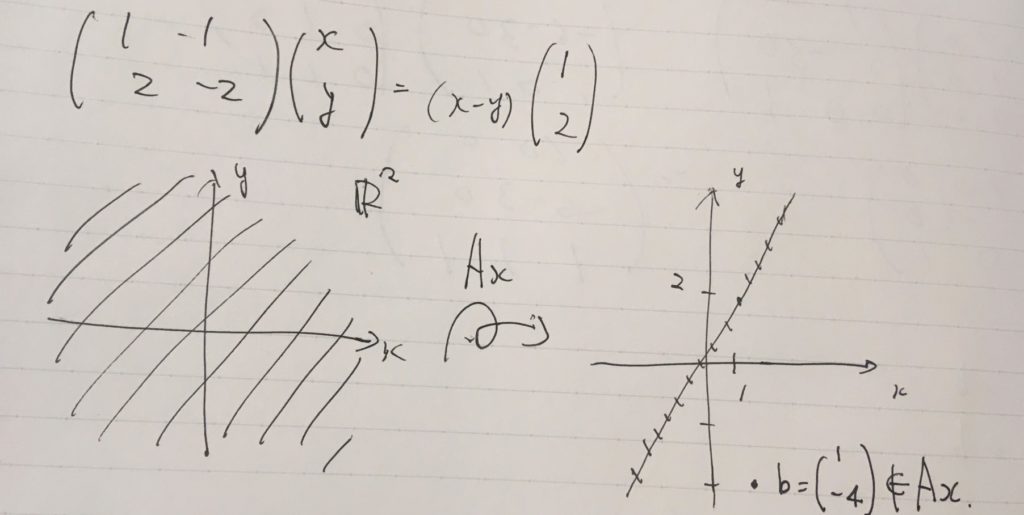
まず左辺だけに注目します。線形写像\(A\)を線形写像として見るということは、不特定多数の\(x\)に対して、\(Ax\)を対応させる規則として見ることです。

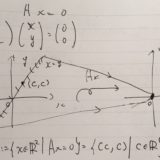
平面\(\mathbb{R}^2\)を写す先の全体（\(A\)の像）が、今回はある直線に限定されていることが見て取れますね。全体としては、2次元の広がりのある空間が、1次元の直線へと潰されたわけです。例えば、左側における\(x=y\)の直線で表される点\((x,y)\)は、すべて\(Ax=(0,0)\)と1点へと写されています。

どんな風に\((x,y)\)を選んだとしても、結局は\((1,2)\)ベクトルの直線上へ写ってしまう。もともとの問題の右辺\(b=(1,-4)\)には決して写らない。だから、解は存在しないというわけです。

\(A\)を行列（＝線形写像）とします。\(A\)によって写される点\(Ax\)を集めた集合を、\(A\)の像 \(A(\mathbb{R}^N )\)と言います。

\(A(\mathbb{R}^N ):= \{ b \in \mathbb{R}^N \mid \exists x ( Ax =b ) \}\)

線形写像の像は、必ず線形部分空間となり、次元が定まっています。

すると、線形方程式\(Ax =b\)が解けることは、\(b\)が\(A\)の像に属すること

\(\exists x (Ax =b ) \Leftrightarrow b \in A(\mathbb{R}^N )\)

と言い換えられます。

もし\(A\)の像が大きければ解が得られるケースは多くなり、像が小さければ解が得られるケースは少なくなります。大きい、小さいとは、像の（部分空間としての）次元のことです。

極端な話、ゼロ行列\(A=O\)の場合、\(A(\mathbb{R}^N)=\{0\}\)で、像の次元は0です（基底が存在しないとき、次元は0と約束している）。つまり、\(b=0\)のケースしか解は存在しません。

参考：実数空間、線形結合、線形部分空間、次元とは何か：2次元を例に

線形写像\( \begin{pmatrix} 1& -1\\ 2 & -2 \end{pmatrix} \)の像は、

\( \begin{pmatrix} 1& -1\\ 2 & -2 \end{pmatrix} (\mathbb{R}^2) =\{ c (1,2) \mid c \in \mathbb{R}\}\)

で、基底は\((1,2)\)、その次元は1です。

\((1,−4) \notin \begin{pmatrix} 1& -1\\ 2 & -2 \end{pmatrix} (\mathbb{R}^2) \)なので、対応する線形方程式に解はないです。一方で、\(b= c(1,2) \in \begin{pmatrix} 1& -1\\ 2 & -2 \end{pmatrix} (\mathbb{R}^2) \)のときは、解が存在します。

別の例を考えてみましょう。

\(\begin{pmatrix} 1& -1\\ -2 & 1 \end{pmatrix} (\mathbb{R}^2) = \mathbb{R}^2\)

で、次元は2です。基底としては、行列の行ベクトルから\((1,-1),(-2,1)\)が取れます（線形独立であることを確かめてみてください）。

つまり、この行列を使った線形方程式には、\(b\)がなんであろうが必ず解が存在します。（こういう都合の良い行列を、一般に正則行列という）

ここまでの議論で見てきたように、線形写像の像の次元と、対応する行列の線形独立な列ベクトルの最大本数は一致します。

なぜでしょうか。\(A\)の列ベクトルを\(A=(a_1,\dots, a_N)\)と表すと、\(Ax = x_1 a_1+\cdots +x_N a_N\)です。つまり、像\(A(\mathbb{R}^N)\)とは、\(A\)の列ベクトル\(a_1,\dots,a_N\)によって張られる空間です。空間の次元の定義とは、その空間を生成するベクトルのうち線形独立なものの最大数でした。だから両者の一致がわかるわけです。

像の次元とランクの関係

線形方程式に解があるかどうか調べることは、線形写像の像を調べることに対応していることがわかりました。

実は、この像の次元は、行列のランクと一致しています。

ガウスの消去法を解説した記事では、行列\(A\)のランクとは、\(A\)を階段形に基本変形した\(A \to \begin{pmatrix} I_r & O\\ O &O\end{pmatrix} \)ときに残る単位行列\(I_r\)のサイズ\(r\)、と定義しました。

参考：線形方程式の解き方：ガウスの消去法と基本変形・ランク、LU分解

一方でこの\(r\)は、「ある行列の行ベクトル・列ベクトルのうち、線形独立なものの最大個数」＝像の次元と一致しているのです。

証明について詳しくは：齋藤「線型代数入門」 p.50 [4.2],p.116 [5.1],[5.2],[5.3]

像の次元が、行列のランクと一致しているのはなぜか、大雑把に解説します。

線形写像の次元を\(k\)、行列\(A\)のランクを\(r\)として、\(r=k\)を示す。
(1) 線形写像の像の次元と、対応する行列の線形独立な列ベクトルの最大本数は一致
(2) 行列のうち、線形独立な行ベクトルの最大本数は、行基本変形をしても変わらない
(3)\(A\)の階段形において、線形独立な行ベクトル・列ベクトルは\(r\)本
よって、\(r=k\)

という流れです。

(1)は先ほど示しました。(2)について見てみましょう。行基本変形とは、次の組み合わせでした。

ある行を定数倍する（0倍を除く）
ある行の定数倍を別の行に加える
ある行と別の行を入れ替える

行列\(A\)の行ベクトルを、\(a_1,\dots,a_N\)とします。行の入れ替え操作は、\(a_i\)の番号付け替えに対応しますが、それによって線形独立性は変化しません。例えば、\(a_1,a_2\)が線形独立なら、\(a_2,a_1\)も線形独立です。これらの線形結合は、和を入れ替えることで同じものであることがわかります。そこで、\(a_1,\dots, a_k\)が線形独立であると仮定します。

\(a_1,\dots, a_k\)が線形独立のとき、ある行を定数倍しても、例えば\(ca_1,a_2,\dots, a_k\)は線形独立のままです。\(ca_1,a_2,\dots, a_k\)の線形結合は、\(a_1,\dots, a_k\)の線形結合として見ることができます。（\(ca_1,\dots, a_k\)が線形従属なら、\(a_1,\dots, a_k\)は線形従属。逆もしかり。）

また、\(a_1,\dots, a_k\)が線形独立のとき、ある行を別の行に加えても、例えば\(a_1+a_2,a_2,\dots, a_k\)は線形独立のままです。\(a_1+a_2,a_2,\dots, a_k\)の線形結合は、係数をまとめることで\(a_1,\dots, a_k\)の線形結合として見ることができるので。

よって、(2)行列の基本変形では、線形独立な行ベクトルの本数は変化していないことがわかりました。（基本変形は正則行列によって表わせて、正則行列によってランクは変化しないとも言える）

行列\(A\)を階段形の行列\( \begin{pmatrix} I_r & O \\O&O \end{pmatrix} \)に基本変形します。(3)この階段形の行列で、線形独立なベクトルは\(r\)本です。一方、(1),(2)より、線形独立な行ベクトルの本数\(k\)は変化しないので、\(k=r\)が示せました。

以上によって、