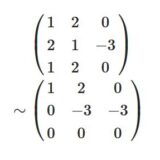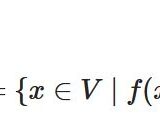線形方程式の解空間とは：基底・基本解、次元の求め方

どうも、木村（@kimu3_slime）です。

今回は、線形方程式（連立一次方程式）の解空間とは何か、基底、次元の求め方を紹介します。

線形方程式の解空間とは
基底、次元の求め方
こちらもおすすめ

線形方程式の解空間とは

次のような線形方程式（連立一次方程式）を考えましょう。

\[ \begin{aligned} x_1+x_2+x_3&=0 \\ 2x_2 +3x_3&=0 \end{aligned} \]

方程式の解\(x=(x_1,x_2,x_3)\)を\(\mathbb{R}^3\)のベクトルと見ます。その解の集合\(W=\{x \mid x は方程式を満たす\}\)を、方程式の解空間（solution space）と呼びます。

線形方程式は、行列によって表すことができます。今回の例ならば、

\[ \begin{aligned} A=\begin{pmatrix}1 &1 &1\\ 0 & 2 &3 \end{pmatrix}\end{aligned} \]

と置くことで、解空間を\(W = \{x \mid Ax=0\}\)と表せます。

解空間が「空間」と呼ばれる理由は、それが必ず部分空間となることによります。

線形方程式を一般に\(Ax=0\)と表し、解空間\(W =\{x \mid Ax=0\}\)と表しましょう。部分空間とは、和とスカラー倍について閉じた集合です。\(x, y \in W\)、\(a \in \mathbb{R}\)とします。行列は線形写像なので、\(A(x+y)=Ax+Ay =0\)、\(Aax = aAx =a0 =0\)が成り立ちました。

線形方程式の解は、（あるとしたら）直線的に広がっているわけです。

基底、次元の求め方

つまり、解空間は線形空間なので、基底と次元が存在します。それを具体的に求めてみましょう。

基底の候補を探す
基底であることを証明する
基底の個数が次元である

\[ \begin{aligned} A=\begin{pmatrix}1 &1 &1\\ 0 & 2 &3 \end{pmatrix}\end{aligned} \]

のとき、基底を探しましょう。一般には、行列を基本変形して単純化すると楽ですが、今回は既に標準形に近い形になっていますね。

そのランクは2です。変数の数は3なので、\(3-2=1\)次元分の不定性があると予想されます。

そこで、\(Ax =0\)の線形独立な解を見つけましょう。\(x_3\)が\(1\)であるような解を探します。

\(x_3 =1\)とすると、\(x_2=-\frac{3}{2}\)で、\(x_1 =\frac{1}{2}\)で、\(a_1 =(\frac{1}{2},-\frac{3}{2},1)\)が見つかります。

（線形独立な解は一通りではないので、自由に見つけて良いです。\(x_1=-1\)であるような解でも、\(x_2=4\)であるような解でも、なんでもOKです。今回は、1つ値を決めれば他の値は決まってしまいます。）

\(a_1\)が基底であることを示しましょう。

線形独立性を示します。\(c_1 a_1 =0\)と仮定すると、\(a_1 \neq 0\)より\(c_1=0\)で、線形独立です。

すべての解\(x=(x_1,x_2,x_3)\)が\(a_1\)の線形結合で表されることを示します。\(x = x_3 a_1\)です。第3成分が等しいのは良いでしょう。第2成分については、方程式を満たしていることから\(-\frac{3}{2}x_3 =x_2\)と等しいことがわかります。第1成分については、\(\frac{1}{2}x_3= -x_3+\frac{3}{2}x_3=-x_3-x_2=x_1\)です。

以上によって、\(a_1\)が解空間\(W\)の基底であるとわかりました。その次元は、\(\mathrm{dim} W =1\)です。

一般に、解空間の基底のことを基本解（fundamental solution）と呼びます。

その定義から、\(Ax=0\)を満たす解はすべて、基本解の線形結合でただ一通りに表せます。

例えば上のケースなら、\(x = x_3a_1\)と表せているわけですね。

基本解は、一般の線形方程式\(Ax =b\)を表すために使われます（一般解＝基本解+特殊解）。

上の例は簡単だったので、もうひとつ例をやって終わりにしましょう。

\[ \begin{aligned} A=\begin{pmatrix} 2&0&1&0 \\ 0&3&2 & -1 \\ -2&3&1&-1 \\ 2 &3& 3 &-1\end{pmatrix} \end{aligned} \]

によって定まる線形方程式\(Ax =0\)の解空間\(W\)の基底、次元を求めたいとします。

行基本変形によって、行列を標準形に近づけ、方程式を単純化しましょう。

\[ \begin{aligned} &\begin{pmatrix} 2&0&1&0 \\ 0&3&2 & -1 \\ -2&3&1&-1 \\ 2 &3& 3 &-1\end{pmatrix} \\& \sim \begin{pmatrix} 2&0&1&0 \\ 0&3&2 & -1 \\ 0&3&2&-1 \\ 0 &3& 2 &-1\end{pmatrix} \\& \sim \begin{pmatrix} 2&0&1&0 \\ 0&3&2 & -1 \\ 0&0&0&0 \\0&0&0&0 \end{pmatrix} \end{aligned} \]

となり、ランクは\(2\)であるとわかりました。変数は\(4\)つで、\(4-2=2\)次元分は自由に決められます。元の方程式は、基本変形によって次のように単純化されました。

\[ \begin{aligned} 2x_1+x_3&=0\\3x_2+2x_3-x_4&=0 \end{aligned} \]

基底を探したいです。つまり、線形独立となるような解を探したいです。そこで、\((x_1,x_2) =(1,0),(0,1)\)であるような解を求めましょう。（線形独立になりさえすれば、どんな形でも良いです）

\((x_1,x_2) =(1,0)\)のときは、\(x_3 =-2\)、\(x_4 =3x_2+2x_3 =-4\)なので、\(a_1 =(1,0,-2,-4)\)と置きます。\((x_1,x_2)=(0,1)\)のときは、\(x_3=0\)、\(x_4=3x_2+2x_3 =3\)なので、\(a_2 = (0,1,0,3)\)と置きます。

\(a_1,a_2\)は方程式の解です。これらが解空間\(W\)の基底であることを示しましょう。

線形独立性について。\(c_1a_1+c_2 a_2 =0\)と仮定すると、第1成分の比較から\(c_1=0\)、第2成分の比較から\(c_2 =0\)が言えます。

すべての解を表せることについて。\(x=(x_1,x_2,x_3,x_4)\)を\(Ax=0\)の解とします。すると、\(x= x_1a_1+x_2 a_2\)と表せます。なぜか。第1、2成分については良いでしょう。方程式を満たすことから、第3成分は\(-2 x_1 +0x_2 =x_3\)です。同様に、第4成分は\(-4x_1+3x_2=3x_2 +2x_3 =x_4\)が成り立ちます。

よって、\(a_1,a_2\)が基底（基本解）であることが言えました。したがって、次元は\(\mathrm{dim}W =2\)です。

一般に、解空間の次元は、変数の個数からランクを引いたものに等しいです。

次元定理によると

\[ \begin{aligned}\mathrm{dim}V= \mathrm{dim} (\ker f) + \mathrm{dim}(f(V))\end{aligned} \]

が成り立ちますが、\(V = \mathbb{R}^n\)、\(f=A\)のときを考えています。

行列の核とは、\(\ker A = \{x \mid Ax=0\}\)なので解空間\(W\)そのものです。また、行列の像の次元は、ランクに等しいです。したがって、

\[ \begin{aligned}n= \mathrm{dim} W + \mathrm{rank}A\end{aligned} \]

が成り立ちます。\(\mathrm{dim} W =n -\mathrm{rank}A \)によって、すぐさま解空間の次元を求めることができるわけです。

この議論を前提とするなら、もし\(\mathrm{rank}A < n\)を示せたら、\(Ax =0\)を満たす\(x \neq 0\)である解が存在すると言えますね。特に\(n -\mathrm{rank}A\)個の基底（基本解）を持ってこれます。

以上、線形方程式の解空間とは何か、基底、次元の求め方を紹介してきました。

線形方程式\(Ax=0\)には、必ず\(x=0\)という自明解が含まれます。\(x \neq 0\)であるような解を持つかは、変数の数\(n\)と方程式の実質的な数\(\mathrm{rank}A\)によって決まるわけです。

今回考えたケースでは、\(\mathrm{rank}A<n \)だったので、方程式には0でない解が存在しました。そういう解がどのくらい広がっているかを表すのが解空間の次元\(n -\mathrm{rank}A\)です。\(n =\mathrm{rank}A\)のときは\(Ax =0\)には自明解\(x=0\)しか存在しなくなります（そういう行列を可逆であると言うのでした）。

すべての解を表すために必要なパラメーターの個数・自由度＝解空間の次元、という見方を、具体的に基底を見つける中で培えると嬉しいですね。

木村すらいむ（@kimu3_slime）でした。ではでは。