行列の対角化可能性の定義とメリット、例、同値条件について解説

どうも、木村（@kimu3_slime）です。

行列の対角化は、線形代数学における大きなテーマのひとつです。

今回は、行列の対角化可能性の定義とメリット、例、同値条件について解説していきます。

対角化可能性の定義、メリット
対角化の例
対角化可能性の条件
- 対角化可能性の同値条件
- 対角化可能性の十分条件
こちらもおすすめ

対角化可能性の定義、メリット

行列の対角化とは、行列を対角行列（対角成分以外が0の行列）に変形することです。

\(A\)を\(N\times N\)の行列とします。\(A\)が対角化可能（diagonalizable）とは、可逆な行列\(P\)、対角行列\(D\)によって\(P^{-1}A P=D\)と表せることです。

ランクを求める基本変形では、基本行列をかけて\(PAQ\)をシンプルと変形しますが、\(P\)と\(Q\)は一般には別物で良いです。一方で、対角化可能性では、\(P^{-1}AP\)と、ある行列\(P\)と\(P^{-1}\)で挟んだ形となっていますね。正則行列による変形という点では同じですが、その目的とする形は違います。

なぜ対角化を考えるかと言えば、行列のべき\(A^k\)が計算しやすいからです。一般に、対角行列のべきは、その対角成分をべき乗すれば良いだけなので、非常に簡単です。

\[ \begin{aligned}D=\begin{pmatrix} d_1 &0& &O \\ 0& d_2 & & \\ &\ddots & \\ O & & &d_N \end{pmatrix}, \quad D^k=\begin{pmatrix} d_1^k &0& &O \\ 0& d_2^k & & \\ &\ddots & \\ O & & &d_N^k \end{pmatrix}\end{aligned} \]

もし行列\(A\)が対角化可能なら、そのべきの計算は簡単になります。\(A=PDP^{-1}\)なので、\(A^2 =PDP^{-1}PDP^{-1}= PDDP^{-1}= PD^2 P^{-1} \)。\(D^2\)は計算しやすいので、\(A^2\)も求められます。同様に一般のべきは、\(A^{k}= PD^k P^{-1} \)となるわけです。

線形常微分方程式系を解くときには、指数行列というものを求める必要がありますが、これも対角化できれば計算が楽になります。

参考：線形常微分方程式を行列で解く：行列の指数関数を解説

対角化の例

では、どんな行列が対角化できるのでしょうか。

もちろん、対角行列は対角化可能です。\(P=E\)と取れば良いだけで、このケースについて考える意味は薄いです。

対角行列でない簡単な例として、\(A= \begin{pmatrix} 1&1\\0&2 \end{pmatrix}\)を考えてみます。

\(AP =PD\)となるような\(P,D\)を探してみましょう。

\(P=(p_1,p_2)\)と列ベクトルを表すと、\(D\)は対角行列なので、\(PD = (d_1 p_1,d_2 p_2)\)です。一方で、\(AP =A(p_1,p_2)= (Ap_1,Ap_2)\)です（行列の積の定義）。

両辺を合わせれば、\(Ap_1 = d_1p_1\),\(Ap_2 =d_2 p_2\)が成り立っています。これはどこかで見たことある形……そう、固有値と固有ベクトルの定義です！

参考：なぜ行列式を学ぶのか？固有値・固有ベクトルの求め方：固有多項式の定義

特性方程式\(p_A(\lambda) =(\lambda -1)(\lambda-2)=0\)を解けば、固有値は1と2。対応する固有ベクトルは\((1,0),(1,1)\)が選べます。

そこで、\(d_1=1,p_1=(1,0)\),\(d_2 =2,p_2=(1,1)\)とします。つまり、\(D=\begin{pmatrix} 1&0\\0&2 \end{pmatrix}\),\(P=\begin{pmatrix} 1&1\\0&1 \end{pmatrix}\)としましょう。

このとき、\(p_1,p_2\)は線形独立なので、\(P\)は可逆です。\(P^{-1}=\begin{pmatrix} 1&0\\-1&1 \end{pmatrix}\)となります。

参考：可逆な行列（正則行列）とは？例と同値な条件

\(AP= PD\)となるように\(D,P\)を定めたので、\(P^{-1} AP =D\)、\(A\)は対角化可能であることがわかりました。

行列を線形ベクトル場として可視化してみます。それは、平面上の点\(x\)の場所に、\(Ax\)で定めるベクトルを描いたものです。固有ベクトルは、ベクトル場の解曲線が直線となるベクトルのこと。

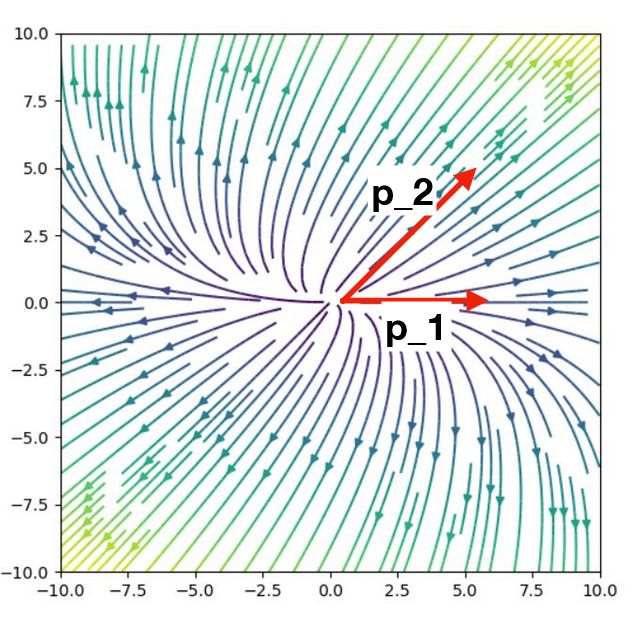
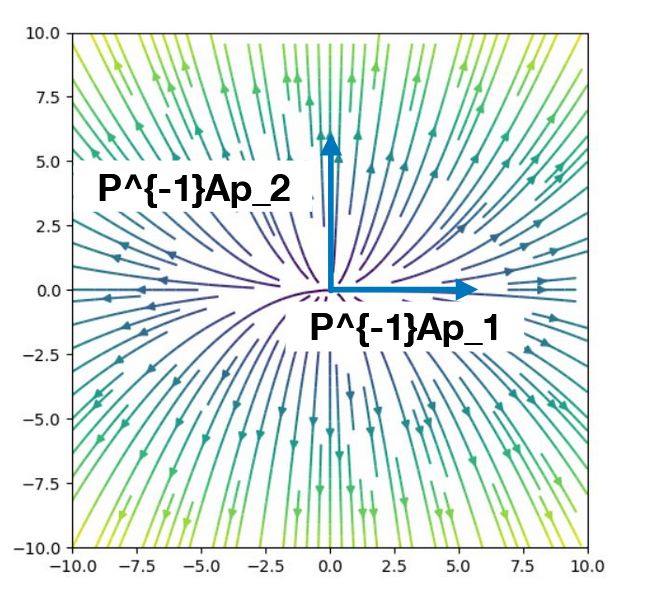
行列の対角化は、固有ベクトル軸が直交して見えるように、\(P\)によって基底を取り直したものと言えます。この基底から見れば、\(A\)が定めるベクトル場は、対角行列が定めるベクトル場です。

別の例を考えてみましょう。\(B= \begin{pmatrix} 1&1\\0&1 \end{pmatrix}\)とします。

同じく固有値と固有ベクトルを調べてみます。特性方程式\(p_A(\lambda) =(\lambda -1)^2=0\)を解けば、固有値は1です。重解のときは、固有値1の重複度は2であるといいます。

固有ベクトルを探すと、\(Bp =p\)なる\(p\)を求めれば、\(p=(c,0)\)の形しかありません。一般に、ある固有値\(\lambda\)に対応する固有ベクトルの張る空間を固有空間\(V_\lambda \)といいます。\(V_{1}=\{(c,0) \mid c \in \mathbb{R}\}\)なので、\(\dim V_1 =1\)です。

つまり、どうやっても固有ベクトル\(p_1,p_2\)を線形独立であるように選ぶことはできません。したがって、対角化は不可能です。

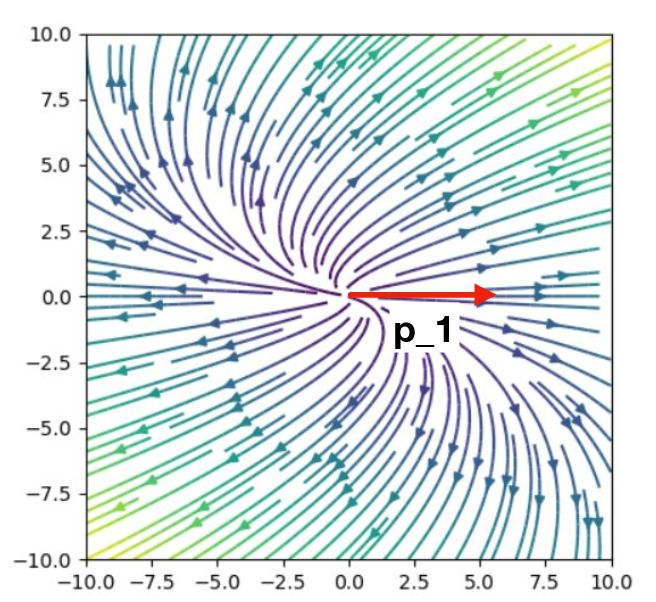
別の言い方をします。仮に対角化可能だったとしましょう（背理法）。上で行った議論と同様にして、\(Bp_1 = d_1p_1\),\(Bp_2 =d_2 p_2\)です。しかし\(B\)の固有値は1しかないのですから、\(d_1=d_2=1\)。つまり、\(P^{-1}AP=I\)です。これを変形すれば\(A=I\)が導かれて矛盾します。

注意をしてほしいのが、\(B\)の固有値が重複していたから対角化できなかったわけではありません。例えば、単位行列\(I\)は固有値1が重複していますが、固有ベクトルは\((1,0),(0,1)\)と線形独立なものが選べるので、対角化可能です。\(B\)が対角化できない原因は、（重複度に対する）固有ベクトルの少なさにあります。

対角化可能性の条件

以上の例によって、対角化できる行列とできない行列の違いがわかってきました。固有ベクトルを\(P\)が可逆行列となるように選べるかどうか、それが違いを生み出しています。

対角化可能性の同値条件

\(A\)を\(N\times N\)の行列とする。\(A\)が対角化可能であることは、\(A\)が\(N\)個の線形独立な固有ベクトルを持つことと同値。
（対角化可能ならば、\(P\)は\(A\)の固有ベクトルを、\(D\)は\(A\)の固有値を並べた行列となる。）

\(A\)が対角化可能、\(P^{-1} AP =D\)とします。このとき、\(AP =PD\)です。\(P=(p_1,\dots, p_N)\)と表せば、\(Ap_1 =d_1 p_1,\dots,Ap_N= d_Np_N\)が得られます。\(P\)は可逆行列なので、\(p_k \neq 0\)。つまり、これらは固有ベクトルの定義式なので、\(d_k\)は\(A\)の固有値、\(p_k\)は\(A\)の固有ベクトルです。\(P\)は可逆行列なので、その列ベクトルは線形独立、すなわち\(A\)が\(N\)個の線形独立な固有ベクトルを持ちます。

逆に、\(A\)が\(N\)個の線形独立な固有ベクトルを持つとしましょう。それらを\(p_1,\dots,p_k\)、対応する固有値を\(d_1,\dots,d_N\)と表し、それにより\(P,D\)を定義します。固有ベクトルの定義より、\(Ap_1 =d_1 p_1,\dots,Ap_N= d_Np_N\)が成り立つので、\(AP =PD\)です。線形独立なベクトルを並べてできる行列は可逆なので、\(P\)は可逆です。よって、\(P^{-1} AP =D\)、\(A\)は対角化可能であることが示せました。

（この同値条件は、\(A\)のすべての固有値の重複度が固有空間の次元に等しい \(m_k = \dim V_{\lambda _k}\) とも言えます。）

対角化可能性の十分条件

とはいえ、固有ベクトルが線形独立となるよう選べるかを調べるのは、面倒くさいです。そこで、次のような条件が知られています。

\(A\)の固有値がすべて異なるならば、\(A\)は対角化可能である。

これは「異なる固有値に対応する固有ベクトルは、線形独立である」という事実に支えられています。

確かめてみましょう。\(A\)の固有値を\(\lambda _1,\dots, \lambda _N\)、固有ベクトルを\(x_1,\dots, x_N\)として、数学的帰納法によって示します。

\(x_1\)は固有ベクトルなので、\(x_1 \neq 0\)であり、線形独立です。

\(\{x_1,\dots,x_k\}\)が線形独立であると仮定します。\(c_1 x_1 +\cdots+c_k x_k +c_{k+1}x_{k+1}=0\) (1) という関係が成り立ったとしましょう。(1)の両辺に\(\lambda_ {k+1}\)をかければ、

\[ \begin{aligned}c_1 \lambda_{k+1} x_1 +\cdots+c_k \lambda_{k+1} x_k +c_{k+1} \lambda_ {k+1}x_{k+1}=0\end{aligned} \]

です。一方で、(1)に\(A\)をかけて、線形性を使って整理すると

\[ \begin{aligned}c_1 \lambda_1 x_1 +\cdots+c_k \lambda_k x_k +c_{k+1} \lambda_ {k+1} x_{k+1}=0\end{aligned} \]

です。この2つの式を引くと、

\[ \begin{aligned}c_1 (\lambda_{k+1} -\lambda_1) x_1 +\cdots+c_k (\lambda_{k+1} -\lambda_k )x_k =0\end{aligned} \]

ですが、\(\{x_1,\dots,x_k\}\)の線形独立性より、\(c_1 (\lambda_{k+1} -\lambda_1) = \cdots =c_k(\lambda_{k+1} -\lambda_k) =0\)です。固有値はすべて異なっていたので、\(\lambda _{k+1} – \lambda_i\neq 0\)であり、\(c_1=\cdots =c_k=0\)となります。

よって、式(1)は\(c_{k+1}x_{k+1}=0\)です。\(x_{k+1}\)は固有ベクトルなので\(x_{k+1}\neq 0\)で、\(c_{k+1}=0\)。\(\{x_1,\dots,x_k,x_{k+1}\}\)が線形独立であることが示せました。

以上、対角化可能性の定義とメリット、例、対角化の同値な言い換えと十分条件を紹介してきました。

対角化可能性を考えれば、固有値・固有ベクトルの定義式があの形になっているのも納得していただけるのではないでしょうか。ぜひ、行列の対角化と固有ベクトルの関係について、結びつけながら理解していってください。

木村すらいむ（@kimu3_slime）でした。ではでは。