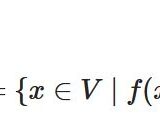共通部分、和空間の次元の等式とは、その証明

どうも、木村（@kimu3_slime）です。

線形空間の部分空間の共通部分、和空間の次元に関する等式と、その証明を紹介します。

共通部分、和空間の次元の等式
部分空間の次元等式の証明
こちらもおすすめ

共通部分、和空間の次元の等式

\(V\)を有限次元の線形空間、\(W_1,W_2\)をその部分空間とします。すると、その共通部分\(W_1\cap W_2\)と和空間\(W_1+W_2\)は部分空間です。さらにその次元については、

\[ \begin{aligned}\dim(W_1+W_2)=\dim W_1 +\dim W_2 -\dim (W_1 \cap W_2)\end{aligned} \]

が一般に成り立ちます。

具体例：部分空間の基底、次元の求め方（生成、共通部分、和空間）

有限集合\(A,B\)の要素の個数について、その個数を\(\mathrm{card}A\)と表すとき、

\[ \begin{aligned}\mathrm{card}(A\cup B) = \mathrm{card}A +\mathrm{card}B – \mathrm{card}(A\cap B)\end{aligned} \]

が成り立つのに似ています。バラバラに足してから、重複している部分を引けば良い、と。

ただし、部分空間の次元等式では、単なる和集合ではなく、和空間\(W_1+ W_2 =\{x+y \mid x \in W_1 ,y \in W_2\}\)を考えていることに注意しましょう。

部分空間の次元等式の証明

では、等式

\[ \begin{aligned}\dim(W_1+W_2)=\dim W_1 +\dim W_2 -\dim (W_1 \cap W_2)\end{aligned} \]

を証明しましょう。

包含関係としては、\(W_1 \cap W_2 \subset W_1,W_2 \subset W_1 +W_2\)が成り立っています。\(V\)は有限次元なので、これらも有限次元です。包含関係から、\(\dim (W_1 \cap W_2) \leq \dim W_1, \dim W_2 \leq \dim (W_1+W_2)\)が成り立っています。

そこで、\(\dim(W_1 \cap W_2) = p\)、\( \dim W_1 =p+q\)、\(\dim W_2 =p+r\)と置いたとき、\(\dim (W_1+W_2)=p+q+r\)を示せば良いです。

\(W_1 \cap W_2\)の基底を\(a_1,a_2,\dots ,a_p\)としましょう。\(a_1,\dots,a_p\)は、\(W_1,W_2\)の要素でもある線形独立なベクトルです。そこで、それらにいくつかの要素を加えて、\(W_1,W_2\)の基底が作れます。\(a_1,\dots,a_p,b_1,\dots,b_q\)を\(W_1\)の基底、\(a_1,\dots,a_p,c_1,\dots,c_r\)を\(W_2\)の基底としましょう。（\(a_1,\dots,a_p\)の張る空間を考え、それが\(W_1\)に一致していなかったら、一致してない部分から基底の候補\(b_1\)を選んで加える。それは\(\dim W_1\)個になるまで繰り返せる。\(W_2\)についても同様。）

結論としては、\(a_1,\dots,a_p,b_1,\dots,b_q,c_1,\dots,c_r\)が\(W_1 +W_2\)の基底であることを示せば良いです。その個数は\(p+q+r\)個なので。

\(a_1,\dots,a_p,b_1,\dots,b_q \in W_1\)、\(c_1,\dots,c_r \in W_2\)なので、和空間の定義から\(a_1,\dots,a_p,b_1,\dots,b_q,c_1,\dots,c_r \in W_1 +W_2\)が成り立ちます。

線形独立性について。

\(\sum_{i=1} ^p x_i a_i+ \sum_{j=1}^q y_jb_j +\sum_{k=1}^r z_kc_k=0\)と仮定します。移行すると\(\sum_{i=1} ^p x_i a_i+ \sum_{j=1}^q y_jb_j = – \sum_{k=1}^r z_kc_k\)です。ここで、左辺は\(W_1\)の要素の線形結合なので\(W_1\)の要素であり、右辺は\(W_2\)の要素の線形結合なので\(W_2\)の要素となります。したがって、\(W_1\)の要素でありかつ\(W_2\)の要素である、すなわち\(W_1 \cap W_2\)の要素です。

右辺を\(W_1 \cap W_2\)の基底によって、\(- \sum_{k=1}^r z_kc_k = \sum_{i=1}^p w_i a_i\)と表しましょう。元の等式に戻すと、\(\sum_{i=1} ^p (x_i -w_i)a_i+ \sum_{j=1}^q y_jb_j =0\)です。\(a_1,\dots,a_p,b_1,\dots,b_q\)は\(W_1\)の基底なので、線形独立性によって、\(x_i -w_i =0\)、\(y_j =0\)となります。

再び元の等式に戻ると、\(\sum_{i=1} ^p x_i a_i +\sum_{k=1}^r z_kc_k=0\)です。\(a_1,\dots,a_p,c_1,\dots,c_r\)は\(W_2\)の基底なので、線形独立性によって、\(x_i =0\)、\(z_k =0\)。以上によって、すべて係数が0となることがわかりました。

\(W_1,W_2\)を生成していること。

任意に\(w \in W_1 +W_2\)を選ぶと、和空間の定義から\(w= x+y\)、\(x\in W_1, y \in W_2\)と表せます。\(a_1,\dots,a_p,b_1,\dots,b_q\)は\(W_1\)の基底なので、線形結合として\(x=\sum_{i=1} ^p x_i a_i+ \sum_{j=1}^q y_jb_j \)と表せます。同様に\(W_2\)の基底を使えば、\(y=\sum_{i=1} ^p w_i a_i +\sum_{k=1}^r z_kc_k\)と表せます。よって、\(w=\sum_{i=1} ^p (x_i+w_i) a_i+ \sum_{j=1}^q y_jb_j +\sum_{k=1}^r z_kc_k \)と線形結合で表せました。

以上により\(p+q+r\)個の基底の存在が言えたので、次元の等式が証明できました。

今回は、部分空間の共通部分、和空間の次元の等式と、その証明を紹介してきました。

特に、共通部分が0次元 \(\dim (W_1 \cap W_2)=0\) のときは、

\[ \begin{aligned}\dim(W_1+W_2)=\dim W_1 +\dim W_2\end{aligned} \]

という等式が成り立つわけです。このとき和空間\(W_1 +W_2\)は直和であると呼ばれます。

このように、部分空間の直和について学ぶ上でも、今回示した等式は基本的です。中身としても素直に定義に戻って議論すれば示せる内容なので、恐れずに等式を活用してみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。