どうも、木村(@kimu3_slime)です。
今回は、直交補空間、直交直和、直交射影とは何か、定義と例、証明について紹介します。
前提知識:部分空間の直和とは:定義と例、射影
部分空間の直交補空間
例
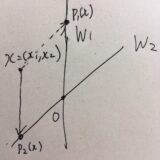
線形空間として、\(V = \mathbb{R^2}\)という平面を考えましょう。
これに対して、\(W_1 =\{x \mid x_2 =0\}\)、\(W_2 = \{x \mid x_1 =0\}\)と置くと、これらは1次元の部分空間(直線)です。
部分空間に対しては、その和空間を考えることができました。この例では、\(W_1 +W_2 = \mathbb{R}^2\)となります。さらに、\(x= (x_1,x_2)= (x_1,0)+(0 ,x_2)\)と分解できるので、この和は直和\(\mathbb{R}^2 = W_1 \dot{+} W_2\)です。
中学校の座標平面で学ぶ、いわゆる\(x,y\)軸が直交している状態を表していますね。
2つの部分空間\(W_1,W_2\)が直交していることを正確に言えば、すべての\(x \in W_1\)と\(y \in W_2\)に対して、内積が0 \(\langle x,y\rangle =0\) となることです。
今回の例では、\(x=(x_1,0)\)、\(y=(0,y_1)\)なので、\(\langle x,y\rangle =0\)で、直交していることが見て取れます。
直和であるからといって、必ず直交しているとは限りません。
例えば、\(W_3 =\{x \mid -x_1 +x_2 =0\}\)とすると、\(W_1\)と\(W_3\)は直交していません。
\(x=(1,0) \in W_1\)と\( y=(1,1) \in W_3\)の内積を計算すれば、\(\langle x,y\rangle= 1 \neq 0\)となるので。
ひとつ部分空間があったときに、それに対して直交するような部分空間が、直交補空間です。
\(W_3\)に対する直交補空間\(W_4\)を求めてみましょう。
\(W_3\)の任意の要素は、\((x_1,x_1)\)と表せます。\(W_4\)の要素を\((y_1,y_2)\)とすると、それらが直交するということは、\(\langle x,y\rangle = x_1(y_1+y_2)=0\)がいつでも成り立つことです。つまり、\(y_1+y_2=0\)でなければならない。
すなわち、\(W_4 =\{y \mid y_1+y_2 =0\}\)と置けば、\(W_3\)と\(W_4\)は直交しています。
定義
以上のことを一般化してまとめましょう。\(V\)を内積を持った線形空間(内積空間)で、有限次元とします。
2つの部分空間\(W_1,W_2\)が直交している(orthogonal, perpendicular)とは、すべての\(x \in W_1\)と\(y \in W_2\)に対して、内積が0 \(\langle x,y\rangle =0\) となることです。このとき、\(W_2 =W_1^{\perp} \)と書きます。
また、部分空間\(W_1\)に対して、\(W_1\)と直行するような部分空間が必ず存在します。それを直交補空間(orthogonal complement space)と呼び、\(W_1^{\perp}\)と表します。つまり、
\[ \begin{aligned}W_1 ^{\perp} := \{y \mid すべてのx\in W_1 に対し、\langle x,y\rangle =0\}\end{aligned} \]
です。
\(W_1^{\perp}\)が部分空間であることを確かめてみましょう。
\(y,z \in W_1 ^{\perp}\)、スカラー\(a \)を任意のものとします。さらに\(x \in W_1\)を任意とし、直交性を確かめましょう。内積の線形性より、\(\langle x,y+z\rangle =\langle x,y\rangle+ \langle x,z\rangle =0\)なので、\(y+z \in W_1 ^{\perp}\)です。また、再び内積の線形性より、\(\langle x,ay\rangle =a\langle x,y\rangle =0\)なので、\(ay\in W_1 ^{\perp}\)が言えました。
さらに、部分空間とその直交補空間は直和になっています \(V =W_1 \dot{+}W_1^{\perp}\)。
これも確かめてみましょう。
\(W_1, W_1 ^{\perp}\)なので、\(W_1+W_1^{\perp} \subset V\)です。逆の包含関係を示したい。つまり、\(V\)の任意の要素を、\(x= y+z\)、\(y \in W_1, z \in W_1 ^{\perp}\)と和で表したいです。
そこで基底を利用します。\(V\)は内積空間なので、正規直交基底が存在します(シュミットの直交化法)。\(W_1\)の正規直交基底を、\(e_1,\dots,e_k\)とします。
\(y: = \sum_{i=1}^k \langle x,e_i\rangle e_i\)と置きましょう。これは\(x\)の\(e_i\)への射影です。そして\(z= x-y\)と置きます。当然\(x=y+z\)にはなります。
\(y\)は\(W_1\)の基底の線形結合なので、\(y \in W_1\)です。\(y,z\)が直交していることを確かめましょう。内積の線形性、正規直交基底であることを使えば、
\[ \begin{aligned} \langle y,z\rangle &= \langle \sum_{i=1}^k \langle x,e_i\rangle e_i,x -y\rangle \\ &=\sum_{i=1}^k \langle x,e_i\rangle ( \langle e_i,x \rangle – \langle e_i,y \rangle)\\ &=\sum_{i=1}^k \langle x,e_i\rangle ( \langle e_i,x \rangle – \langle x,e_i \rangle \langle e_i,e_i \rangle) \\ &= 0 \end{aligned} \]
と言えました。よって、\(V =W_1 +W_1^{\perp}\)です。
さらに直和であること、\(W_1 \cap W_1 ^{\perp}=\{0\}\)を示します。部分空間の共通部分なので、\(W_1 \cap W_1 ^{\perp} \supset \{0\}\)は良いでしょう。
\(x \in W_1 \cap W_1 ^{\perp}\)を任意の要素とします。直交補空間の定義から\(\langle x,x\rangle =0\)が成り立つわけですが、内積の正定値性から\(x=0\)です。以上より、部分空間とその直交補空間は直和になっていることが言えました。
一般に、部分空間\(W_1 ,W_2\)が直交していて、かつ\(V\)がそれらの直和になっているとき、その和を直交直和(orthogonal direct sum)と呼びます。そして、\(V = W_1 \oplus W_2\)と表します。(\(V= W_1 \perp W_2\)と書くこともあるようです)
直交補空間については、必ず\(V = W_1 \oplus W_1 ^{\perp}\)となるわけです。
次元
直和の次元については、共通部分の次元が0なので、
\[ \begin{aligned}\dim(W_1\dot{+}W_2)=\dim W_1 +\dim W_2 \end{aligned} \]
という単純な等式が成り立ちました。
これを\(W_1\)とその直交補空間\(W_2 = W_1 ^{\perp}\)にあてはめて整理すれば、
\[ \begin{aligned}\dim W_1 ^{\perp}=\dim V -\dim W_1 \end{aligned} \]
となります。直交補空間は、部分空間\(W_1\)において全体から不足した次元を補うだけの次元があるわけです。
例えば、\(\mathbb{R}^3\)において、直線からなる部分空間の直交補空間は平面になります。
直交射影
線形空間を直和分解できると、それに伴って成分分解、射影が存在しするのでした。
今回の議論から、部分空間\(W_1\)があると、\(v \in V\)に対し、\(v =x+y\)、\(x\in W_1, y \in W_1 ^{\perp}\)と一通りに表せます。そこで、
\[ \begin{aligned}P_1 (v) := x\end{aligned} \]
\[ \begin{aligned}P_2 (v) := y\end{aligned} \]
と写像\(P_1,P_2 :V \to V\)を定めましょう。これを部分空間\(W_1,W_1 ^{\perp}\)への射影と呼びます。
特に、\(P_1\)を\(W_1\)への直交射影(orthogonal projection)、正射影と呼びます。\(W_1 \)と\(W_1 ^{\perp}\)は直交しているので、それぞれの射影\(P_1 (v),P_2 (v) \)は必ず直交しています。
\(V= \mathbb{R}^2\)において、\(W_3 =\{x \mid -x_1 +x_2 =0\}\)への直交射影を具体的に考えましょう。直交補空間は、\(W_3 ^{\perp}=W_4 =\{y \mid y_1+y_2 =0\}\)です。
\(W_3\)は1次元で、正規直交基底を\(e_1 \)とします(例えば、\(e_1 =\frac{1}{\sqrt{2}}(1,1)\))。\(x=(x_1,x_2)\)の\(e_1\)への射影は、\(\langle x,e_1\rangle e_1 \)です。確かに、\((x_1,x_2) = \langle x,e_1\rangle e_1+(x- \langle x,e_1\rangle e_1)\)と置けば良いので。
\[ \begin{aligned} P_1 (x) &= \langle x,e_1\rangle e_1 \\ &=\frac{1}{2}(x_1+x_2,x_1+x_2) \end{aligned} \]
\[ \begin{aligned} P_2 (x) &= x- \langle x,e_1\rangle e_1 \\&= \frac{1}{2}(x_1-x_2,-x_1+x_2)\end{aligned} \]
が射影です。
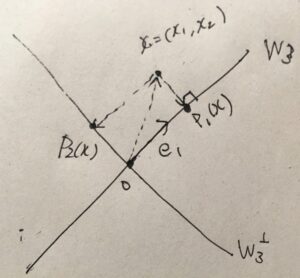
確かに、\(W_3\)への射影\(P_1 (x)\)と、直交補空間への射影\(x-P_1(x)= P_2(x)\)は直交していますね。
この場合は、正射影を求めることは、ある点から直線への垂線の足(交点)を求める問題と言えます。
以上、直交補空間、直交直和、直交射影について、定義と例、証明を紹介してきました。
空間に内積が定まっていると、直和のように単に成分を分解できるだけでなく、直交した座標を使って成分が分解できます。その応用としては、直交行列による対称行列の対角化や最小二乗法、(少し事情が違いますが)フーリエ級数展開などがあります。
ユークリッド空間で直交座標を考えるのはとても便利ですが、それを一般化したものとして直交補空間の考え方があることを知ってもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
共立出版 (1982-07-09T00:00:01Z)
¥788 (中古品)
世界標準MIT教科書 ストラング:線形代数イントロダクション
近代科学社 (2015-12-22T00:00:01Z)
¥14,721 (コレクター商品)
東京大学出版会 (2019-03-08T00:00:00.000Z)
¥1,870
こちらもおすすめ
線形代数の応用:関数の「空間・基底・内積」を使ったフーリエ級数展開