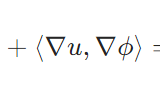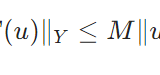線形作用素・汎関数とは：行列、積分作用素、微分作用素の例

どうも、木村（@kimu3_slime）です。

今回は、線形作用素・汎関数とは：行列、積分作用素、微分作用素の例を紹介します。

線形作用素とは
こちらもおすすめ

線形作用素とは

導入

作用素（operator）とは、関数や数列を、別の関数や数列、数に対応させる対応関係（写像）のことです。

例えば、\(F_1 : L^1((0,1))\to \mathbb{R}\) を

\[F_1 (u) := \int_0 ^1 u(x)dx\]

によって定めましょう。可積分な関数\(u \in L^1\)に対して、その値＝積分結果\(F(u) \in \mathbb{R}\)が定まります。特に、\(u(x)=x^2\)のときを計算してみると、

\[F_1 (u) = \int_0^1 x^2 dx = \frac{1}{3}\]

ですね。

積分を使って定義される作用素全般は、積分作用素（integral operator）と呼ばれます。

関数の変数や値を、数や（有限次元の）ベクトルに限らないように、一般化したものと言えます。

定義

一般に、ノルム空間\(X,Y\)において、写像\(F:X\to Y\)を考えましょう。

\(F\)が線形作用素（linear operator）であるとは、

線形性：どんな\(u,v \in X\)、スカラー\(\lambda \)に対しても、\(F(\lambda u +v)=\lambda F(u)+F(v)\)が成り立つ

を満たすことです。

この定義は、線形写像と全く同じことを意味します。慣例の話にすぎませんが、有限次元の空間を考えるときは線形写像、無限次元の空間を考えるときは線形作用素と呼ぶことが多いですね。

したがって、線形写像の簡単な例として、行列があります。\(N\times N\)の行列\(A\)は、\(A(\lambda x+y)=\lambda Ax +Ay\)という線形性を持つ、\(A:\mathbb{R}^N \to \mathbb{R}^N\)という線形写像です。

例

また、さきほどの積分作用素\(F_1\)は線形作用素です。定義域は\(X= L^1((0,1))\)、余定義域は\(Y=\mathbb{R}\)ですね。そして、積分の線形性から

\[\begin{aligned} &F_1(\lambda u +v) \\ &= \int _0^1 (\lambda u(x)+v(x))dx \\&= \lambda \int_0^1 u(x)dx +\int_0^1 v(x)dx \\&= \lambda F_1(u)+F_1(v) \end{aligned}\]

となるので。

値（余定義域）が数であるような線形作用素は、線形汎関数（linear functional）とも呼ばれます。関数解析（functional analysis）という分野は、主に積分作用素といった汎関数の分析から始まりました。

\(F_2: C^1([0,1])\to C^0([0,1])\)を

\[F_2 (u):=\frac{du}{dx} \]

により定めましょう。\(C^k\)は微分可能な関数のなす空間です。微分を含む作用素を、微分作用素（differential operator）と呼びます。

さきほどの積分作用素は「関数→実数」の対応でしたが、微分作用素は「関数→関数」という対応になっていることに注意しましょう。例えば、\(u(x)=x^2\)のとき、その「値」\(F_2(u)=2x\)は関数です。

これを\(F_2(x^2)=2x\)と書く記法では、\(F_2\)の変数が何なのか注意しましょう。ここでは変数は\(x^2\)という関数です。（変数ではない数）\(x=1\)を「代入」して\(F_2(1) = 2\)と考えるのは間違いです。実際、定数関数\(u(x) \equiv 1\)について、その微分は0 \(F_2 (1)=0\)なので。

積分と同様に、微分は線形性を持つため、

\[\begin{aligned} &F_2(\lambda u +v) \\ &= \frac{d}{dx}(\lambda u +v) \\&= \lambda \frac{du}{dx}+ \frac{dv}{dx} \\&= \lambda F_2(u)+F_2(v) \end{aligned}\]

となり、線形作用素です。

当然のことですが、すべての作用素（対応関係）が、線形であるわけではありません。線形でない作用素は、非線形作用素（nonlinear operator）と呼ばれます。

行列\(A\)により決まる二次形式\(F_3: \mathbb{R}^N \to \mathbb{R}\)、\(F_3 (x): = \langle x, Ax \rangle\)は、必ずしも線形作用素ではありません。

\[F_3 (\lambda x) = \langle \lambda x , A(\lambda x)\rangle \\= \lambda ^2 \langle x, Ax\rangle = \lambda ^2F_3(x)\]

なので、例えば\(A\)が正定値行列で、\(x \neq 0\)ならば、\(\langle x, Ax \rangle \neq 0\)で、\(F_3(2x) = 4F_3(x ) \neq 2F_3(x) \)なので、線形作用素ではありません。

積分を用いた例としても、\(F_4(u)= |\int_0^1 u(x) dx|\)を考えましょう。これも線形作用素ではありません。

\(u(x) = 1\)について考えると、\(F_4(u)=1\)、\(F_4(-u)=|-1|=1\)で、\(F_4(u) = F_4(-u) \neq -F_4(u)\)となるので。

微分を用いた線形でない作用素の例も考えてみてください。

以上、線形作用素とは：積分作用素、微分作用素、簡単な例を紹介してきました。

線形作用素のうち、有界な線形作用素が特に重要です。偏微分方程式の分析において、コンパクト作用素や双対空間は重要ですが、その基礎として有界線形作用素があります。これについては、別記事にて。

今回はその初歩、関数に対して数や関数を対応させる作用素という視点、さらにそのうち線形であるものに注目する線形作用素という考え方が伝われば嬉しいです。

木村すらいむ（@kimu3_slime）でした。ではでは。