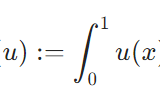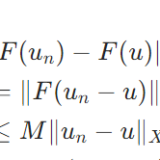どうも、木村(@kimu3_slime)です。
今回は、有界線形作用素、ノルムとは:行列、積分作用素、微分作用素の例を紹介します。
有界線形作用素とは
定義
有界線形作用素は、線形作用素のうち、有界性という良い性質を持ったものです。
\(X,Y\)をノルム空間、\(F:X\to Y\)を線形作用素とします。
\(F\)が有界線形作用素(bounded linear operator)とは、「すべての\(u \in X\)に対し、\(\|F(u)\|_Y \leq M \|u\|_X\)」を満たす\(M\)が存在することです。
取りうる値が数 \(Y = \mathbb{R}\) のとき、\(F\)は有界線形汎関数(bounded linear functional)と呼ばれます。
それぞれ有界作用素、線形汎関数といった省略した呼び方をすることもあります。その文脈においては、線形性、有界性は当たり前のものとされていることに注意しましょう。
行列
簡単な例として、\(X=Y=\mathbb{R}^2\)
\[A= \begin{pmatrix} -1&0 \\0 &2 \\\end{pmatrix}\]
という対角行列を考えましょう。
\(u=(x,y)\)とし、\(\|Au\|_{\mathbb{R}^2} \leq M \|u\|_{\mathbb{R}^2}\)を満たす\(u\)に依存しない\(M\)を探したいわけですが、そのためにまず\(\|Au\|\)を計算します。
\[Au = \begin{pmatrix} -x\\ 2y \\\end{pmatrix}\]
となるので、ここから\(\|u\|_{\mathbb{R}^2}\)の定数倍が作り出せるように評価すれば、
\[\begin{aligned} &\|Au\|_{\mathbb{R}^2}^2 \\ &= x^2 +4y^2 \\ & \leq 4x^2+4y^2 \\&= 4 \|u\|_{\mathbb{R}^2}^2 \end{aligned}\]
となるので、平方根を取れば
\[\|Au\|_{\mathbb{R}^2} \leq 2 \|u\|_{\mathbb{R}^2}\]
です。\(M=2\)は\(u\)に依存せず、\(A\)の有界性が示せました。
一般の行列に対しても、行列の作用素ノルム\( \begin{aligned}\|A\| = \max_ {x \in \mathbb{R}^n \\ x \neq 0} \frac{\|Ax\|_{\mathbb{R}^m}}{\|x\|_{\mathbb{R}^n}}\end{aligned} \)により、\(M =\|A\|\)と置けば、必ず\(A\)は有界となります。
積分作用素
積分作用素として、\(F_1 :L^1((0,1)) \to \mathbb{R}\)
\[F_1 (u) = \int_0^1 u(x)dx\]
を考えましょう。
\(\mathbb{R}\)のノルム(ユークリッドノルム)は、絶対値となります。
積分の三角不等式より、
\[\begin{aligned} & |F_1(u)|\\ &=| \int_0^1 u(x)dx| \\& \leq \int_0^1 |u(x)|dx \\ &= \|u\|_{L^1} \end{aligned}\]
となるので、\(M=1\)として\(F_1\)は有界線形作用素です。
微分作用素
すべての線形作用素が、有界であるわけではありません。非有界になりうる典型例として、微分作用素が知られています。
\(F_2 : C^1([0,1]) \to C^0 ([0,1])\)
\[F_2 (u) = \frac{du}{dx}\]
について考えましょう。ただし、定義域、余定義域ともにノルムは上限ノルム\(\|u\|_{C^0}= \max_{x \in [0,1]} |u(x)|\)とします。
\(a>0\)として\(u(x)=e^{ax}\)について考えましょう。\(u \in C^1([0,1])\)です。
\[\begin{aligned} & \|F_2(u)\|_{C^0}\\ &= \max_{x \in [0,1]} |ae^{ax}| \\ &= a e^{a} \\&= a \max_{x \in [0,1]} |e^{ax}| \\ &= a \|u\|_{C^0}\end{aligned}\]
となります。さきほどまでの例と違い、\(a\)は\(u\)に依存していて、かついくらでも大きく選ぶことができます。
どんな実数\(M\)に対しても、\(\|F_2(u)\|_{C^0}=(M+1)\|u\|_{C^0} > M\|u\|_{C^0}\)を満たす\(u\)が存在します(\(u(x)=e^{(M+1)x}\))。よって、\(F_2\)は有界ではありません。
ともに\(L^2\)ノルムを用いても、同様にして有界ではありません。
また、\(C^1\)ノルム、\(C^0\)ノルムを合わせると有界になります。\(C^1\)ノルムとは
\[\|u\|_{C^1} = \max_{x \in [0,1 ]} |u(x)|+\max_{x \in [0,1 ]} |\frac{du}{dx}(x)| \]
のことです。これを用いれば、
\[\begin{aligned} &\|F_2(u)\|_{C^0} \\ &=\max_{x \in [0,1 ]} |\frac{du}{dx}(x)| \\&\leq \max_{x \in [0,1 ]} |u(x)|+\max_{x \in [0,1 ]} |\frac{du}{dx}(x)| \\&= \|u\|_{C^1} \end{aligned}\]
となるので、\(F_2\)は有界です。
作用素が有界であることは、表示式だけから決まることではなく、考える定義域・余定義域やそれらのノルム次第であることに注意しましょう。微分作用素は一般には非有界ですが、必ず非有界というわけでもありません。
像の有界性
これまで見てきたことからすぐにわかるのは、有界作用素による像は大きくなりすぎないということです。
もし\(F: X\to Y\)が有界作用素で、\(B\subset X\)が有界集合ならば、その像\(F(B)\)は有界集合です。
\(B \subset B(0,R)\)という半径\(R\)の球に含まれるとしましょう。\(u \in B\)として、\(\|F(u)\| \leq M \|u\| \leq MR\)なので、\(F(B) \subset B(0,MR)\)となるため、像\(F(B)\)は有界集合です。
重要な性質として、線形作用素について、有界であることと連続であることは同値であることが知られています。
有界線形作用素は連続線形作用素でもあり、逆もしかりというわけです。これについては別記事で。
作用素のノルム
定義
有界線形作用素のなす集合\(B(X,Y)\)は、適当に和とスカラーを定義することで、線形空間となります。
さらに、作用素\(F: X \to Y\)に対し、
\[\|F\|_{B(X,Y)}:= \inf \{M \mid \\すべてのu\in Xに対し \|F(u)\|_{Y} \leq M\|u\|_{X}\}\]
と下限を使って定義すると、\(\|\cdot\|_{B(X,Y)}\)は\(B(X,Y)\)上のノルムになります。これを作用素ノルム(operator norm)と呼びます。
\(X \neq \{0\}\)のとき、作用素ノルムの同値な定義として、
\[\|F\|_{B(X,Y)}= \sup_{u \neq 0} \frac{\|F(u)\|_{Y}}{\|u\|_{X}} = \sup _{\|u\|_{X} =1} \|F(u)\|_Y\]
が知られています。\(F\)の作用素ノルムは、\(F\)の拡大倍率の上限のようなものです。
行列
作用素ノルムをいくつか計算してみましょう。
\[\|F\|_{B(X,Y)}= \sup_{u \neq 0} \frac{\|F(u)\|_{Y}}{\|u\|_{X}}\]
という形が扱いやすいです。上限を求めるには、
- 上限の値\(K\)に予想をつけて
- \(K\)が実際に上限であることを証明する(\(K\)は上界、かつ最小の上界であること)
という流れを取ります。前提として、上限の定義や示し方を知っておく必要があるでしょう。
\[Au = \begin{pmatrix} -x\\ 2y \\\end{pmatrix}\]
については、常に
\[\|Au\|_{\mathbb{R}^2} \leq 2 \|u\|_{\mathbb{R}^2}\]
となるので、\( u \neq 0\)ならば
\[ \frac{\|Au\|_{\mathbb{R}^2}}{\|u\|_{\mathbb{R}^2}} \leq 2 \]
したがって、\(2\)は\(\{\frac{\|Au\|_{\mathbb{R}^2}}{\|u\|_{\mathbb{R}^2}} \mid u \neq 0\}\)の上界です。
さらに、\(u=(0,1)\)とすれば、\(Au=(0,2)\)なので、
\[\begin{aligned}&\frac{\|Au\|_{\mathbb{R}^2}}{\|u\|_{\mathbb{R}^2}}\\& = \frac{\sqrt{0^2+2^2}}{\sqrt{0^2+1^2}}\\&= \frac{2}{1}\\&=2 \end{aligned}\]
を満たす\( u \neq 0\)が存在します。これが最大値で、最大値が存在するときはそれは上限と一致します。よって、
\[\begin{aligned} & \|A\|_{B(\mathbb{R}^2,\mathbb{R}^2)}\\ &= \sup_{u \neq 0} \frac{\|Au\|_{\mathbb{R}^2}}{\|u\|_{\mathbb{R}^2}} \\ &= \max_{u \neq 0}\frac{\|Au\|_{\mathbb{R}^2}}{\|u\|_{\mathbb{R}^2}} \\&= 2\end{aligned}\]
と求められました。
積分作用素
\[F_1 (u) = \int_0^1 u(x)dx\]
の作用素ノルムを求めます。
さきほど、すべての\(u \in L^1\)に対し、\(|F_1(u)| \leq \|u\|_{L^1}\)であることを示しました。
また、\(u(x) \equiv 1\)という定数関数を考えると、\(u \neq 0\)で、
\[\|u\|_{L^1}=\int_0^1 |1| dx =1\]
なので、
\[\begin{aligned} & \|F_1\|_{B(L^1,\mathbb{R})}\\ &= \sup_{u \neq 0} \frac{|F_1(u)|}{\|u\|_{L^1}} \\ &= \max_{u \neq 0} \frac{|F_1(u)|}{\|u\|_{L^1}} \\&= 1\end{aligned}\]
と求められます。
微分作用素
微分作用素
\[F_2 (u) = \frac{du}{dx}\]
について、\(C^0,C^0\)ノルムのときは、どんな実数\(M\)に対しても、\(\|F_2(u)\|_{C^0}> M\|u\|_{C^0}\)を満たす\(u \neq 0\)が存在することを示しました。
つまり、\(\{ \frac{\|F_2(u)\|_{C^0}}{\|u\|_{C^0}} \mid u \neq 0\}\)は、上に有界ではありません。上界\(K\)があったとすると、それより大きな\(M\)を考えて逆向きの不等式\(\frac{\|F_2(u)\|_{C^0}}{\|u\|_{C^0}} >M>K\)が成り立つので、\(K\)が上界であることに矛盾します。
よって、上限は存在せず、\(\|F_2\|_{B(C^1,C^0)}= \sup_{u \neq 0} \frac{\|F_2(u)\|_{C^0}}{\|u\|_{C^0}} = \infty\)となります。
非有界な作用素に対しては、「作用素ノルム」はノルムとならない、関数として有限の値を持たないわけですね。
以上、有界線形作用素、ノルムとは:行列、積分作用素、微分作用素の例を紹介してきました。
関連して知っておきたい話、この記事では議論を省略したこととして、
- 線形作用素について、有界性と連続性は同値
- 作用素ノルムの複数の定義の同値性
- 行列の作用素ノルム
- 有界線形作用素のなす集合\(B(X,Y)\)が作用素ノルムについてノルム空間となること
- 重要な有界線形作用素のクラスとして、コンパクト作用素があること(コンパクトならば有界)
があります。これらについては別記事で紹介予定です。
作用素ノルムの計算はやや面倒ですが、有界であることを示すまでなら比較的簡単です。行き先の大きさ\(\|F(u)\|\)を見て予想を立てつつ、線形作用素が有界か非有界か判定できるようになると良いですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)
こちらもおすすめ
行列全体のなす集合が線形空間(ベクトル空間)となることの証明
上限・下限(sup,inf)、有界とは:具体例、最大・最小値との違い