上限・下限（sup,inf）、有界とは：具体例、最大・最小値との違い

どうも、木村（@kimu3_slime）です。

微積分学の基礎で扱う、上限や下限、有界という考え方の具体例、最大・最小値との違いを紹介します。

上限・下限をなぜ考えるか
上限・下限の定義と求め方
こちらもおすすめ

上限・下限をなぜ考えるか

僕は初めて上限や下限の考え方に教科書や講義で出会ったときに、正直なところ何を言っているかわけがわかりませんでした。

そこで今回は、高校の数学からでも学べるような簡単な話をしたいと思います。

高校数学では、関数の最大値や最小値を求める問題をよく考えました。

そのとき、\(x\)の動きうる範囲（定義域）に制限があることが多かったはずです。例えば、\(0 \leq x \leq 5\)のときに、\(f(x)=x^3-x\)の最大値と最小値を求めよ、といったように。関数の最大値や最小値を

\[ \begin{aligned}\max _{x \in [0,5]} f(x)=120\end{aligned} \]

\[ \begin{aligned}\min _{x \in [0,5]} f(x)=-\frac{2}{3\sqrt{3}}\end{aligned} \]

といったように表します。\(\max\)は最大値（maximum）、\(\min\)は最小値（minimum）を略した記号です。

定義域によって関数の最大値・最小値の状況は変わってきます。連続な関数は、有界な閉区間\([a,b]=\{x \in \mathbb{R} \mid a \leq x \leq b\}\)上ならば必ず最大値・最小値を持つことが知られています。

参考：コンパクト性とは：有界閉集合、最大値の定理を例に

大学数学では、定義域が実数全体\(\mathbb{R}\)であったり、非有界な区間\([a,\infty) := \{ x \in \mathbb{R} \mid a \leq x\}\)、有界であっても閉区間でない区間\((a,b) =\{ x \mid a<x<b\}\)を考えます。

集合の記法に慣れていないならば：集合論入門：集合の定義、数の集合、ラッセルのパラドックス

\(f(x)= \frac{1}{x}\)という関数を、正の実数全体\((0,\infty)=\{x \mid x>0\}\)で定義されたものとして考えましょう。

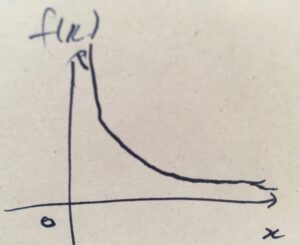
この関数の最大値・最小値はなんでしょうか？　考えても、存在しそうにありませんね。\(0\)に近い値を考えればいくらでも大きくなりますし、\(x\)を大きくすれば限りなく\(0\)に近い値を取るものの、決して\(0\)にはなりません。

極限では\(\lim _{x \to \infty}\frac{1}{x}=0\)ですが、それは有限の値\(x\)で実際に\(f(x)=0\)となることを意味していません。

それでも、関数に対していつでも最大値や最小値のようなものを考えたい。そこで登場するのが上限や下限の考え方です。理屈は後で説明しますが、この状況を

\[ \begin{aligned}\sup_{x\in (0,\infty)} \frac{1}{x}= \infty\end{aligned} \]

\[ \begin{aligned}\inf_{x\in (0,\infty)} \frac{1}{x}= 0\end{aligned} \]

と表現します。読み方としては、関数\(\frac{1}{x}\)の区間\((0,\infty)\)における上限は存在しない（無限大である）、\(\frac{1}{x}\)の区間\((0,\infty)\)における下限は0である、といったものです。

\(\sup\)は上限（supremum）、\(\inf\)は下限（infimum）を略した記号です。日本では、スープ、インフと発音されることが多いでしょう。

冒頭で考えた関数では、最大値と最小値が存在しました。そのときは、最大値と上限、最小値と下限は一致します。

\[ \begin{aligned}\max _{x \in [0,5]} f(x)=\sup _{x \in [0,5]} f(x)\end{aligned} \]

\[ \begin{aligned}\min _{x \in [0,5]} f(x)=\inf _{x \in [0,5]} f(x)\end{aligned} \]

という関係が成り立ちます。このように、上限・下限の考え方は、最大値や最小値が存在しないケースでも、それに近い数を捉えるために使えます。

有界な連続関数のなす集合\(B(U)\)では、

\[ \begin{aligned}\|f(x)\| := \sup _{x \in U} f(x)\end{aligned} \]

というノルムを考えることができます。これは上限ノルムと呼ばれ、広く応用に登場するものです。ノルムは関数列の極限について考えるときに重要で、これを後々に考えるために上限や下限の考え方を学ぶ、と言っても良いのではないでしょうか。

参考：距離空間とは：関数空間、ノルム、内積を例に

上限・下限の定義と求め方

では、上限や下限が

\[ \begin{aligned}\sup_{x\in (0,\infty)} \frac{1}{x}= \infty\end{aligned} \]

\[ \begin{aligned}\inf_{x\in (0,\infty)} \frac{1}{x}= 0\end{aligned} \]

となることは、どうやって考えたら良いのでしょうか。

まず関数の上限・下限とは、関数の取りうる値の集合（像）の上限・下限として定義されます。

\[ \begin{aligned}\sup _{x\in U}f(x) := \sup f(U)\end{aligned} \]

\[ \begin{aligned}\inf _{x\in U}f(x):= \inf f(U)\end{aligned} \]

今回の例ならば、0より大きなすべての値を取り、\(f((0,\infty)):=\{\frac{1}{x} \mid x \in (0,\infty)\} = (0,\infty)\)となります。

参考：線形写像の核、像の定義：部分空間となることの証明

そのため、教科書では実数の部分集合\(A\)に対して、上限や下限を定義するでしょう。

\[ \begin{aligned}\sup (0,\infty)= \infty\end{aligned} \]

\[ \begin{aligned}\inf (0,\infty) = 0\end{aligned} \]

となります。

上限や下限を判定する第一段階として、上に有界、下に有界という考え方があります。

\(A \subset \mathbb{R}\)が上に有界（bounded from above）であるとは、実数\(K\)ですべての\(x\in A\)に対し\(x \leq K\)を満たすものが存在することです。下に有界（bounded from below）とは、実数\(K\)ですべての\(x\in A\)に対し\(K \leq x\)を満たすものが存在することです。

有界であるとは（bounded）、ある一定の数によって集合\(A\)の取りうる値が制限されているイメージです。

\((0,\infty)\)は、上に有界ではありません。すべての\(x\in (0,\infty)\)に対し\(x \leq K\)を成り立たせるような数は存在しないからです。上に有界の否定：任意の\(K \in \mathbb{R}\)に対し、\(K+1 \in (0,\infty)\)であり、\(K +1 > K\)が成り立つので。

参考：「すべての」「存在する」「一意性」とは？証明の書き方

\((0,\infty)\)は、下に有界です。例えば\(K=-1\)としましょう。すると、すべての\(x\in (0,\infty)\)に対し、\(0<x\)より\(-1 \leq x\)が成り立つので。

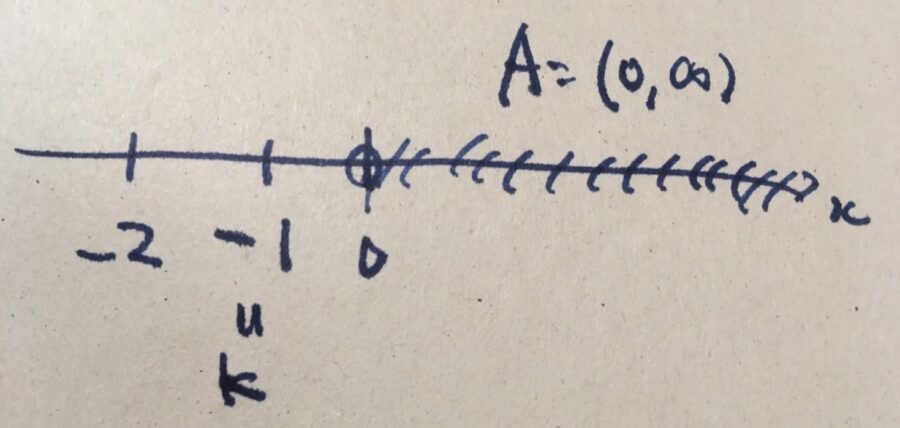
上に有界、かつ下に有界な部分集合を、有界な集合（bounded set）と呼び、そうでないものを非有界な集合（unbounded set）と呼びます。\((0,\infty)\)は上に有界でないので、非有界な集合です。

\((0,\infty)\)は下に有界なので、まずはそちらの方面を考えていきましょう。そこから\(0\)という値を取り出すにはどう定義したら良いでしょうか。

下に有界であることを示す定義で、\(K\)としてはさまざまなものが選べます。\(K=-1,-1000,0\)としても、すべての\(x\in (0,\infty)\)に対して\(K \leq x\)は成り立ちますね。この性質を満たす\(K\)を、集合\(A\)の下界（lower bound）と呼びます。下側で抑えられる数はたくさんあって、それらすべてを下界と呼ぶわけです。

下界の中で最も\(A\)に近い要素は何かと考えてみます。それは\(K=0\)です。これは下界の中で最大のもの（greatest lower bound）になっており、最大の下界を下限と呼び、\(\inf (0,\infty)=0\)と定義しましょう。条件をまとめると、次のようになります。

実数\(K\)が集合\(A\)の下限である\(\inf A =K\)とは、

下界である：すべての\(x \in A\)に対し、\(K \leq x\)
下界の中で最大である：すべての\(L >K\)に対し、\(x < L\)となる\(x\in A\)が存在する

と定義します。

\(\inf (0,\infty)=0\)であることを示しましょう。\(0\)が\((0,\infty)\)の下界であることは既に確かめました。残りは、\(0\)より真に大きな数\(L>0\)が\(A\)の下界でないことを確かめれば良いです。\(L>0\)とすると、例えば\(\frac{L}{2} \in (0,\infty)\)であり、\(\frac{L}{2} <L\)を満たします。よって、\(0\)が下限であると言えました。

\(K\)が\(A\)の下限であり、かつ\(K \in A\)でもあるとき、\(K\)を\(A\)の最小値と呼びます \(\min A = K\)。

\((0,\infty)\)の下限は0ですが、\(0 \not \in (0,\infty)\)なので、\(0\)は最小値ではありません（最小値を持たない）。\([0,\infty]=\{x \mid x \geq 0\}\)と\(0\)を含むような集合を考えれば、\(\inf [0,\infty]=\min [0,\infty]=0\)であることが示せます（定義によって確かめてみてください）。

上限も、下限と同様に考えます。つまり、最小の上界（upper bound）を上限と呼ぶわけです。

実数\(K\)が集合\(A\)の上限である\(\sup A =K\)とは、

上界である：すべての\(x \in A\)に対し、\(x \leq K\)
上界の中で最小である：すべての\(L <K\)に対し、\(x > L\)となる\(x\in A\)が存在する

と定義します。

どんな実数\(K\)も、\((0,\infty)\)の上限ではありません。既に確かめたように、\((0,\infty)\)は上に有界ではないのです。上限の定義を満たす実数が存在しないとき、\(A\)の上限は存在しないと言い、形式的な記号ですが\(\sup A= \infty\)と書きます。つまり、\(\sup (0,\infty )= \infty\)が成り立ちます。

同様に、下に有界でない集合には下限が存在しません。このとき、\(\inf A = -\infty\)と書きます。例えば、\(\inf (-\infty ,1]= -\infty\)です。

実数の基本的な性質（実数の公理）として