どうも、木村(@kimu3_slime)です。
今回は、微積分学における部分列、ボルツァーノ・ワイエルシュトラスとは何か、点列コンパクトとの関係を紹介します。
部分列、ボルツァーノ・ワイエルシュトラスの定理
さっそくですが、注目したい定理を述べましょう。
ボルツァーノ・ワイエルシュトラスの定理(Bolzano–Weierstrass theorem)
すべての実数列は有界ならば、収束する部分列を持つ。
この主張は何を言っているのか、順を追って話したいと思います。
まず、収束する数列は必ず有界な数列となる、という一般論があります。収束の定義から、ある番号\(N\)以降はその変動は例えば1以下であるようにできます。また、それ以前の項は有限個なので、その変動の最大値を利用すれば良いわけです。
つまり、収束する数列を見つけたかったら、必ず有界な数列の中から見つけなければなりません。もし非有界な数列を考えたら、それは収束しないので。
では、有界な数列を考えれば必ず収束するかというと、そういうわけでもありません。
例えば、\(a_n =(-1)^n\)という数列を考えましょう。\(K=1\)とすると、すべての\(n\in \mathbb{N}\)に対し、\(|a_n| =1 \leq K\)となるので、これは有界な数列です。
しかしこの数列は収束しません。どんな極限値\(a\)を想定したとしても、番号\(n\)をひとつずらしただけで値が\(1,-1\)と変動してしまうので、例えば変動幅\(\varepsilon =1\)に対応できません。
収束せず、正負も無限大にも発散しないこのような数列は、振動する数列と呼ばれるものです。
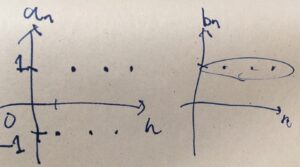
それでも、この数列の項を取り出して収束するような数列を作り出すことができます。具体的には、例えば\(b_n := a_{2n}\)や\(c_n := a_{2n+1}\)とすれば良いわけです。そうすれば、\(b_n\)は\(1\)に、\(c_n\)は\(-1\)に収束します。
ボルツァーノ・ワイエルシュトラスの定理は、この例の数列に限らず、有界な数列はすべて、収束するような部分列を取り出すこができる、という主張です。
上の例では、\(b_n =a_{2n}\)や\(c_n = a_{2n+1}\)と\(2n,2n+1\)番目の項を取り出す操作をしました。これを一般化した考え方が、部分列です。
\((a_n)_{n \in \mathbb{N}}\)を数列とします。項を取り出すことは、狭義の単調増加な関数\(f:\mathbb{N}\to \mathbb{N}\)を考えることと言えます。これによって定まる数列\(b_n := a_{f(n)}\)を、\((a_n)\)の部分列(subsequence)と呼びましょう。その関数を点列\((k_n)\)と表すことで、部分列を\(a_{k(n)}\)や\(a_{k_n}\)と書くこともあります。
\(f\)が狭義単調増加であるとは、すべての\(n\)に対して\(f(n+1)> f(n)\)が成り立つことです。\(f(n)=2n\)や\(g(n)=2n+1\)はこの条件を満たすので、\((b_n),(c_n)\)は部分列の条件を満たしているわけですね。
狭義単調増加という条件を課すことは、同じ番号の項を2度使わない、項の順番を前後に入れ替えてはいけない、ということです。例えば同じ番号の項を何度でも使って良いとなったら、必ず収束する数列が取り出せることがわかりますね(笑)。
ボルツァーノ・ワイエルシュトラスの定理によって、収束する部分列を持つと何が嬉しいのでしょうか。
例えば、ある条件を満たす数列が、有界であることを示せれば、そこから部分列を取ってその数列の極限の存在が言えます。つまり、期待する条件(例えば方程式)を満たす数の存在を示すために使えるものです。
参考:非負行列・正行列のペロン・フロベニウスの定理とは、証明
ボルツァーノ・ワイエルシュトラスの定理は、「定理」とは呼びますが、他の実数の公理と同値です。例えば、
単調収束定理(monotone convergence theorem)
上に有界な単調増加な数列は、収束する。
下に有界な単調減少な数列は、収束する。
との関連はわかりやすいでしょう。
ボルツァーノ・ワイエルシュトラスの定理の証明は、おおざっぱ言えば次のようなものです。有界な数列なので、その数列の取りうる範囲を、二分法的に狭めていくことができます。部分列を選べば、取りうる範囲の区間をどんどん小さくしていくことができ、区間縮小法(はさみうちの原理)より極限の存在が言えます。実数の公理との同値性について詳しくは、杉浦「解析入門 Ⅰ」を参照してください。
点列コンパクトとの関係
ボルツァーノ・ワイエルシュトラスの定理は、多次元\(\mathbb{R}^N\)の実数列(点列)についても同様に成り立ちます。
そして、「収束する部分列を持つ」という性質は、実数に限らず位相空間の用語で一般化されます。
位相空間の部分集合\(A\)が点列コンパクト(sequentially compact )であるとは、\(A\)上の点列\((a_n)_{n \in \mathbb{N}}\)が\(A\)において収束する部分列を持つことです。
この言葉で定理を言い換えると、「\(\mathbb{R}^N\)の有界な閉集合は、点列コンパクトである」となります。
これと似た概念と主張に、コンパクト性、ハイネ・ボレルの被覆定理がありました。
ハイネ・ボレルの被覆定理(Heine–Borel theorem)
\(D \subset \mathbb{R}^N\)とする。\(D\)がコンパクトであることと、\(D\)が有界な閉集合であることは同値。
一般に、距離空間においては、点列コンパクトであることとコンパクトであることは同値になります。
したがって、実数の空間\(\mathbb{R}^N\)においては、ボルツァーノ・ワイエルシュトラスの定理(有界閉集合の点列コンパクト性)とハイネ・ボレルの被覆定理(有界閉集合のコンパクト性)は同値です。これらは等しく、実数の公理として利用できるものと言えます。
実数の基本的な性質は、位相空間論の言葉を使って整理すると、よりクリアに理解できるようになるでしょう。
\(\mathbb{R}^N\)以外の空間を考えると、有界な数列であっても、収束する部分列を持たないことがあります。例えば数列空間におけるそのような列は有名で、それについては関数解析の分野で学ぶことになるでしょう。
以上、部分列、ボルツァーノ・ワイエルシュトラスの定理、点列コンパクト性との関係を紹介してきました。
何らかの方程式の解を見つけるために、それを近似的に構成する数列や点列を作り、そこから収束する部分列を取り出す、ということを解析学ではよく考えます。その基礎的な議論として、実数のケース、有界な数列から収束する部分列が取り出せる、という性質はぜひ知っておくと良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
共立出版 (1984-12-21T00:00:01Z)
¥682 (中古品)
岩波書店 (1978-03-23T00:00:01Z)
¥5,060
岩波書店 (1981-11-15T00:00:01Z)
¥5,720
東京大学出版会 (1980-03-31T00:00:01Z)
¥3,080
東京大学出版会 (1985-04-25T00:00:01Z)
¥1,884 (中古品)
こちらもおすすめ
上限・下限(sup,inf)、有界とは:具体例、最大・最小値との違い
なぜe(オイラー数)を学ぶ? 指数関数、対数関数の微分を単純化