数列の上極限・下極限（limsup,liminf）の例、性質

どうも、木村（@kimu3_slime）です。

今回は、数列の上極限・下極限（limsup,liminf）とは何か、例と求め方、性質を紹介します。

上極限・下極限の定義と例
上極限・下極限の性質
こちらもおすすめ

上極限・下極限の定義と例

上極限や下極限という考え方は、通常の極限を拡張したような性質を持っています。

早速ですが、実数列\((a_n)_{n \in \mathbb{N}}\)に対して、次のように定義をします。

\[ \begin{aligned}\limsup_{n\to \infty} a_n := \inf_{k \in \mathbb{N}} \sup_{n \in \mathbb{N}, n \geq k} a_n\end{aligned} \]

\[ \begin{aligned}\liminf_{n\to \infty} a_n := \sup_{k \in \mathbb{N}} \inf_{n\in \mathbb{N}, n \geq k} a_n\end{aligned} \]

を数列\((a_n)\)の上極限（じょうきょくげん limit superior）、下極限（かきょくげん limit inferior）と呼びます。

記号としては、リミットスープ、リミットインフと読むことが多いでしょうか。上極限、下極限は\(\limsup = \varlimsup\)、\(\liminf=\varliminf\)と横棒（バー）を使って書くこともあります。

なんだかいかめしい定義に見えますが、簡単な例で少しずつ考えていけばイメージはつかめるでしょう。

ただし、まずは上限・下限とは何かを知っておく必要はありますが。

\(a_n= \frac{1}{n}\)の上極限、下極限を求めてみたいと思います。

上極限を求めることは、2段階の仕組みになっています。まず上限を取って、続いて下限を取る、といったように。

\(k\)を任意の自然数として、\(\sup _{n \in \mathbb{N} ,n \geq k }a_n\)を求めましょう。\(a_{n}=\frac{1}{n}\)は単調減少であり、\( k \geq n\)において値が最も大きくなるのは\( n =k\)のときで、以降は\(\frac{1}{n} =a_n \leq \frac{1}{k}\)となっています。つまり、\(\sup _{n \in \mathbb{N} ,n \geq k } a_n= \frac{1}{k}\)です。そして、\(\frac{1}{k}\)の\(k\)に関する下限を求めれば、\(\inf_{k \in \mathbb{N}} \frac{1}{k}=0\)。よって、

\[ \begin{aligned} \limsup_{n \to \infty }\frac{1}{n}&=\inf_{k \in \mathbb{N}} \sup_{n \in \mathbb{N}, n \geq k} \frac{1}{n}\\&= \inf_{k \in \mathbb{N}} \frac{1}{k} \\ &= 0\end{aligned} \]

と求められました。

下極限についても同様です。\(k\)を任意の自然数として、\( n \geq k\)を満たす任意の自然数\(n\)に対して、\(a_n =\frac{1}{n} \geq 0\)なので、\(0\)はその下界です。\(a_n\)は\(0\)より真に小さい値を取らないので、\(0\)は下限でもあり、\(\inf_{n\in \mathbb{N},n \geq k} a_n=0\)。よって、

\[ \begin{aligned} \liminf_{n \to \infty }\frac{1}{n}&=\sup_{k \in \mathbb{N}} \inf_{n \in \mathbb{N}, n \geq k} \frac{1}{n}\\&= \sup_{k \in \mathbb{N}} 0 \\ &= 0\end{aligned} \]

となります。

この例では、\(\lim_{n\to \infty }a_n = \limsup_{n\to \infty} a_n = \liminf_{n\to \infty}a_n\)が成り立っていますね。一般に、収束する数列に対しては、上極限と下極限が一致します。

初めて「上極限・下極限を求めよ」という問題を見たとき、下限や上限がごちゃごちゃになって、何をしていいかわからなくなってしまうかもしれません。上極限ならば

\(k\)を固定して、大きな番号に対する上限\(\sup_{n \in \mathbb{N}, n \geq k} a_n\)を求める
求めた上限の下限を取る

と問題を2つに分ければ、上限・下限を求める問題となります。そもそも上限・下限の求め方がわからない場合は、そこまで勉強を戻る必要があるでしょう。

収束する数列を考える上では、上極限・下極限のありがたみを感じにくいでしょう。次のような例を捉えるのに、上極限・下極限は役立ちます。

\(a_n =(-1)^n\)の上極限・下極限を求めてみましょう。これは振動する数列で、普通の極限は持ちません。

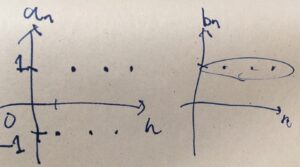
まず上極限を求めます。\(k\)を任意の自然数としましょう。\(n \geq k\)のとき\(a_n \leq 1\)であり（\(1\)は上界）、\(1\)より真に大きな値は取りません。よって、\(\sup_{n \in \mathbb{N}, n \geq k}=1\)です。これは\(k\)に依存しないので、\(\limsup _{n\to \infty}(-1)^n =1\)となりました。「上側の極限値」とでもいった数値が取り出せています。

下極限を求めましょう。同様にして、\(\inf_{n \in \mathbb{N}, n \geq k}=-1\)です。よって、\(\liminf _{n \to \infty}(-1)^n = -1\)となりました。「一番小さくなりうる極限値」のようなものが取り出せています。

似たような例ですが、もうひとつやってみます。

\[ \begin{aligned}a_n= \begin{cases}\frac{1}{n}+1 & n が奇数のとき \\ -\frac{1}{n}-1 & n が偶数のとき\end{cases}\end{aligned} \]

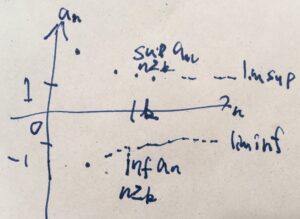
この数列は\(n\)が1つ増えるごとに符号を変えて振動していますが、部分的に見ると「極限」が見つかりそうです。つまり、奇数項を見れば\(1\)に、偶数項を見れば\(-1\)に近づいていきそうです。それを取り出せるのが、上極限や下極限と言えます。

任意に自然数\(k\)を選びましょう。\(k\)番目以降の上限と下限を求めると、部分的には単調減少・単調増加で、

\[ \begin{aligned}\sup_{n \in \mathbb{N}, n \geq k} a_n = \begin{cases}\frac{1}{k}+1 & k が奇数のとき \\ \frac{1}{k+1}+1 & k が偶数のとき\end{cases}\end{aligned} \]

\[ \begin{aligned}\inf_{n \in \mathbb{N}, n \geq k }a_n = \begin{cases}-\frac{1}{k+1}-1 & k が奇数のとき \\ -\frac{1}{k}-1 & k が偶数のとき\end{cases}\end{aligned} \]

となります。よって、それぞれで\(k\)に関する下限、上限を取れば、\(\limsup_{n\to \infty}a_n=1\)、\(\liminf_{n\to \infty}a_n=-1\)がわかりました。

上極限・下極限の性質

上極限・下極限に関する性質で、重要なものを紹介しましょう。それは

次の条件は同値である。

\(a_n\)が収束する（\(\lim_{n\to \infty}a_n\)が存在する）
上極限と下極限が一致する \(\liminf_{n\to \infty}a_n = \limsup_{n \to \infty}a_n\)

この性質は、\(a_n\)が正の無限大（負の無限大）に発散するケースでも同様に成り立つ。

つまり、数列の収束を判定するときに、それを上極限と下極限を求めるという別々の問題にバラせるわけです。一般に、数列の極限値ピッタリを求めることは難しいですが、上極限や下極限なら不等式評価によって求められたりします。

この事実を支えているのは、

\((b_n)\)を\((a_n)\)の任意の収束する部分列とする。このとき、\[ \begin{aligned}\limsup a_n \leq \lim_{n\to \infty} b_n \leq \limsup a_n\end{aligned} \]である。つまり、上極限は部分列の極限のうち最大で、下極限は部分列の極限のうち最小。
\(a_n\)の上限、下限に収束する部分列は常に存在する（単調収束定理とボルツァーノ・ワイエルシュトラスの定理）

ことです。

他にも、

上極限が\(a = \limsup a_n\)であることは、次のことと同値。
- 任意の\(\varepsilon>0\)に対し、\(a+\varepsilon<a_n \)となる\(n\)は有限個
- 任意の\(\varepsilon>0\)に対し、\(a-\varepsilon>a_n \)となる\(n\)は無限個
下極限についても同様。

といった性質は基本的です。

証明について、詳しくは杉浦「解析入門 Ⅰ」を参照してください。

上極限や下極限の考え方は、たとえば級数の収束判定で利用されます。

コーシーの判定法、コーシー・アダマールの公式

\(\limsup |a_n|^{\frac{1}{n}}\)が1以下なら級数\(\sum a_n\)は収束、1以上なら発散する。

\(\limsup |a_n|^{\frac{1}{n}}=\frac{1}{R}\)とすると、\(R\)はべき級数\(\sum a_n z^n\)の収束半径である。

参考：べき級数の収束半径とは何か、テイラー展開を例にした求め方、複素べき級数、収束半径とは：指数・三角関数を例に

また、積分と極限の順序交換の定理、ルベーグ積分における収束定理を支える補題にも登場します。

ファトウの補題

\((f_n)\)を（可測）関数列とする。\(g\)を可積分な非負値関数とする。関数列の下限が\(-g\)で抑えられているならば

\[ \begin{aligned}\int \liminf f_n d\mu \leq \liminf \int f_n d \mu\end{aligned} \]

上限が\(g\)で抑えられているならば