どうも、木村(@kimu3_slime)です。
今回は、べき級数の収束半径とは何か、その求め方を、初等関数のテイラー展開を例として交えつつ紹介します。
べき級数とは何か
微分できる関数を多項式\(a_n x^n\)の和(級数)として表す方法は、テイラー展開と呼ばれるのでした。例えば、指数関数は
\[ \begin{aligned}e^x = 1+ x + \frac{x^2}{2!}+\cdots = \sum_{k=0} ^\infty \frac{1}{k!}x^k\end{aligned} \]
と展開されます。
一般に、右辺に登場するような\(x^k\)の無限級数
\[ \begin{aligned} \sum_{k=0} ^\infty a_k x^k =a_0 +a_1 x+ a_2 x^2 +\cdots\end{aligned} \]
を、べき級数(power series)と呼びます。係数\(a_k\)は無限にあるわけですが、それはひとつの数列\(\{a_k\}_{k=0} ^\infty\)で表せるものです。
指数関数のテイラー展開では、係数が\(a_k =\frac{1}{k!}\)となっています。
収束半径とは何か
一旦、既知の関数のテイラー展開から離れ、一般の数列\(\{a_k\}_{k=0} ^\infty\)により定まるべき級数\( \sum_{k=0} ^\infty a_k x^k\)を考えてみましょう。
べき級数は、いつでも収束するとは限りません。数列\(\{a_k\}_{k=0} ^\infty\)や変数\(x\)の値によって、級数が収束するかどうかは変わってきます。
例えば、常に\(a_k=1\)として、\( \sum_{k=0} ^\infty x^k\)という級数の収束を判定してみます。
高校数学を思い出せば、それは初項\(x^{0}=1\)、公比\(x\)の等比数列により定まる無限級数です。その有限部分和は、
\[ \begin{aligned}1+x+\cdots + x^{\ell}=\frac{1-x^\ell}{1-x}\end{aligned} \]
なので、\(\ell \to \infty\)での収束は\(x^\ell\)の項に依存しています。
もし\(-1<x<1 \)ならば、\(x^\ell \to 0\)なので収束して、
\[ \begin{aligned}\lim _{\ell \to \infty} \sum_{k=0} ^\ell x^k =\frac{1}{1-x}\end{aligned} \]
となります。
一方で、\(x<-1 \)または\(x>1\)ならば、\(x^{\ell}\)はどんどん大きくなり、収束しません。
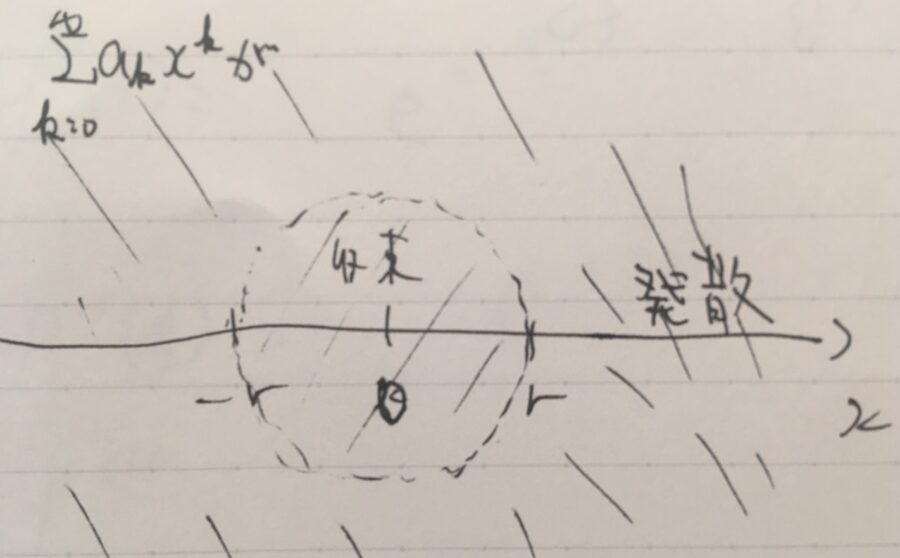
この級数の収束は、\(r:=1\)を境に変化しています。つまり、\(|x|<r\)ならば収束し、\(|x|>r\)ならば発散しているといったように。
この議論を一般化して、収束半径という考え方を導入しましょう。\(r>0\)として、べき級数
\[ \begin{aligned} \sum_{k=0} ^\infty a_k x^k\end{aligned} \]
が、\(|x|<r\)ならば収束し、\(|x|>r\)ならば発散するとき、\(r\)をべき級数の収束半径(radius of convergence)と呼びます。すべての\(x\)について収束するときは、収束半径は無限大\(r=\infty\)と約束しましょう。
先ほどの議論により、常に\(a_k=1\)のときは、収束半径は\(r=1\)です。
\(-r<x<r\)という区間の内側なら収束、外側\(x<-r,r<x\)なら発散するという意味では、収束半径は収束区間の大きさを表す数字、と言っても良いでしょう。
(あえて半径と呼ぶのは、実変数\(x\)を複素変数\(z\)に置き換えた、複素べき級数の議論でも収束半径が考えられるからです。複素平面において、円内ならば収束、円外ならば発散となるような半径が考えられます。(別記事で紹介するかも)
(収束半径の定義では、境界上の点\(x= r,-r\)における収束は問うていません。個別の級数によって、収束したりしなかったりします。しかし大部分の\(x\)について、\(r\)を境に収束と発散が分かれるので、その境を収束半径と呼ぶわけです。)
収束半径の求め方(レシオテスト)
一定の条件を満たしていれば、収束半径を求める一般的な方法があります。
そのひとつがレシオテスト(ratio test)、ダランベールの収束判定法と呼ばれる方法です。レシオ、すなわち隣り合った項の比\(| \frac{a_{k+1}}{a_k }|\)に注目した判定方法と言えます。
\(\{a_k\}_{k=0} ^\infty\)により定まるべき級数\( \sum_{k=0} ^\infty a_k x^k\)を考える。係数の比の極限\(\lim_{k\to \infty}| \frac{a_{k+1}}{a_k }|\)が存在すると仮定する。
このとき、
\(|x|<\frac{1}{\lim_{k\to \infty}| \frac{a_{k+1}}{a_k}| }\)ならば級数は収束し、
\(|x|>\frac{1}{\lim_{k\to \infty}| \frac{a_{k+1}}{a_k}| }\)ならば級数は発散する。
すなわち、\(r:= \frac{1}{\lim_{k\to \infty}| \frac{a_{k+1}}{a_k}| }\)はべき級数の収束半径である。
まずは一般論抜きにして、具体的に考えてみましょう。
指数関数のテイラー展開を例として、収束半径を求めてみます。
\[ \begin{aligned}e^x =\sum_{ k=0} ^\infty\frac{1}{k!} x^k\end{aligned} \]
これを等比数列の和として見たいですが、係数がかかっているため等比とは言えません。そこで、この級数より大きな収束する等比数列で抑え込めないか、と考えます。
べき級数の拡大比率、\(k\)項目と\(k+1\)項目の比の大きさに注目してみます。
\[ \begin{aligned}|\frac{\frac{1}{(k+1)!} x^{k+1}}{\frac{1}{k!} x^k}|=|\frac{k!}{(k+1)!}x|=|\frac{x}{k}|\end{aligned} \]
\(k\)が十分大きいとき、右辺は\(x\)に依存せずにいくらでも小さくできます。例えば、\(k\)がある一定の自然数\(K\)より大きいとき\(k \geq K\)に、
\[ \begin{aligned}|\frac{\frac{1}{(k+1)!} x^{k+1}}{\frac{1}{k!} x^k} |\leq \frac{1}{2}\end{aligned} \]
とできます。この評価を繰り返し用いれば、
\[ \begin{aligned}|\frac{1}{(k+2)!} x^{k+2} |\leq |\frac{1}{2}{\frac{1}{(k+1)!} x^{k+1}}| \leq |\frac{1}{2^2} \frac{1}{k!} x^{k}|\end{aligned} \]
といったような評価ができます。よって、十分先の項が等比級数によっておさえられることがわかるのです。
\[ \begin{aligned} \sum_{ \ell=0} ^k |\frac{1}{\ell !} x^\ell| & \leq\sum_{ \ell=0} ^{K-1} |\frac{1}{\ell !} x^\ell| + |\frac{1}{K!} x^K| + |\frac{1}{(K+1)!} x^{K+1}|+\cdots +|\frac{1}{k!} x^k|\\ & \leq \sum_{ \ell=0} ^{K-1} |\frac{1}{\ell !} x^\ell| + |\frac{1}{K!} x^K| + |\frac{1}{2}\frac{1}{K!} x^K|+\cdots +|\frac{1}{2^{k-K}}\frac{1}{K!} x^K| \\ &= \sum_{ \ell=0} ^{K-1} |\frac{1}{\ell !} x^\ell| + |\frac{1}{K!} x^K| (1 + \frac{1}{2}\cdots +\frac{1}{2^{k-K}} )\end{aligned} \]
となりますが、\((1 + \frac{1}{2}\cdots +\frac{1}{2^{k-K}} )\)は公比\(\frac{1}{2}\)の等比級数なので、\(k\to \infty\)で収束します。また、それ以外の項は\(k\)に依存しない定数で、全体としても収束しています。
よって、
\[ \begin{aligned}|\sum_{ k=0} ^\infty\frac{1}{k!} x^k| \leq \sum_{ k=0} ^\infty|\frac{1}{k!} x^k| <\infty\end{aligned} \]
と、指数関数のテイラー展開は、どのような\(x\)についても収束することがわかりました。収束半径は\(r=\infty \)です。
収束半径が限りなく大きく取れた理由は、どのような\(x\)に対しても、\(k\)を大きくすることで、項の比の大きさが限りなく小さくできることにあります。
\[ \begin{aligned}\lim_{k\to \infty} |\frac{\frac{1}{(k+1)!} x^{k+1}}{\frac{1}{k!} x^k}|=|\frac{k!}{(k+1)!}x|= \lim_{k\to \infty}|\frac{x}{k}|=0\end{aligned} \]
三角関数のテイラー展開についても、指数関数と同様の評価で、収束半径が\(r= \infty\)であることが示せます。
一方で、対数関数のテイラー展開では様子が変わってきます。
\[ \begin{aligned}\log(1+x) = \sum_{k=1}^{\infty}\frac{(-1)^{k-1}}{k} x^k \end{aligned} \]
再び、隣り合った項の比を調べてみると、
\[ \begin{aligned}|\frac{\frac{(-1)^{k}}{k+1} x^{k+1}}{\frac{(-1)^{k-1}}{k} x^k}|=|\frac{k}{k+1} x|=|\frac{1}{1+\frac{1}{k}} x|\end{aligned} \]
であり、\(k\to \infty\)では
\[ \begin{aligned}\lim_{k\to \infty} | \frac{\frac{(-1)^{k}}{k+1} x^{k+1}}{\frac{(-1)^{k-1}}{k} x^k}|=| x|\end{aligned} \]
と収束するものの、大きさが\(x\)に依存しています。
\(|x|<1\)のときは、さきほどの議論と同様に、1以下の公比を持つ等比級数で上から抑えることができ、収束します。
一方で、\(|x|>1\)のときは、1以上の公比を持つ等比級数で下から評価することができ、発散します。
よって、対数関数のテイラー級数の収束半径は、\(r=1\)です。
レシオテストの証明は結局、等比級数との比較によって収束を判定する議論です。この方法は、べき級数に限らない一般の級数に対しても適応できます。
レシオテストは、\(\lim_{k\to \infty}| \frac{a_{k+1}}{a_k }|\)が存在する場合しか有効ではありません。級数の収束判定法としては他に、\(k\)乗根を使ったコーシー・アダマールの判定法、積分と比較するオイラー・マクローリンの判定法などが知られています。
以上、べき級数と収束半径とは何か、テイラー展開を例にした収束半径の求め方(レシオテスト)を紹介してきました。
級数の収束を判定するための方法のひとつが、収束が判定しやすい級数と比較すること、すなわち等比級数と比較することです。そこがわかっていれば、収束半径やその求め方も理解しやすいかと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1978-03-23T00:00:01Z)
¥5,170
東京大学出版会 (1980-03-31T00:00:01Z)
¥3,080



