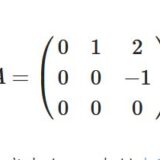どうも、木村(@kimu3_slime)です。
今回は、数列を集めた集合が線形空間となること(数列空間)を証明し、その性質:無限次元、基底、ノルム、バナッハ空間などについて紹介します。
数列空間lとは
\(\ell(\mathbb{N}) :=\{(x_n)_{n\in \mathbb{N}} \mid x_n \in \mathbb{R}\}\)を実数列全体のなす集合としましょう。
例えば、\(x_n =n^2\)とすると、\(1,4,9,16,\dots\)といった数列\((x_n)_{n\in \mathbb{N}}\)が定まります。数列\((x_n)\)は\(\ell(\mathbb{N})\)の要素です。
数列とは何かと言えば、各番号\(n\)に対して、\(x_n\)という数字を対応させる規則のことです。つまり、ひとつの関数\(x: \mathbb{N} \to \mathbb{R}\)と言えます。その集合は、\(\mathrm{Map}(\mathbb{N},\mathbb{R})\)と書くことがあります。
また、\(n\)個の数の組\((x_1,\dots,x_n)\)の集合を\(\mathbb{R}^N\)と書くことに類似させて、数列を無限個の数の組として、\(\mathbb{R}^{\mathbb{N}}\)と表すこともあるでしょう。(厳密に言えば、添字を\(\mathbb{N}\)とする直積集合を考えている)
さて、数列同士を組み合わせ、和やスカラー倍と呼ばれる操作をすることで、新たな数列を生み出すことができます。記述を簡単にするため、ここからは数列の添字の範囲\(\mathbb{N}\)を省略します。
\((x_n),(y_n) \in \ell(\mathbb{N})\)、\(a\in \mathbb{R}\)とします。
\[ \begin{aligned}(x_n)+(y_n) := (x_n+y_n)\end{aligned} \]
\[ \begin{aligned}a(x_n) :=( a x_n)\end{aligned} \]
と数列の和\((x_n)+(y_n)\)、スカラー倍\(a(x_n)\)を定義しましょう。\(x_n+y_n,a x_n\)は実数ですから、和とスカラー倍もまた数列になっています。
集合\(\ell(\mathbb{N})\)と和・スカラー倍は、(抽象)ベクトル空間・線形空間の枠組みを満たすことが示せます。そこで、\(\ell(\mathbb{N})\)を数列空間(sequence space)と呼びます。数列も、一種の「ベクトル」としての性質を持つわけです。確かめましょう。
\(V\)を集合とする。次の条件が、\(V\)は線形空間であることの定義。
\(V\)の任意の要素\(x,y,z\)、任意の数\(a,b\in \mathbb{R}\)に対し、和\(x+y \)、スカラー乗法\(ax \)と呼ばれる\(V\)の要素が定まり、次の条件を満たす。
結合法則:\((x+y)+z = x+(y+z)\)
交換法則:\(x+y =y+x\)
ゼロベクトルの存在:\(\exists o(o+x =x)\)
逆ベクトルの存在:\(\exists w (x+w=o)\)。これを逆ベクトルと言い、\(w=-x\)と書く。
分配法則:\((a+b)x= ax+bx\)
分配法則:\(a(x+y)=ax+ ay\)
両立条件:\((ab)x= a(bx)\)
スカラー乗法の単位要素:\(1x =x\)
すべて、数列の和、スカラー倍の定義に戻って示していきましょう。
数列の結合法則、交換法則、分配法則、両立条件、スカラー乗法の単位要素の条件は、数列の値\(\mathbb{R}\)が持っている性質から導けます。
\[ \begin{aligned} ((x_n)+(y_n))+(z_n) &= (x_n+y_n)+(z_n) \\ &=(x_n+y_n+z_n) \\&= (x_n)+(y_n+z_n) \\ &= (x_n)+((y_n)+(z_n))\end{aligned} \]
\[ \begin{aligned} (x_n)+(y_n)&=(x_n+y_n)\\&= (y_n+x_n)\\ &= (y_n)+(x_n)\end{aligned} \]
\[ \begin{aligned} (a+b)(x_n)&=((a+b)x_n)\\&= (ax_n+bx_n)\\ &= (ax_n)+(bx_n) \\&= a(x_n)+b(x_n)\end{aligned} \]
\[ \begin{aligned} a((x_n)+(y_n))&=a(x_n+y_n)\\&= (a(x_n+y_n))\\ &= (ax_n+ay_n) \\&= (ax_n)+(ay_n) \\&= a(x_n)+a(y_n)\end{aligned} \]
\[ \begin{aligned} (ab)(x_n)&=(ab x_n)\\&= (a(bx_n))\\ &= a(bx_n)\\ &= a(b(x_n))\end{aligned} \]
\[ \begin{aligned} 1(x_n)&=(1x_n)\\&= (x_n)\end{aligned} \]
ゼロベクトルとしては、\(o_n=0\)という恒等的に0になる数列が選べます。任意の\((x_n)\)に対して、\((o_n)+(x_n) =(0+x_n)=(x_n)\)を満たします。
逆ベクトルとしては、\((x_n) \)に対して、\((-x_n) \in V\)が選べます。\((x_n)+(-x_n)=(x_n+(-x_n) )=(0 )=(o_n)\)です。
以上によって、\(\ell(\mathbb{N})\)が線形空間であることが示せました。
数列空間l^pの性質
ここからは、証明は抜きに、数列空間に関する性質を紹介していきましょう。
数列の和(級数)が収束する(有限値を持つ)ような数列を考えると、それもまた線形空間となることが知られています。
\(1 \leq p < \infty\)として、
\[ \begin{aligned}\ell^{p}:=\{(x_n) \in \ell(\mathbb{N}) \mid (\sum_{n=1}^\infty x_n^p)^{\frac{1}{p} }< \infty\}\end{aligned} \]
\[ \begin{aligned}\ell ^{\infty} := \{(x_n) \in \ell(\mathbb{N}) \mid \sup_{n\in \mathbb{N}} |x_n|< \infty\}\end{aligned} \]
と置くと、\(\ell ^{p}\)、\(\ell ^\infty\)は線形空間です。単に数列空間というとき、これらを考えることは多いでしょう。\(\ell ^p\)は\(p\)乗和が収束する数列、\(\ell ^\infty\)は有界な数列のなす空間です。
ユークリッド空間\(\mathbb{R}^N\)では、その\(p=2\)ノルム(ユークリッドノルム)\((\sum _{n=1} ^N x_n ^2 )^\frac{1}{2}\)は、有限値でした。最大値ノルム\( \sup_{n\in \mathbb{N}} |x_n|= \max_{n=1,\dots,N} |x_n|\)も有限です。\(\ell ^p, \ell ^\infty\)は、数列空間にノルムを入れるのに適した舞台となるでしょう。
ノルム、内積、バナッハ、ヒルベルト
\(x\)を\(\ell ^p,\ell ^\infty\)の数列として、
\[ \begin{aligned}\|x\|_{\ell^p}:=(\sum_{n=1}^\infty x_n^p)^{\frac{1}{p} }\end{aligned} \]
\[ \begin{aligned}\|x\|_{\ell^\infty}:= \sup_{n\in \mathbb{N}} |x_n|\end{aligned} \]
と置きましょう。
これはノルムの定義を満たし、\(\ell ^p,\ell ^\infty\)はノルム空間となります。ノルムがあるということは、2つの数列の間の距離が測れることにもつながります。
特に\(p=2\)のときは、内積を考えることができます。
\[ \begin{aligned}\langle x,y\rangle_{\ell^2}:= \sum_{n=1} ^\infty x_n y_n\end{aligned} \]
とすると、これは内積の定義を満たし、\(\ell^2\)は内積空間となります。
これらのノルム、内積は、エルピーノルム、エルツー内積といったように呼ばれます。
さらに、\(\ell^p,\ell ^\infty\)では、距離について完備性を持つこと(コーシー列が収束すること)が示せます。結局は\(\mathbb{R}\)の完備性に帰着させる議論です。
\(\ell^p,\ell ^\infty\)は、完備なノルム空間です。その事実を、バナッハ空間(Banach space)であると呼びます。
また、特に\(\ell ^2\)は、完備な内積空間です。そのことを、ヒルベルト空間(Hilbert space)であると呼びます。
ユークリッド空間\(\mathbb{R}^N\)は完備な内積空間、すなわちヒルベルト空間としての性質を持っています。つまり、\(\ell ^2\)はユークリッド空間と似た良い性質を持った空間というわけです。\(\ell^p,\ell ^\infty\)についても、性質が良いと言えます。
無限次元であること
一方で、\(\mathbb{R}^N\)と\(\ell^p,\ell ^\infty\)には本質的な違いがあります。それは数列空間は有限次元ではない、すなわち無限次元であるということです。
数列空間が有限次元であるとしましょう。次元を\(N\)と表すと、\(N\)個の基底が存在し、\(N+1\)個以上のベクトルは必ず線形従属となります。ここで\(e_i\)を\(i\)項目が\(1\)、その他の項が\(0\)の数列とします。そのノルムは有限和になり、\(\|e_i\|=1\)なので、\(\ell ^p ,\ell ^\infty\)の数列です。
そして、\(e_1,e_2,\dots,e_{N+1}\)は線形独立です。\(N+1\)個の係数\(c_1,\dots,c_{N+1}\)によって、\(c_1e_1 +\cdots +c_{N+1} e_{N+1} =0\)と表されたとしましょう。これは数列としての等式で、右辺はゼロ数列です。左辺の第\(i\)項目を見ると、\(e_i\)以外の項は0となり、\(c_i \)のみが残ります。右辺と比較して、\(c_i=0\)です。よって、\(N+1\)個の線形独立なベクトルが見つかり、次元が\(N\)であることに矛盾しました。よって、\(\ell^p,\ell ^\infty\)は無限次元です。
数列空間\(\ell^p\)は、(可積分関数のなす)関数空間\(L^p\)と非常に良く似ています。ともに線形空間で、ノルムや内積を定めることができ、完備です。そして、両者とも無限次元です。
\[ \begin{aligned}\|x\|_{\ell^p}:=(\sum_{n=1}^\infty x_n^p)^{\frac{1}{p} }\end{aligned} \]
\[ \begin{aligned}\|f\|_{L^p}:=(\int |f(x)|^p dx)^{\frac{1}{p} }\end{aligned} \]
\[ \begin{aligned}\langle x,y\rangle_{\ell^2}:= \sum_{n=1} ^\infty x_n y_n\end{aligned} \]
\[ \begin{aligned}\langle f,g\rangle_{L^2}:= \int f(x)g(x) dx\end{aligned} \]
数列空間は無限次元のため、そのままでは線形代数で扱うことは少ないでしょう。
しかし、特定の漸化式を満たすような数列空間は、有限次元の部分空間となり、線形代数の枠組みで解くことができます。背後に無限次元の空間があっても、その部分空間が有限次元ならば、線形代数を使えるわけですね。
参考:漸化式(フィボナッチ数列)を線形代数(線形空間、固有ベクトル)で解く方法を解説
以上、数列空間l^pが線形空間となること、その性質としてノルム、内積、無限次元であることを紹介してきました。
今回はその値を実数\(\mathbb{R}\)としましたが、複素数\(\mathbb{C}\)としても同じことが示せます。
数列空間は、線形空間の例として、また関数解析の初歩的な例として扱いやすいものです。\(\ell ^p\)という記号を見ても、(ある意味で和が有限な)数列の集まりなのだな、と恐れずに扱えるようになってみてださい。
木村すらいむ(@kimu3_slime)でした。ではでは。
遊星社 (2006-05-01T00:00:01Z)
¥4,290
共立出版 (1980-11-01T00:00:01Z)
¥5,390