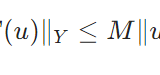線形作用素の有界性と連続性は同値であることの証明

どうも、木村（@kimu3_slime）です。

今回は、線形作用素について、有界性と連続性は同値であることの証明を紹介します。

定義
証明
線形でないとき
こちらもおすすめ

定義

\(X,Y\)をノルム空間とし、\(F:X \to Y\)を線形作用素（線形写像）とします。

\(F\)が有界であるとは、「すべての\(u \in X\)に対して、\(\|F(u)\|_Y \leq M \|u\|_X\)」を満たす\(M\)が存在することです。

\(F\)が\(X\)において（点列）連続であるとは、すべての\(u \in X\)に対し、\((u_n) \)を\(\lim_{n \to \infty} \|u_n-u\|_X=0\)を満たす\(X\)の点列とするならば、\(\lim_{n\to \infty}\|F(u_n)-F(u)\|_Y=0\)が成り立つことです。

証明

では、線形作用素\(F\)が有界であること、連続であることが同値であることを示しましょう。

まず、有界ならば連続を示します。

\(u \in X\)で、\((u_n) \)を\(\lim_{n \to \infty} \|u_n-u\|_X=0\)を満たす\(X\)の点列としましょう。\(F\)の線形性と有界性を用いれば、

\[\begin{aligned} &\|F(u_n)-F(u)\|_Y \\ &= \|F(u_n-u)\|_Y \\ & \leq M \|u_n-u\|_X \\& \to 0\quad(n \to \infty) \end{aligned}\]

となるので、\(F\)は連続です。

逆に、\(F\)が\(X\)において連続ならば有界であることを示しましょう。

対偶として、有界でないならば連続でないことを示します。

有界でないことから、すべての\(n \in \mathbb{N}\)に対し、\(\|F(u_n)\|_Y > n^2 \|u_n\|_X\)を満たす\(u_n \in X\)が存在します（\(M=n^2\)とした）。

\(u_n=0\)と仮定すると、\(F\)の線形性から\(F(u_n)=0\)となり、\(\|F(u_n)\|_Y = 0>0\)となり矛盾するため、\( u_n \neq 0\)です。ノルムの正定値性から、\(\|u_n\|_X \neq 0\)です。

そこで\(v_n := \frac{1}{n\|u_n\|_X}u_n\)と置きましょう。これは\(\|v_n\|_X = \frac{\|u_n\|_X}{ n\|u_n\|_X} = \frac{1}{n} \to 0\)です。

一方で、

\[\begin{aligned} &\|F(v_n)-F(0)\|_Y \\ &= \frac{\|F(u_n)\|_Y}{n \|u_n\|_X} \\ &> \frac{n^2 \|u_n\|_X}{n \|u_n\|_X}\\ &= n \\ & \to \infty \end{aligned}\]

となります。\(0\)に収束する\(X\)の点列\((v_n)\)について、その像\((F(v_n))\)が\(F(0)\)に収束しないので、\(F\)は\(X\)において連続ではありません。

よって、\(F\)は連続ならば有界です。

非有界と仮定すると、像は発散するけれども、もとの点列は収束するようなものが作れるわけですね。\(\frac{1}{n}\)のような点列は0に収束しますが、その\(n^2\)倍より大きな点列は\(\frac{n^2}{n}=n \)となり発散する、というアイデアです。