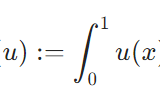放物型偏微分方程式の弱形式、弱解とは

どうも、木村（@kimu3_slime）です。

今回は、放物型偏微分方程式の弱形式とは何かを紹介します。

弱形式の導出
弱解の一意存在
こちらもおすすめ

弱形式の導出

放物型の偏微分方程式とは、

\[\frac{\partial u}{\partial t}-\Delta u = f(x,t)\]

\[u(x,t) = 0 \quad(x \in \partial \Omega) \]

\[u(x,0) = u_0(x) \]

と表される方程式です。\(\Omega \subset \mathbb{R}^N\)を有界で境界が\(C^2\)級の領域とします。

\(f(x,t)=0\)のときが熱方程式で、それを含むような一般的な方程式になっています。

熱の湧き出しや吸収を表す\(f(x,t)\)を非同次項（nonhomogeneous term）と呼び、全体を非同次の熱方程式（拡散方程式）とも呼びます。

この方程式の解の基本的な性質、存在と一意性などを調べるため、弱い意味での微分：弱微分を使って、弱い形（弱形式）に書き換えましょう。

まず、\([u(t)](x):=u(x,t)\)、\([f(t)](x):=f(x,t)\)と、\(t\)を止めるごとに\(x\)の関数が定まると見ることで、方程式の関数を時間付き関数空間の関数として捉えられます。

この表記によると、時間偏微分\(\frac{\partial u}{\partial t}(x,t)\)は、時間常微分\([\frac{du}{dt}(t)](x)\)となります。

境界で0の値を取る弱微分可能な関数\(\phi \in H_0 ^1\)を方程式にかけて

\[\frac{d u}{d t} \phi -\Delta u \phi= f \phi\]

部分積分しましょう。ラプラシアンの項は、

\[\begin{aligned} & \int_\Omega \Delta u(t) \phi dx\\ &= \int_{\Omega } (\sum_{k=1}^N \frac{\partial^2 u }{\partial x_k^2}) \phi dx \\&= -\int_{\Omega } \sum_{k=1}^N \frac{\partial u }{\partial x_k} \frac{\partial \phi }{\partial x_k} dx \\&= \int_{\Omega} \langle \nabla u, \nabla \phi \rangle dx\end{aligned}\]

となります。\(\nabla u =(\frac{\partial u}{\partial x_1},\dots,\frac{\partial u}{\partial x_N})\)は勾配ベクトル、\(\langle \cdot,\cdot \rangle\)はユークリッド内積です。

したがって、方程式は

\[ \int_{\Omega}\frac{d u}{d t} \phi dx +\int_{\Omega} \nabla u, \nabla \phi dx= \int_{\Omega} f \phi dx\]

となります。\(L^2\)内積を使って簡略化すれば、

\[ \langle \frac{du}{dt},\phi \rangle + \langle \nabla u, \nabla \phi \rangle = \langle f, \phi \rangle\]

と表せました。この方程式は\(t\)に依存しますが、積分を使って書かれているので、\(u\)の微分は弱微分として捉えても成り立つものですね。

この形を放物型方程式の弱形式（weak form）と呼び、すべての\(\phi \in H_0 ^1\)に対し方程式を満たすような\(u\)を弱解（weak solution）と呼びます。

弱解の一意存在

弱解が一意に存在する一般的な条件としては、次のものが知られています。

\(T>0\)、\(f \in L_{\mathrm{loc}}^2 ((0,\infty) ,H^{-1} (\Omega) )\)、\(u_0 \in L^2(\Omega)\)とする。

このとき、\( u \in L^2((0,T) ,H_0^1(\Omega))\)、\(\frac{du}{dt} \in L^2((0,T),H^{-1}(\Omega))\)、\(u \in C^0 ([0,T],L^2(\Omega))\)を満たす方程式の弱解\(u\)が一意に存在する。

\(L^2((0,T), H_0 ^1 (\Omega))\)は、時間方向に\(L^2\)で、時間を止めるごとに空間について弱微分可能で境界で0\(H_0 ^1\)という関数空間です。\(H^{-1}(\Omega)\)は\(H_0 ^1\)の双対空間で、\(\phi \in H_0^1\)との組で値を取る関数（線形汎関数）のなす空間です。

熱方程式における解の構成は、変数分離をしてフーリエ級数展開を利用するというものでした。

放物型方程式の弱解の構成は、それを一般化したガラーキン法（Galerkin’s method）という方法が知られています。ラプラシアン\(-\Delta\)の固有関数を使って近似解\(u_n(t)\)を作り、それが収束した結果が方程式を満たすことを示す、という流れですね。詳しくは、Robinson「Infinite-Dimensional Dynamical Systems」やEvans「Partial Differential Equations」を参照してください。

方法は異なりますが、

\[\frac{\partial u}{\partial t}-\Delta u = u-u^3\]

という形の反応拡散方程式にも、弱解が一意に存在することが知られています。

以上、放物型偏微分方程式の弱形式、弱解を紹介してきました。

放物型方程式の解の長期的な挙動：力学系、アトラクターを議論する上でも、解が一意に存在するとわかっていなければ空虚なものになるので、どういう意味で解が存在するのか知っておくと良いですね。

木村すらいむ（@kimu3_slime）でした。ではでは。