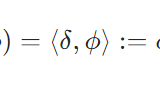どうも、木村(@kimu3_slime)です。
今回は、弱微分、ソボレフ空間とは何か、簡単な例を紹介します。
弱微分とは
弱微分は、従来の意味では微分可能でない関数に対しても定義できる、一般化された微分の考え方です。
その定義には、部分積分が満たす性質を用います。
実数\(\mathbb{R}\)の開区間\(\Omega =(a,b)\)において定義された、なめらかな(\(C^1\)級の)関数\(f,g\)について
\[\int_a^b f^{\prime}(x)g(x)dx =[f(x)g(x)]_{x=a}^{x=b}- \int_a^b f(x)g^{\prime}(x)dx\]
という等式が成り立ちます(部分積分)。
ここでもし\(g\)がテスト関数\(\phi\)ならば、\(\Omega\)の境界、端点における\(\phi(x)\)の値は0となるので、
\[\int_a^b f^{\prime}(x)\phi(x)dx =- \int_a^b f(x)\phi ^{\prime}(x)dx\]
となります。これはどんなテスト関数\(\phi\)を考えても、必ず成り立つ等式です。
逆に、部分積分の等式を満たすような関数を、弱微分として定義しましょう。
\(u,v\)を連続な関数(一般的には、局所可積分な関数\(u ,v\in L_{\mathrm{loc}}^1(\Omega)\))とします。\(u\)の弱微分(weak derivative)が\(v\)であるとは、どんなテスト関数\(\phi \in C_c ^\infty(\Omega)\)に対しても、
\[\int_\Omega v(x)\phi(x)dx =- \int_\Omega u(x)\phi ^{\prime}(x)dx\]
が成り立つことです。このとき、記号として\(v= u^{\prime}\)や\(v = \frac{du}{dx}\)と表します。
従来の微分の記号と全く同じで紛らわしいですが、混同しても問題は少ないです。強調するときは、弱い意味で(in weak sense)\(v= u^{\prime}\)と言います。
従来の意味での微分、ニュートン商の極限の存在による微分を、古典的な意味での微分(classical derivative)、強微分と呼ぶことにしましょう。
最も基本的な性質として、強微分可能(\(C^1\)級)ならば弱微分可能です。
なぜなら、さきほど議論したように、\(f\)が\(C^1\)級ならば、どんな\(\phi \in C_c ^\infty(\Omega)\)に対しても、部分積分により
\[\int_\Omega f^{\prime}(x)\phi(x)dx =- \int_\Omega f(x)\phi ^{\prime}(x)dx\]
が成り立つからです。\(f\)は弱微分可能であり、\(f\)の弱導関数は強導関数\(f^{\prime}\)と一致します。
もし強微分可能ならば弱微分可能で、強微分可能でない関数に対しても弱微分は定義できるので、弱微分は微分を一般化した概念として、一般化された微分(generalized derivative)とも呼ばれます。
弱微分の例
強い意味では微分できませんが、弱微分できる例として、絶対値関数
\[u(x)=|x|\]
を考えましょう。定義域は簡単のため\(\Omega =(-1,1)\)とします。
この関数は\(x=0\)において微分可能でなく、\(C^1\)級でないが、連続な関数(\(C^0\)級)の例となっています。
弱微分を求めるには、その定義式を書き下して
\[\int_{-1}^1 v(x)\phi(x)dx =- \int_{-1}^1 |x|\phi ^{\prime}(x)dx\]
これを満たす\(v\)を推測すれば良いです。
絶対値の部分は正負で場合分けして、右辺を計算してみます。部分積分によって、
\[\begin{aligned} &- \int_{-1}^1 |x|\phi ^{\prime}(x)dx \\ &= – \int_{-1}^0 (-x)\phi ^{\prime}(x)dx- \int_{0}^1 x\phi ^{\prime}(x)dx \\&= -[(-x)\phi(x)]_{-1}^0 +\int_{-1}^0 (-1)\phi(x)dx \\ &\quad -[x\phi(x)]_{0}^1 +\int_{0}^1 1 \phi(x)dx \\ &=\int_{-1}^0 (-1)\phi(x)dx +\int_{0}^1 1 \phi(x)dx \end{aligned}\]
となります。\(\phi\)はテスト関数なので\(\phi(-1)=\phi(1)=0\)、\(x=0\)においては\(-x,x\)の項が0になるので、境界の項が消えることに注意しましょう。
よって、
\[ v(x)= \left\{ \begin{array}{lr} -1 && (-1<x\leq 0) \\ 1 && (0<x< 1) \end{array} \right. \]
と定めれば、どんな\(\phi \in C_c ^\infty(\Omega)\)に対しても、
\[\int_{-1}^1 v(x)\phi(x)dx =- \int_{-1}^1 |x|\phi ^{\prime}(x)dx\]
を満たすので、\(u\)の弱微分は\(v\)である、\(u^{\prime}=v\)と求められました。
この関数は、強微分可能でないが、弱微分可能な例です。\(x=0\)のような不都合な一点を除いては微分可能な関数を、弱微分可能な関数として受け入れられるわけです。
これが可能になったのは、微分の定義を、極限の存在によるものではなく、テスト関数との関係性(積分)によって表したからですね。積分の等式は、関数の区間における連続的な:大域的な値を捉えますが、1点における値:局所的な値を無視できるのです。
ちなみに、この関数の弱微分の原点での値\(v(0)\)は一意には定まりません。\(v(0)\)がどんな値であっても、それは\(|x|\)の弱微分です。
これは弱微分には複数の可能性があって、何でも良いと言っているわけではありません。\(-1<x<0,0<x<1\)における弱微分の値は、さきほど定義した\(-1,1\)でなければなりません。
弱微分は、もし存在するならば、測度0の集合を除いて一意です。つまり、\(u\)の弱微分を\(v,w\)とすると、\(v,w\)はほとんど至る所で一致します。この用語の理解には、ルベーグ積分の知識が必要です。
高階の弱微分、多変数の弱微分
関数\(u\)の2階の弱微分、3階の弱微分、\(k\)階の弱微分\(v\)は、すべての\(\phi \in C_c ^\infty\)に対して
\[\int_\Omega v(x)\phi(x)dx = \int_\Omega u(x)\phi ^{\prime \prime}(x)dx\]
\[\int_\Omega v(x)\phi(x)dx =- \int_\Omega u(x)\phi ^{\prime\prime \prime}(x)dx\]
\[\int_\Omega v(x)\phi(x)dx =(-1)^k \int_\Omega u(x)\phi ^{(k)}(x)dx\]
を満たす関数としてそれぞれ定義されます。
部分積分を1回、テスト関数に微分を1回押し付けるごとに、符号が\(-1\)されるので、高階の弱微分の定義には\(-1\)の微分回数乗がかかるわけです。
ここまでは1変数の弱微分について話してきましたが、多変数でも同様です。
開集合\(\Omega \subset \mathbb{R}^n\)を定義域する\(C^1\)級の関数\(u\)、テスト関数\(\phi \in C_c ^\infty(\Omega)\)については、ガウスの発散定理から導かれる多変数の部分積分
\[\int_\Omega \frac{\partial u}{\partial x_i}\phi dx =\int_{\partial \Omega}u\phi \nu_i dS – \int_\Omega u \frac{\partial \phi}{\partial x_i}dx\]
が成り立ちます。\(\phi\)は境界での値が0となるので、
\[\int_\Omega \frac{\partial u}{\partial x_i}\phi dx =- \int_\Omega u \frac{\partial \phi}{\partial x_i}dx\]
を満たすわけです。
さきほどの議論と同様に、関数\(v\)が、すべての\(\phi \in C_c ^\infty(\Omega)\)に対して、
\[\int_\Omega v\phi dx =- \int_\Omega u \frac{\partial \phi}{\partial x_i}dx\]
を満たすとき、弱(偏)微分可能といい、\(v= \frac{\partial u}{\partial x_i}\)と表します。
高階の弱偏微分の定義も同様です。
ソボレフ空間
連続な関数のなす空間は\(C^0\)、\(k\)階微分可能で導関数が連続な関数のなす空間は\(C^k\)といった記号がありました。
これと同じ発想で、\(k\)階弱微分可能かつ\(p\)乗可積分な関数のなす空間を、
\[W^{k,p}(\Omega) = \{ u \in L^{p}(\Omega) \mid uはk階弱微分可能で、\\\quad k階までのすべての導関数が L^p の要素\}\]
と定義しましょう。これは線形空間の定義を満たし、ソボレフ空間(Sobolev space)と呼ばれています。数学者のセルゲイ・ソボレフに由来する名前です。
\(W\)の右上にある1番目の変数\(k\)が弱微分の回数、2番目の変数\(p\)が積分可能性を表しています。
定義から、可積分関数のなす空間\(L^p\)の部分集合なので、常に\(W^{k,p}(\Omega) \subset L^{p}(\Omega)\)が成り立ちます。
例えば、絶対値関数は\(|x| \in W^{1,2}(\Omega)\)です。
1階弱微分可能であることは、既に調べました。
また、定義域を\(\Omega=(-1,1)\)とする場合、\(|x|\)も弱導関数\(v\)も、2乗可積分です。一般に、連続な関数は有界な閉区間\([-1,1]\)上で最大値を持つので、\(|x|\)は2乗積分可能です。弱導関数については、
\[\begin{aligned} & \|v\|^2_{L^2(\Omega)}\\ &= \int _{-1} ^1 |v(x)|^2 dx \\&= \int_{-1}^0 (-1)^2 dx + \int_0^1 1^2 dx \\&=2 \\&<\infty \end{aligned}\]
となるので。
ソボレフ空間のうち、特に\(p=2\)のケースは良い性質を持ち頻繁に利用されるため、\(H^k(\Omega) := W^{k,2}(\Omega)\)という記号があります。
例えば、\(|x| \in H^1(\Omega )\)です。
\(\Omega\)が有界で、かつその境界まで込みで関数が連続的微分可能ならば、弱微分可能かつ\(p\)乗可積分となります。例えば、
\[C^k([-1,1]) \subset W^{k,p}([-1,1]) \subset L^p([-1,1])\]
です。このケースでは、ソボレフ空間は、連続関数の空間\(C^k\)と可積分関数の空間\(L^p\)の中間のようなものと言えますね(一般にはもう少し複雑ですが)。
ソボレフ空間\(W^{k,p}\)は、適切なノルムを定めることで、完備なノルム空間(バナッハ空間)になることが知られています。
また、\(p=2\)のときは、適切な内積を定めることで、\(H^k=W^{k,2}\)は完備な内積空間(ヒルベルト空間)になることが知られています。
ソボレフ空間については、他の関数空間との関連性(ソボレフの埋め込み定理)や、なめらかな関数による近似など重要な話題がありますが、長くなるので別記事にて紹介予定です。
以上、弱微分、ソボレフ空間とは何か、簡単な例を紹介してきました。
弱微分は、従来の意味で微分できる性質が満たす積分を使った等式:部分積分によって定義されます。
それによって、強い意味では微分できない絶対値関数のような関数を、弱微分可能なものとして扱えるようになりました。
微分可能な関数のなす空間があるように、弱微分可能(かつ可積分な)関数のなす空間は、ソボレフ空間\(W^{k,p}\)と呼ばれています。
微分の定義を一般化すると、偏微分方程式を強い意味では微分できない関数に対しても定義できる形(弱形式)にでき、弱い意味での解:弱解が定義できます。これによって、より一般的な偏微分方程式の解の構成が可能になるわけです。
その話はまた別記事ですが、入り口として弱微分やソボレフ空間の話が知ってもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)
こちらもおすすめ
連続関数、可積分関数の線形空間(関数空間)、微分と積分の線形性とは