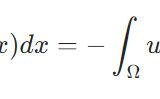どうも、木村(@kimu3_slime)です。
今回は、超関数、超関数微分とは何か、ディラックのデルタ関数を例に紹介します。
超関数とは
通常の関数と超関数
超関数は、テスト関数との積分を用いて定義される、関数の一般化です。
通常の関数\(f:\mathbb{R}\to \mathbb{R}\)から、超関数の例を構成してみましょう。テスト関数\(\phi\)を変数とする関数\(T_f:C_c^\infty(\mathbb{R}) \to \mathbb{R}\)を、
\[T_f (\phi): = \int_{\mathbb{R}}f(x) \phi (x)dx \]
と定義します。例えば、\(f(x)=1\)という恒等関数で、\(\phi\)の全体での積分が1となるとき、\(T_f (\phi)=1\)です。
関数のインプット\(\phi\)に対し、実数\(\mathbb{R}\)を対応させていますね。このように、関数を変数とし、値が数であるような写像は、汎関数(functional)と呼ばれるものです。
さきほど定義した汎関数\(T_f\)は、次のような良い性質を持っています。積分の線形性です。
- 線形性
- すべての\(\phi_1,\phi_2 \in C_c^\infty(\mathbb{R}) \)に対し、\(T(\phi_1+\phi_2) =T(\phi_1)+T(\phi_2)\)
- すべての\(\lambda \in \mathbb{R}\)、\(\phi \in C_c^\infty(\mathbb{R}) \)に対し、\(T(\lambda \phi)=\lambda T(\phi)\)
- 連続性
- \((\phi_n)\)が\(\phi\)に\(C_c^\infty(\mathbb{R})\)において収束するならば、\((T(\phi_n))\)は\(T(\phi)\)に収束する
この条件を満たす汎関数は、線形汎関数(linear functional)、特に有界線形汎関数と呼ばれます。
特に、定義域がテスト関数\(C_c ^\infty\)であるような有界線形汎関数を、シュワルツの超関数(distribution)と呼びます。
通常の関数\(f\)は、さきほどの積分との対応\(T_f\)として見ることで、超関数と見なすことができます。
そして、テスト関数との積の積分、つまり積分による内積の形になっているので、しばしば関数の内積の記号\(\langle \cdot, \cdot \rangle \)
\[\langle T_f ,\phi \rangle:=T_f (\phi) \\= \int_{\mathbb{R}}f(x) \phi (x)dx \]
を用いて対応を表します。通常の関数に対して積分の内積\(\langle f,g \rangle\)が考えられるように、超関数\(T\)に対しては\(\langle T, \phi \rangle\)が考えられるわけです。
超関数としてのデルタ関数
超関数を考えるモチベーションのひとつは、ディラックのデルタ関数のような関数を、超関数の枠組みで扱えることです。
瞬間的な衝撃を表す「関数」として、
\[ \begin{aligned}\delta (t)= \begin{cases}\infty & (t=0 )\\ 0& (t \neq 0)\end{cases}\end{aligned} \]
\[ \begin{aligned}\int_{-\infty} ^\infty \delta (t)dt =1\end{aligned} \]
を満たすようなものを考えたいです。
しかし、これは通常の意味での関数としては存在しません。原点以外の値が0となる関数は、全体で積分しても0で、1になりません。
そこで、
\[ \begin{aligned}f_d(t)= \begin{cases}\frac{1}{d} & (0 \leq t \leq d)\\0 & (それ以外)\end{cases}\end{aligned} \]
と、総積分が1であるまま、\(d\to 0\)で「デルタ関数」に近づくような関数と、テスト関数\(\phi\)の積分を計算してみましょう。
詳細は省略しますが、\(f_d\)は原点付近以外で0なので、
\[ \begin{aligned} \lim_{d \to 0} \int_0 ^\infty f_d(t) \phi(t)dt = \phi(0)\end{aligned} \]
と原点での値が取り出されます。したがって、デルタ関数は
\[ \begin{aligned}\int_0 ^\infty \delta(t) \phi (t)dt =\phi(0)\end{aligned} \]
という対応関係として見ることができれば良さそうです。
通常の関数ではこれは関数ではありませんが、テスト関数\(\phi\)を変数とすれば関数として見ることができます。
そこで、デルタ関数\(\delta: C_c ^\infty(\mathbb{R}) \to \mathbb{R}\)を
\[\delta (\phi) = \langle \delta ,\phi \rangle := \phi(0) \]
と定義しましょう。これは超関数の定義を満たします。
例えば線形性については、関数の和とスカラー倍の定義に注意すれば、
\[\delta(\phi_1+\phi_2) = (\phi_1+\phi_2)(0) \\ = \phi_1(0)+\phi_2(0)= \delta(\phi_1)+\delta(\phi_2)\]
\[\delta(\lambda \phi) = (\lambda \phi)(0) \\ = \lambda (\phi(0))= \lambda \delta(\phi)\]
となるので。
内積の記号を用いた表現は、
\[ \langle \delta ,\phi \rangle \\= \begin{aligned}\int_{-\infty} ^\infty \delta \phi (t)dt =\phi(0)\end{aligned} \]
という原点での値を取り出す役割として見ることができますね。
中心が原点\(x=0\)ではなく、\(a \in \mathbb{R}\)として
\[\delta_a (\phi) := \phi(a) \]
と定めれば、\(\delta _a\)も超関数です。多次元でも同様に定義できます。
超関数の微分とは
微分の一般化
通常の意味では微分できないような関数、さらには導関数が通常の意味では関数にならないケースであっても、微分を定義することができます。
もし\(f\)が\(C^1\)級の関数ならば、テスト関数\(\phi\)と部分積分をすると、テスト関数の効果によって境界の項が消えて、
\[ \langle f^{\prime} ,\phi \rangle = \int_{-\infty}^\infty f^{\prime}(x)\phi(x)dx \\ = – \int_{-\infty}^\infty f(x)\phi^{\prime}(x)dx =-\langle f,\phi^\prime \rangle\]
となります。
この関係式を用いて、微分可能でない関数に対しても弱い意味での微分:弱微分を定義できました。
さらにこの関係式は、\(f\)を超関数に置き換えれば、微分の定義式と見ることができるのではないでしょうか。
\(T,S\)を超関数とし、すべての\(\phi\in C_c ^\infty\)に対し、
\[ \langle S ,\phi \rangle =-\langle T,\phi^\prime \rangle\]
を満たすとき、\(S\)を\(T\)の超関数の意味での微分、超関数微分(distributional derivative)といい、\(S=T^{\prime}\)と表します。
通常の微分可能な関数\(f\)は、超関数\(T_f\)として見ることで、超関数微分可能です。しかし、超関数微分は通常の微分とは異なるケースもあります。
ヘビサイドの微分がデルタ
ヘビサイド関数(単位ステップ関数)
\[ \begin{aligned}H(x)= \begin{cases}0 & (x \leq 0 )\\1 & (x>0)\end{cases}\end{aligned} \]
を考えましょう。

この関数は原点において微分不可能です。それどころか、連続ですらありません。
しかし、ヘビサイド関数は超関数微分可能です。
もし「微分可能」と捉えられるならば、原点での変化率はなんでしょうか? 一瞬で0から1に変化するのですから、変化率が\(\infty\)、つまりデルタ関数になるのではないかと予想できます。
実際、その予想が正しいことを、計算によって確かめましょう。
超関数の意味で\(H^{\prime}=\delta\)とは、すべての\(\phi \in C_c ^\infty\)に対し、\[ \langle \delta ,\phi \rangle =-\langle H,\phi^\prime \rangle\]
を満たすことでした(\(H\)を超関数とみなしています)。
関数と記号の定義を思い出して、両辺を変形しましょう。
\[\langle \delta ,\phi \rangle =\phi(0) \]
\[\begin{aligned} &-\langle H,\phi^\prime \rangle \\ &= -\int_{-\infty}^\infty H(x)\phi^{\prime}(x)dx \\ &= -\int_{-\infty} ^0 0 \cdot \phi^{\prime}(x)dx -\int_0 ^\infty 1 \cdot \phi^{\prime}(x)dx \\&= -\int_0 ^\infty \phi^{\prime}(x)dx \\&= – [\phi(x)]_0 ^\infty \\&= -\lim_{x\to \infty}\phi(x) + \phi(0) \\&= \phi(0)\end{aligned}\]
となり、両辺が一致しました。\(\phi\)はテスト関数なので、無限遠方での値は0であることに注意。
以上、超関数、超関数微分とは何か、ディラックのデルタ関数を例に紹介してきました。
瞬間的な衝撃やジャンプの変化率など特異な現象を捉えるためには、ディラックのデルタ関数が必要ですが、それをテスト関数との積分を用いて一般的に定式化したものが超関数です。
超関数は単に定義できるだけでなく、今回示したような微分の概念、ラプラス変換やフーリエ変換を定義でき、微分方程式への応用を持ちます。
今回の話は正確に理解するのは難しいかもしれませんが、超関数やその微分が、通常の関数や微分の一般化として定義されること、そこでテスト関数や部分積分のアイデアが生きていることが伝われば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)
こちらもおすすめ
連続関数、可積分関数の線形空間(関数空間)、微分と積分の線形性とは