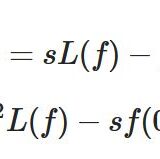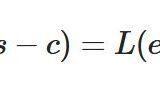どうも、木村(@kimu3_slime)です。
今回は、単位ステップ関数(ヘビサイド関数)とは何かを紹介し、そのラプラス変換、微分方程式への応用を紹介します。
単位ステップ関数とは
単位ステップ関数(unit step function)とは
\[ \begin{aligned}H(t)= \begin{cases}0 & (t \leq 0 )\\1 & (t>0)\end{cases}\end{aligned} \]
と表される関数です。ヘビサイドのステップ関数(Heaviside step function)、単にヘビサイド関数とも。

\(t=0\)において値が急に変わる、不連続な関数ですね。これは電気回路におけるスイッチの切り替えによる電圧の変化など、さまざまな現象を表すために使えます。\(t=0\)での値は、しばしば\(\frac{1}{2}\)としたり、未定義としたり、文脈に応じて変わるでしょう。
より一般に、\(A\)を集合として
\[ \begin{aligned}I_A(x)= \begin{cases}1 & (x \in A )\\0 & (x \not \in A)\end{cases}\end{aligned} \]
と表される関数\(I_A\)を、\(A\)の指示関数(indicator function)、特性関数(characteristic function)と呼びます。単位ステップ関数は、\(A=(0,\infty]\)とした特殊な指示関数として見ることができますね\(H= I_{(0,\infty]}\)。
(指示関数の線形結合は単関数、階段関数と呼ばれ、ルベーグ積分論において近似の基本となる関数です)
単位ステップ関数を使って、\(0<t<a \)ならば\(1\)、\(t \geq a\)ならば\(0\)の関数を作ってみましょう。
そうするには、\(f(t)=H(t)-H(t-a)\)とすれば良いですね。\(0<t<a\)のときは\(H(t)\)のみが機能します。\(t \geq a \)ならば\(H(t)-H(t-a)=1-1=0\)です。これは方形波パルスと呼ばれます。
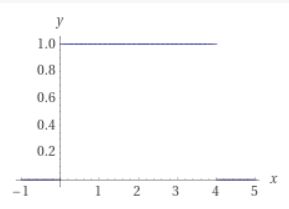
変数を\(a>0\)だけずらした単位ステップ関数(遅延つき単位ステップ関数)
\[ \begin{aligned}H(t-a)= \begin{cases}0 & (t \leq a )\\1 & (t>a)\end{cases}\end{aligned} \]
は、他の関数を組み合わせるのに使いやすいです。
ラプラス変換
単位ステップ関数\(H(t-a)\)のラプラス変換を求めてみましょう。
\(t \geq a\)以降のみで関数が値を持つことに注意すれば、
\[ \begin{aligned} L(H(t-a))&=\int _0 ^\infty e^{-st} H(t-a)dt\\ &= \int _a ^\infty e^{-st} \cdot 1 dt\\ &=[-\frac{1}{s}e^{-st}]_a ^\infty\\ &= \frac{e^{-as}}{s}\end{aligned} \]
となります。
微分方程式への応用
RL直列回路の微分方程式を考えましょう。
\[ \begin{aligned}\frac{dI}{dt}+\frac{R}{L}I =\frac{E}{L}\end{aligned} \]
簡単のため、\(R=2,L=1\)とします。今回は単位ステップ関数を使って、\(E(t)=H(t)-H(t-a)\)と表される起電力を考えましょう。一定時間までは定圧ですが、一定時間後に電源が切れるような状況を想定しています。
つまり、微分方程式
\[ \begin{aligned}\frac{dI}{dt}+2I =H(t)-H(t-a)\end{aligned} \]
微分のラプラス変換により
\[ \begin{aligned}L(\frac{dI}{dt})=sL(I)-I(0)\end{aligned} \]
で、単位ステップ関数のラプラス変換より
\[ \begin{aligned}L(H(t)-H(t-a))= \frac{1}{s}-\frac{e^{-as}}{s}\end{aligned} \]
です。したがって、方程式をラプラス変換すれば
\[ \begin{aligned}sL(I)-I(0)+2L(I)= \frac{1}{s}-\frac{e^{-as}}{s}\end{aligned} \]
となり、\(L(I)\)について整理すると
\[ \begin{aligned}L(I)= \frac{I(0)}{s+2}+\frac{1}{s(s+2)}-\frac{e^{-as}}{s(s+2)}\end{aligned} \]
です。部分分数分解\(\frac{1}{s(s+2)}= \frac{1}{2s}-\frac{1}{2(s+2)}\)を使って整理すると、
\[ \begin{aligned}L(I)= \frac{1}{2}(\frac{2I(0)-1}{s+2}+\frac{1}{s}\\-\frac{e^{-as}}{s}+\frac{e^{-as}}{s+2})\end{aligned} \]
となりました。これをラプラス逆変換しましょう。
指数関数のラプラス変換
\[ \begin{aligned}L(e^{bt})= \frac{1}{s-b}\end{aligned} \]
と第1シフト定理(s推移法則)
\[ \begin{aligned}L(e^{ct}f(t)) = L(f)(s-c)\end{aligned} \]
より
\[ \begin{aligned}L(e^{-2t }H(t-a))
\\ = L(H(t-a))(s+2)
\\=\frac{e^{-a(s+2)}}{s+2}\end{aligned} \]
を使います。すると、
\[ \begin{aligned}I(t)=\frac{1}{2} ((2I(0)-1)e^{-2t}+1\\ -H(t-a)+e^{-2(t-a) }H(t-a))\end{aligned} \]
と解が得られました。
特に、\(I(0)=0\)、\(a=4\)のときは
\[ \begin{aligned}I(t)= \begin{cases}\frac{1}{2} (-e^{-2t}+1 )& (0 <t\leq 4 )\\ \frac{1}{2} (-e^{-2t}+e^{-2(t-4)} ) & (t>4)\end{cases}\end{aligned} \]
となります。
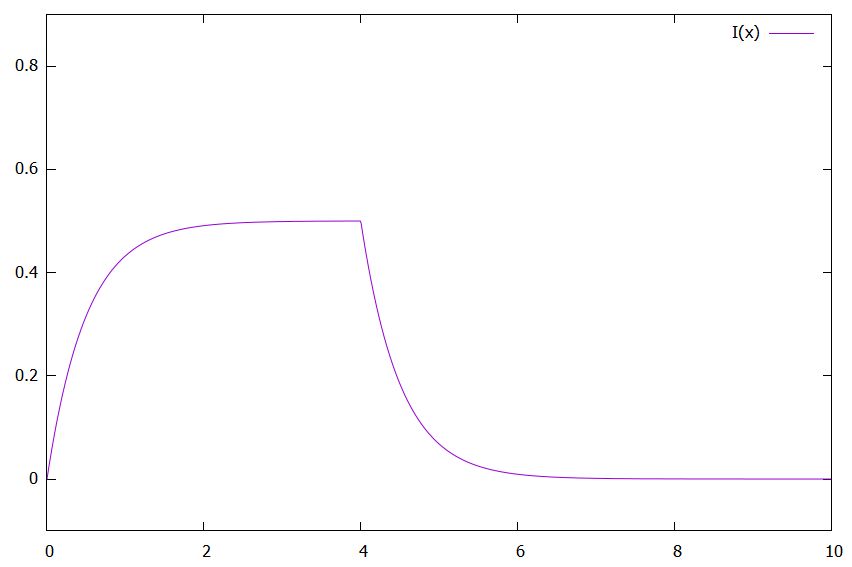
最初は一定の電圧によって電流は\(1/2\)に近づいていきますが、\(t=4\)で電源が切れて、その後は電流が減っていき\(0\)に近づくのがわかりますね。
以上、単位ステップ関数とは何か、そのラプラス変換と微分方程式への応用を紹介してきました。
スイッチによって変化するような不連続なインプットを持つ方程式を解くときに、ラプラス変換が便利なのが感じられますね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)