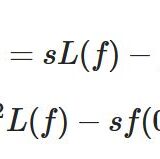どうも、木村(@kimu3_slime)です。
今回は、ラプラス変換とは何か、その定義と微分方程式への応用を紹介します。
手っ取り早く全体像をつかむための導入なので、公式の導出などは一旦省略します。
ラプラス変換とは
\(f(t)\)を実数値関数とします。\(f\)のラプラス変換(Laplace transform)は、
\[ \begin{aligned}L(f)(s) := \int_0 ^\infty e^{-st}f(t)dt\end{aligned} \]
によって定義されます。積分する変数は\(t\)であり、右辺はパラメータ\(s\)に依存している、つまり\(s\)の関数であることに注意しましょう。
ラプラス変換によって、\(f\)という関数は、\(L(f)\)という\(s\)を変数とする関数に変わります。これはフーリエ変換と同じく、積分変換(integral transform)の一種です。そして\(L\)は関数を関数に対応させる写像で、積分作用素と呼ばれるものの一種です。
例として、定数関数\(f(t)= 1\)をラプラス変換してみましょう。すると、
\[ \begin{aligned}L(f)(s)= \int_0 ^\infty e^{-st}dt \\ =[-\frac{1}{s}e^{-st}]_0 ^\infty \\ = \frac{1}{s} \end{aligned} \]
になります。つまり、\(L(f)(s)= \frac{1}{s}\)という関数に変わりました。
これを逆に戻す操作\(L^{-1}\)を、逆ラプラス変換(inverse Laplace transform)といいます。例えば、\(L^{-1}(\frac{1}{s})= f\)(定数関数)です。
積分の線形性によって、ラプラス変換作用素\(L\)も線形作用素になり、\(L(af +g)=aL(f)+L(g)\)といったようにバラバラに計算できます。
なぜラプラス変換を考えるのでしょうか。
そのひとつは、初等関数、関数の微分のラプラス変換・逆ラプラス変換の結果が簡単であり、それを使って微分方程式が解けるからです。
例えば、初等関数のラプラス変換の結果は、教科書やWikipediaにまとまっています。積分計算の方法を知らなくても、この表を使えば、ラプラス変換、逆ラプラス変換を行うことができます。
また、関数の微分のラプラス変換は次のような都合の良い性質を持っています。
\[ \begin{aligned}L(f^{\prime})= sL(f)-f(0)\end{aligned} \]
\[ \begin{aligned}L(f^{\prime \prime})=s^2 L(f)-sf(0)-f^{\prime}(0)\end{aligned} \]
ラプラス変換を微分に対して施すと、結果は\(s\)の多項式となります。
これを使うと、非同次の微分方程式、例えば定数係数の2階線形微分方程式
\[ \begin{aligned}\frac{d^2 x}{dt^2}+a\frac{dx}{dt}+bx= r(t)\end{aligned} \]
を通常とは違う方法で解くことができます。
両辺をラプラス変換して整理すると、\(L(x(t)) =(sの有理式)\)という形(補助方程式 subsidiary equation)が得られます。(右辺は有理式とは限らないのですが、簡単な例では有理式であることが多い)
これをさらに整理し、右辺を逆ラプラス変換しやすい形(既知の形)に変形します。そして、逆ラプラス変換を施せば、\(x(t)= L^{-1}(L(x(t)))= L^{-1}(sの有理式)\)と解が求められるわけです。
微分方程式を解くという問題を、「ラプラス変換し、代数方程式を解いて、それを逆ラプラス変換する」という問題に書き換えるわけですね。これは普通に微分方程式を解くよりも簡単な場合があります。特に方程式の右辺に非同次項\(r(t)\)があるケースがそうです。
ラプラス変換で微分方程式を解く
ラプラス変換は、非同次項、時間変化するインプットを持つ微分方程式を解くのに便利です。
例として、次の強制振動の方程式をラプラス変換によって解いてみましょう。
\[ \begin{aligned}\frac{d^2x}{dt^2}+4 x = \cos t\end{aligned} \]
通常の方法だと、まず同次方程式を解き、その後何らかの方法(係数変化法、未定乗数法など)で特殊解を得る必要があります。
ラプラス変換では、微分のラプラス変換と、ラプラス変換表を使って計算します。
\[ \begin{aligned}L(f^{\prime \prime})=s^2 L(f)-sf(0)-f^{\prime}(0)\end{aligned} \]
を当てはめると、
\[ \begin{aligned}L(\frac{d^2x}{dt^2})= s^2L(x)-sx(0)-\frac{dx}{dt}(0)\end{aligned} \]
で、
\[ \begin{aligned}L(\cos \omega t)= \frac{s}{s^2+\omega^2}\end{aligned} \]
を当てはめると
\[ \begin{aligned}L(\cos t)=\frac{s}{s^2+1}\end{aligned} \]
です。これらを微分方程式に代入すれば(ラプラス変換すれば)、
\[ \begin{aligned}s^2L(x)-sx(0)-\frac{dx}{dt}(0) \\+4L(x)=\frac{s}{s^2+1}\end{aligned} \]
となります。これが補助方程式です。\(L(x)\)について整理すれば
\[ \begin{aligned}L(x)=\frac{s}{s^2+4}x(0)\\+\frac{1}{s^2+4}\frac{dx}{dt}(0)+\frac{s}{(s^2+1)(s^2+4)}\end{aligned} \]
となりました。場合によっては部分分数分解をして、右辺を扱いやすい形にする必要があります。
今回は、既に解けた形です。ラプラス変換の表を眺めて、逆ラプラス変換をしましょう。
\[ \begin{aligned}L(\cos \omega t)=\frac{s}{s^2+\omega ^2}\end{aligned} \]
\[ \begin{aligned}L(\frac{1}{\omega} \sin \omega t)= \frac{1}{s^2+\omega ^2}\end{aligned} \]
\[ \begin{aligned}L(\frac{1}{b^2-a^2}(\cos at -\cos bt))\\=\frac{s}{(s^2+a^2)(s^2+b^2)}\\ ただし a^2 \neq b^2\end{aligned} \]
を用いて、両辺を逆ラプラス変換します。すると、
\[ \begin{aligned}x(t)=(x(0)-\frac{1}{3})\cos 2t +\frac{\frac{dx}{dt}(0)}{2}\sin 2t +\frac{1}{3} \cos t\end{aligned} \]
と解が得られました。これは確かに普通の方法(未定係数法)で得た解と同じです。
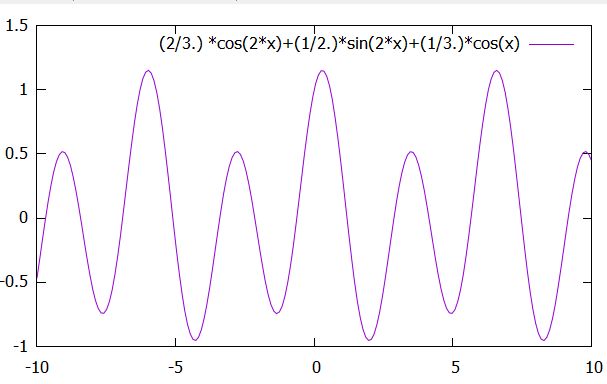
ラプラス変換だと、表に照らし合わせる必要はありますが、解く手順は簡単で、初期条件が明示的に組み込めているのが良いですね。特に、複雑なインプット\(r(t)\)にも対応できるのがラプラス変換の長所です。
以上、ラプラス変換とは何か、定義と微分方程式への応用を紹介してきました。
特に非同次の2階線形微分方程式を解くために、ラプラス変換が有効であることが感じられたと思います。公式やさらなる性質については、別記事で紹介予定です。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
こちらもおすすめ
連続関数、可積分関数の線形空間(関数空間)、微分と積分の線形性とは
非同次の2階線形微分方程式の解き方、未定係数法:強制振動を例に