どうも、木村(@kimu3_slime)です。
今回は、RLC直列回路の微分方程式の立て方、電流の求め方、減衰現象について紹介します。
予備知識:RL直列回路の微分方程式の立て方、電流の求め方、過渡現象
RLC回路の方程式
RLC直列回路(RLC circuit)とは、抵抗\(R\)、コイル(インダクター)\(L\)、コンデンサー(キャパシター)\(C\)を直列につないだ電気回路のことです。LCR回路とも。
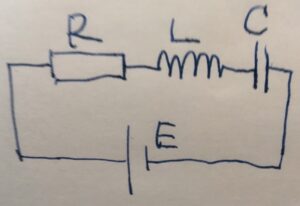
この回路の電流に関する微分方程式(回路方程式)を導いてみましょう。電流を\(I(t)\)とします。
抵抗による電圧低下は\(E_R = RI\)、コイルは\(E_L = L \frac{dI}{dt}\)、コンデンサーは\(E_C = \frac{1}{C}Q\)です。ここで\(Q\)はコンデンサーが蓄える電気量です。
電圧に関するキルヒホッフの第2法則により、
\[ \begin{aligned}E_R+E_L +E_C =E\end{aligned} \]
\[ \begin{aligned}RI +L \frac{dI}{dt} +\frac{1}{C}Q =E\end{aligned} \]
が成り立ちます。
今回は、電源が定圧の直流電源のケースを考えましょう(\(\frac{d}{dt}E=0\))。\(\frac{dQ}{dt}=I\)に注意して、方程式を\(t\)について微分し、整理すれば
\[ \begin{aligned}\frac{d^2 I}{dt^2} +\frac{R}{L}\frac{dI}{dt} +\frac{1}{LC} I =0\end{aligned} \]
という微分方程式が得られました。
微分方程式の解き方
この方程式は、同次形で定数係数の2階線形微分方程式なので、特性方程式を解くことで解が得られます。
参考:2階線形常微分方程式の解き方、学ぶ意味:熱方程式への応用を例に、線形微分方程式はなぜ指数関数e^{λt}と仮定して解いて良いか
力学の例では、おもりバネダンパ系の方程式は、RLC回路の方程式とよく似ていて、同じような結果が得られます。
\[ \begin{aligned}m\frac{d^2 x}{dt^2} = -kx -c\frac{dx}{dt}\end{aligned} \]
位置\(x(t)\)が電流\(I(t)\)に、質量\(m\)がインダクタンス\(L\)に、ダンパの減衰係数\(c\)が抵抗\(R\)に、ばね定数\(k\)が静電容量の逆数\(\frac{1}{C}\)に対応していますね。
参考:おもりバネダンパ系:減衰振動の運動方程式、微分方程式の解き方
RLC回路の微分方程式に対応する特性方程式は
\[ \begin{aligned}\lambda ^2 + \frac{R}{L}\lambda + \frac{1}{LC}=0\end{aligned} \]
で、これを解けば
\[ \begin{aligned}\lambda = \frac{-R \pm \sqrt{R^2-\frac{4L}{C}}}{2L}\end{aligned} \]
となります。つまり、\(R^2-\frac{4L}{C}\)の符号によって、解のようすは変わってきます。
過減衰
\(R^2-\frac{4L}{C}>0\)のとき、特性方程式は異なる2つの実数解を持ちます。したがって、微分方程式の解は
\[ \begin{aligned}x(t)= C_1 e^{\frac{-R + \sqrt{R^2-\frac{4L}{C}}}{2L}t}+C_2 e^{\frac{-R – \sqrt{R^2-\frac{4L}{C}}}{2L}t}\end{aligned} \]
となります。
指数部分がどちらも負なので、
\[ \begin{aligned}\lim_{t \to \infty} x(t)=0\end{aligned} \]
となります。抵抗による減衰が支配的な状態で、過減衰(overdamping)と呼ばれる現象です。
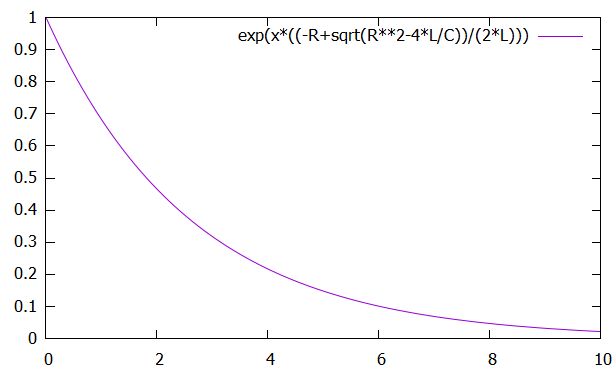
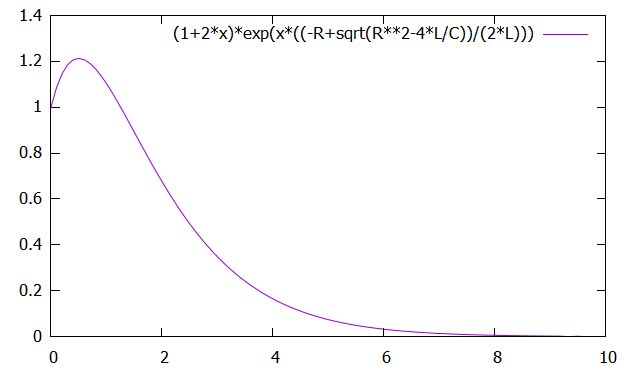
臨界減衰
\(R^2-\frac{4L}{C}=0\)のとき、特性方程式は重解です。そのため、微分方程式の解は
\[ \begin{aligned}x(t)= (C_1 +C_2 t)e^{\frac{-R }{2L}t}\end{aligned} \]
となります。
指数部分は負であり、多項式の増大より指数減衰の方が強いので、
\[ \begin{aligned}\lim_{t\to \infty}x(t)=0\end{aligned} \]
です。このときは臨界減衰(critical damping)と呼ばれます。
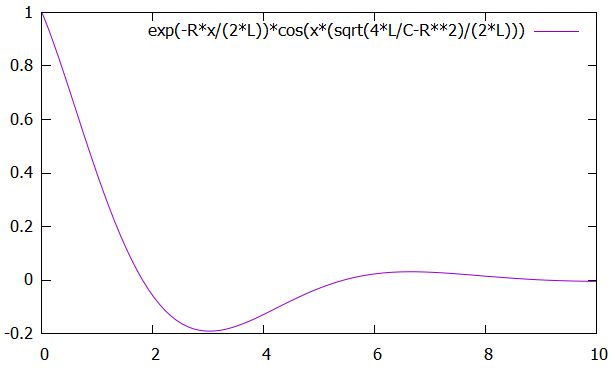
不足減衰:減衰振動
\(R^2-\frac{4L}{C}<0\)のとき、特性方程式は共役な複素数解を持ちます。その実部は\(-\frac{R}{2L}\)、虚部は\(\frac{\sqrt{\frac{4L}{C} – R^2}}{2L}\)なので、微分方程式の解は
\[ \begin{aligned}x(t) = e^{-\frac{R}{2L} t}(C_1 \cos (\frac{\sqrt{\frac{4L}{C} – R^2}}{2L} t)+C_2 \sin (\frac{\sqrt{\frac{4L}{C} – R^2}}{2L}t ))\end{aligned} \]
となります。
その大きさを評価すると、三角関数の部分は定数によって抑えられるので、
\[ \begin{aligned}|x(t) | \leq C_3 e^{ -\frac{R}{2L}t }\end{aligned} \]
です。三角関数によって振動しながら減衰していくようすは、不足減衰(underdamping)、減衰振動(damped oscillation)と呼ばれています。

以上、RLC直流回路の微分方程式の立て方、電流の求め方、減衰現象について紹介してきました。
今回は定圧電源による電流を考えましたが、周期的な交流電源\(E(t)= E_0 \cos \omega t\)を考えると、強制振動、うなりや共鳴といった現象が見られるようになります。
参考:非同次の2階線形微分方程式の解き方、未定係数法:強制振動を例に
RLC回路の方程式がおもりバネダンパ系の方程式と似ていることを知ると、方程式の解き方や減衰振動についてより理解しやすくなるでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
こちらもおすすめ
2階線形常微分方程式の解き方、学ぶ意味:熱方程式への応用を例に
線形微分方程式はなぜ指数関数e^{λt}と仮定して解いて良いか
おもりバネダンパ系:減衰振動の運動方程式、微分方程式の解き方
非同次の2階線形微分方程式の解き方、未定係数法:強制振動を例に