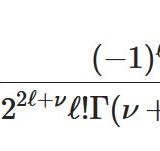どうも、木村(@kimu3_slime)です。
今回は、フロベニウスの方法について、次数0の第二種ベッセル関数の求め方を例に紹介します。
フロベニウスの方法とは
フロベニウスの方法(Frobenius’s method)とは、係数に特異性のある線形微分方程式の解を得る方法です。
\(b(x),c(x)\)を\(x=0\)において解析的とする。
\[ \begin{aligned} y^{\prime \prime}+\frac{b(x)}{x}y^{\prime} +(1- \frac{c(x)}{x^2})y =0\end{aligned} \]
と表される方程式は、
\[ \begin{aligned}y(x)=x^r \sum_{k=0}^\infty a_k x^k\end{aligned} \]
と表される解を少なくともひとつ持つ。
(もうひとつの解は、これと似た形で見つかる。)
これをベッセル方程式(Bessel’s equation)にあてはめると、
\[ \begin{aligned}x^2 y^{\prime \prime}+xy^{\prime} +(x^2-\nu ^2)y =0\end{aligned} \]
\[ \begin{aligned}J_n(x)= \sum_{\ell=0}^\infty \frac{(-1)^\ell }{2^{2\ell+n} \ell! (n+\ell)!} x^{2\ell +n }\end{aligned} \]
2階の線形微分方程式には、基本解(線形独立な)が2つ存在します。その一方は第一種ベッセル関数であるわけですが、もうひとつの解、第二種ベッセル関数を見つけましょう。
(次数が非整数のときは、第一種ベッセル関数\(J_\nu , J _{-\nu}\)は線形独立。次数が整数のとき、それらが線形独立でないので、第二種ベッセル関数を見つける必要があります。)
今回は簡単のため、\(\nu =0\)のケースを考えます。解が級数の形\(y(x)= \sum_{k=0}^\infty x^{k+r}\)と仮定して得られる次数\(r\)に関する方程式
\[ \begin{aligned} (r+\nu) (r-\nu)=0\end{aligned} \]
は決定方程式(indicial equation)と呼ばれました。
\(\nu =0\)のときは決定方程式は重解を持ち、そのときは次の形の解が見つかることが知られています。
決定方程式が重解\(r=r_1=r_2\)のときのフロベニウスの方法
\(y_1(x)= \sum_{k=0}^\infty x^{k+r}\)をひとつ解として、もうひとつの解は
\[ \begin{aligned}y_2(x)= y_1 (x) \log x +\sum _{k=1}^\infty b_k x^{k+r}\end{aligned} \]
と表せる。ただし、\(x \neq 0\)。
ベッセル方程式の解き方、第二種ベッセル関数
\(\nu =0\)のときのベッセル方程式
\[ \begin{aligned}x^2 y^{\prime \prime}+xy^{\prime} +x^2y =0\end{aligned} \]
をフロベニウスの方法で解いてみましょう。決定方程式の解は\(r=0\)で重解、ひとつの解は\(y_1(x)=J_0(x)\)です。もうひとつの解は
\[ \begin{aligned}y_2 (x)= J_0(x) \log x+\sum _{k=1}^\infty b_k x^{k} \end{aligned} \]
と表されます。方程式に代入し、係数\(b_k\)を求めていきましょう。
その微分は
\[ \begin{aligned}y_2^\prime = J_0 ^\prime \log x +\frac{J_0 }{x}+\sum_{k=1}^\infty k b_k x^{k-1}\end{aligned} \]
\[ \begin{aligned}y_2^{\prime\prime}= J_0^{\prime \prime} \log x +\frac{2J_0 ^{\prime}}{x}- \frac{J_0}{x^2}\\+ \sum_{k=1}^\infty k (k-1)b_k x^{k-2}\end{aligned} \]
となります。これを方程式に代入します。
\(\log\)のついた項に注目すると、\(J_0\)は解なので、
\[ \begin{aligned}(x^2 J_0^{\prime \prime} +xJ_0^\prime +J_0)\log x\\ =0\end{aligned} \]
となります。この結果が得られるように、\(\log\)の項を仮定したわけですね。
また、\(\frac{J_0 }{x}\)と\(- \frac{J_0}{x^2}\)の項も、足して0になります。よって、残る項は
\[ \begin{aligned}2J_0^\prime x + \sum_{k=1}^\infty k (k-1)b_k x^{k}\\+\sum_{k=1}^\infty k b_k x^{k}+\sum _{k=1}^\infty b_k x^{k+2}=0\end{aligned} \]
です。
\[ \begin{aligned}J_0(x)= \sum_{\ell=0}^\infty \frac{(-1)^\ell }{2^{2\ell} \ell! (\ell)!} x^{2\ell }\end{aligned} \]
の微分を計算すると、
\[ \begin{aligned}J_0^\prime (x)= \sum_{\ell=1}^\infty \frac{(-1)^\ell 2\ell }{2^{2\ell} \ell! (\ell)!} x^{2\ell -1 }\\= \sum_{\ell=1}^\infty \frac{(-1)^\ell }{2^{2\ell-1} \ell! (\ell -1)!} x^{2\ell -1 } \end{aligned} \]
です。これを方程式に戻して整理すれば、
\[ \begin{aligned} \sum_{\ell=1}^\infty \frac{(-1)^\ell }{2^{2\ell-2} \ell! (\ell -1)!} x^{2\ell } \\ + \sum_{k=1}^\infty k^2 b_k x^{k}+ \sum _{k=1}^\infty b_k x^{k+2} \\ =0\end{aligned} \]
となります(最初の項の係数に注意)。係数を比較しましょう。
\(x^1\)の項を見ると、\( b_1 =0\)です。また、奇数次数、\(k= 2\ell +1\)のとき、
\[ \begin{aligned}(2\ell +1)^2 b_{2\ell+1}+b_{2\ell -1}=0\end{aligned} \]
となります。\(b_1=0\)であることから、\(b_{2\ell+1}=0\)となって奇数次の係数はすべて消えます。
偶数次数\(k=2\ell\)のときの係数を比較すると、
\[ \begin{aligned} \frac{(-1)^\ell }{2^{2\ell-2} \ell! (\ell -1)!} +4\ell^2 b_{2\ell}+b_{2\ell-2}=0\end{aligned} \]
です。ただし、\(\ell=1\)のときは最後の項はなく、
\[ \begin{aligned}\frac{(-1)^1 }{2^{0} 1! 0!} +4 b_{2}=0\end{aligned} \]
となって、\(b_2 = \frac{1}{4}\)がわかります。続く係数を計算しましょう。
\[ \begin{aligned}b_4 = \frac{1}{4 \cdot 2^2} (-b_2+\frac{(-1)^{2-1} }{2^{2\cdot 2-2} 2! (2 -1)!} )\\ =\frac{(-1)}{ 2^4 \cdot 2! 2!}(1+\frac{1}{2}) \end{aligned} \]
\[ \begin{aligned}b_6 = \frac{1}{4 \cdot 2^3} (-b_4+\frac{(-1)^{3-1} }{2^{2\cdot 3-2} 3! (3 -1)!} )\\ =\frac{(-1)^{3-1}}{ 2^6 \cdot 3! 3!}(1+\frac{1}{2}+\frac{1}{3}) \end{aligned} \]
で、一般には
\[ \begin{aligned}b_{2\ell} =\frac{(-1)^{\ell-1}}{ 2^{2\ell} (\ell!)^2}(1+\frac{1}{2}+\cdots + \frac{1}{\ell}) \end{aligned} \]
となります。
よって、解は
\[ \begin{aligned}y_2(x)= J_0 (x)\log x \\ +\sum_{\ell=1}^\infty \frac{(-1)^{\ell-1}}{ 2^{2\ell} (\ell!)^2}(1+\frac{1}{2}+\cdots + \frac{1}{\ell})x^{2\ell} \end{aligned} \]
と求められました。この級数は\(x \neq 0\)で収束します(レシオテスト)。
特に、次のように係数を少し調整した解が用いられることが多いです。て
\[ \begin{aligned}Y_0(x):= a(y_2 +bJ_0)\end{aligned} \]
\(a= \frac{2}{\pi}\)、\(b= \gamma- \log 2\)としましょう。\(\gamma\)はオイラーのガンマ定数で、\(\gamma =\lim_{\ell \to \infty}(1+\frac{1}{2}+\cdots + \frac{1}{\ell} -\log \ell)\)と定義されます。すると、
\[ \begin{aligned}Y_0(x)= \frac{2}{\pi}((J_0(x)(\log \frac{x}{2} +\gamma) \\+\sum_{\ell=1}^\infty \frac{(-1)^{\ell-1}}{ 2^{2\ell} (\ell!)^2}(1+\frac{1}{2}+\cdots + \frac{1}{\ell})x^{2\ell} )\end{aligned} \]
となりました。このベッセル方程式の解\(Y_0\)は、次数0の第二種ベッセル関数(Bessel function of the second kind)、ノイマン関数(Neumann’s function)と呼ばれます。
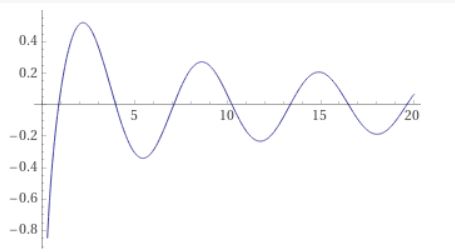
関数\(Y_0\)は、原点付近では\(\log x\)に近く、無限遠方では\(\sin x\)のような挙動をすることが知られています。
一般の次数の第二種ベッセル関数は
\[ \begin{aligned}Y_\nu = \frac{1}{\sin \nu \pi}(J_\nu (x) \cos \nu \pi – J_{-\nu}(x))\end{aligned} \]
\[ \begin{aligned}Y_n (x) = \lim_{\nu \to n}Y_\nu (x)\end{aligned} \]
と表されることが知られています。
第一種ベッセル関数と第二種のベッセル関数は線形独立であり、ベッセル方程式の一般解は
\[ \begin{aligned}y(x)=C_1 J_\nu (x)+C_2 Y\nu(x)\end{aligned} \]
と表すことができます。
また、第一種、第二種ベッセル関数を組み合わせた
\[ \begin{aligned}H_\nu^{(1)}(x) =J_\nu (x)+iY_\nu (x)\end{aligned} \]
\[ \begin{aligned}H_\nu^{(2)}(x) =J_\nu (x)-iY_\nu (x)\end{aligned} \]
複素数値の関数\(H_\nu^{(1)}\)は、ハンケル関数(Hankel function)、第三種ベッセル関数と呼ばれています。
以上、フロベニウスの方法によって、次数0のベッセル方程式の解、第二種のベッセル関数を求めてきました。
単なるべき級数では解は見つかりませんでしたが、そこで対数\(\log x\)の項を加えることで、2つ目の解を求められることがわかりましたね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
こちらもおすすめ
フロベニウスの方法とは:ベッセル方程式、第一種ベッセル関数を例に
線形微分方程式はなぜ指数関数e^{λt}と仮定して解いて良いか