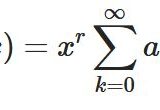第一種ベッセル関数のガンマ関数による表示式

どうも、木村（@kimu3_slime）です。

今回は、第一種ベッセル関数のガンマ関数による表示式を紹介します。

ベッセル方程式とは

\[ \begin{aligned}x^2 y^{\prime \prime}+xy^{\prime} +(x^2-\nu ^2)y =0\end{aligned} \]

という\(\nu \geq 0\)をパラメータとする方程式です。

\[ \begin{aligned}J_n(x)= \sum_{\ell=0}^\infty \frac{(-1)^\ell }{2^{2\ell+n} \ell! (n+\ell)!} x^{2\ell +n }\end{aligned} \]

と求められました。これを第一種ベッセル関数と言います。

ただし、この解は\(\mu =n\)、整数のケースを考えたものでした。今回は、一般の\(\mu\)、非整数のケースの表示式を得ましょう。

フロベニウスの方法で行った計算により、\(y(x)= \sum_{k=0}^\infty a_k x^{k+r}\)、\(r= \nu \)という解を考えると、

\[ \begin{aligned}a_{2\ell}=\frac{(-1)^\ell }{2^{2\ell} \ell! (\nu+1)\cdots(\nu+\ell)}a_{0}\end{aligned} \]

という関係式が成り立つことがわかっています。

分母がシンプルになるように\(a_0\)を指定したいわけです。\(\mu =n\)のときは\(a_0 =\frac{1}{2^n n!}\)としましたが、\(\mu\)が非整数のときは階乗によって整理することはできません。そこで、ガンマ関数

\[ \begin{aligned}\Gamma(x)=\int_0^\infty t^{x-1}e^{-t}dt\end{aligned} \]

を利用しましょう。\(x \geq 0\)としています。結果として、ガンマ関数は階乗\(n!\)を非整数に拡張した関数となっています（\(\Gamma (n)= (n-1)!\)）。

ガンマ関数の基本的な性質として、関数等式

\[ \begin{aligned}\Gamma (x+1)= x \Gamma(x)\end{aligned} \]

があります。部分積分をすることで

\[ \begin{aligned} \Gamma(x+1)&= \int_0^\infty t^{x}e^{-t}dt \\&= -[t^x e^{-t}]_0 ^\infty + x \int _0 ^\infty t^{x-1}e^{-t}dt \\ &=x \Gamma(x)\end{aligned} \]

と示せますね。\(\Gamma(1)=1\)と合わせると、\(\Gamma (n)= (n-1)!\)がわかります。

これを使って、ベッセル関数の係数を計算しましょう。例えば、\((\nu+1)\Gamma(\nu+1) = \Gamma(\nu+2)\)、\((\nu +2)\Gamma(\nu+2)= \Gamma(\nu+3)\)といった関係が成り立ちます。

\(a_0 = \frac{1}{2^\nu \Gamma(\nu)}\)とすると、

\[ \begin{aligned}a_{2\ell}\\=\frac{(-1)^\ell }{2^{2\ell} \ell! (\nu+1)\cdots(\nu+\ell)}\frac{1}{2^\nu \Gamma(\nu)}\\ \frac{(-1)^\ell }{2^{2\ell+\nu} \ell! \Gamma(\nu +\ell +1)}\end{aligned} \]

です。よって、ベッセル方程式の解は

\[ \begin{aligned}J_\nu(x)= \sum_{\ell=0}^\infty \frac{(-1)^\ell }{2^{2\ell+\nu} \ell! \Gamma(\nu +\ell +1)}x^{2\ell +\nu }\end{aligned} \]

と求められました。この級数はすべての\(x\)について収束します（レシオテスト）。この解を次数\(\nu\)の第一種ベッセル関数と呼びます。

以上、第一種ベッセル関数のガンマ関数による表示式を紹介してきました。

整数のケースでは階乗を使いましたが、ガンマ関数を使うことで関係性が一般化できて便利ですね。

木村すらいむ（@kimu3_slime）でした。ではでは。