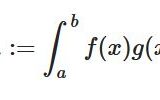どうも、木村(@kimu3_slime)です。
今回は、1次元ラプラシアンの固有値問題の解き方、固有関数とは何かを紹介します。
前提知識:偏微分方程式とは:2階線形の重要な例(ラプラス、熱、波動)
一般に、\(U \subset \mathbb{R}^N\)を領域(連結な開集合)、\(\partial U\)をその境界として、
\[ \begin{aligned}-\Delta u = \lambda u\quad x \in U \\ u=0 \quad x \in \partial U\end{aligned} \]
を満たす複素数\(\lambda\)、関数\(u(x)\)を求めよという問題を、ラプラシアン(ラプラス作用素\(-\Delta\))の固有値問題(eigenvalue problem)と呼びます。その解\(u\)は、固有関数(eigenfunction)と呼ばれます。特にディリクレ境界条件を考えているので、ディリクレ固有値(Dirichlet eigenvalue)とも。
この方程式はヘルムホルツの方程式(Helmholtz equation)とも呼ばれ、熱方程式や波動方程式を変数分離によって解く時に表れる形です。
特に今回は1次元の固有値問題を考えましょう。ラプラシアンは単に2回微分となるので、
\[ \begin{aligned}-\frac{d^2 u}{dx^2} = \lambda u\quad x \in [0,L] \\ u=0 \quad x =0,L\end{aligned} \]
という問題を解きましょう。
これは2階線形微分方程式なので、特性方程式によって解くことができます。
参考:同次形の2階線形微分方程式の解き方、学ぶ意味:熱方程式への応用を例に
特性方程式\(-\alpha^2 =\lambda\)の解は\(\alpha=\pm \sqrt{\lambda} i\)なので、解は三角関数
\[ \begin{aligned}u(x)=C_1 \cos \sqrt{\lambda} x +C_2 \sin \sqrt{\lambda} x\end{aligned} \]
です。境界条件\(u(0)=0\)から、\(C_1 =0\)となります。
今回は固有値問題を考えているので、\(u=0\)という自明解でない解を探そうとしています。したがって、境界条件\(u(L)=0\)から、
\[ \begin{aligned}C_2 \sin \sqrt{\lambda} L =0\end{aligned} \]
ですが、\(C_2 \neq 0\)となるものを求めます(\(C_1=C_2=0\)だと自明解になるので)。つまり、
\[ \begin{aligned}\sin \sqrt{\lambda}L=0\end{aligned} \]
を解きます。それは、\(\sqrt{\lambda}L = n\pi\)を満たす整数\(n\)が存在する時です。これを解けば、固有値は\(\lambda = (\frac{n \pi}{L})^2\)となりました。関数空間は一般に無限次元であるのに対応して、固有値が可算無限個ありますね。
対応する固有関数は
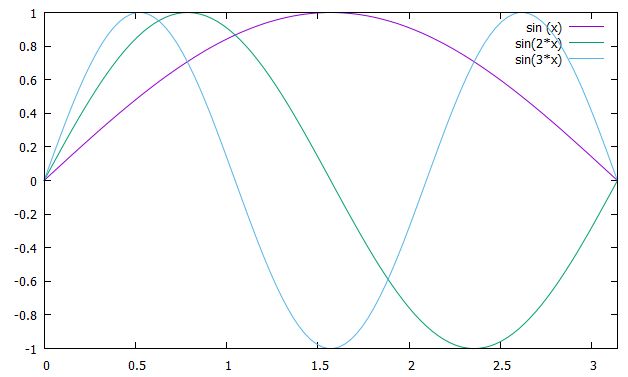
\[ \begin{aligned}u_n(x) = \sin (\frac{n\pi x}{L})\end{aligned} \]
です。三角関数系がラプラシアンの固有関数となっているわけですね。
ラプラシアン\(- \Delta\)の性質は、対称な楕円型作用素\(L\)として、次のように一般化できることが知られています。
\(L\)の固有値はすべて実数。
その固有値は可算無限個(離散的固有値)で、\((\lambda _k)\)と有限の重複を許して書くとき、
\[ \begin{aligned}0< \lambda _1 \leq \lambda_2 \leq \lambda_3 \cdots\end{aligned} \]
\[ \begin{aligned}\lim_{k\to \infty} \lambda _k = \infty\end{aligned} \]
を満たす。
さらに、対応する固有関数系\((w_k)\)は、2乗可積分な関数のなす空間\(L^2(U)\)において、完全正規直交系となるよう選べる。
また、最小の固有値\(\lambda_1>0\)は、\(L\)の主固有値(principal eigenvalue)と呼ばれ、次の性質を満たす。
\[ \begin{aligned}\lambda_1 = \min_{u \in H_0 ^1 (U),u \neq 0}\frac{B[u,u]}{\|u\|_{L^2}^2}\end{aligned} \]
\(\lambda_1\)は単純固有値(幾何学的重複度が1。\(\lambda_1\)に対応する固有関数は、定数倍の違いしかない)。
対応する固有関数\(w_1\)は、内部\(U\)において正値である。
証明については、Evans「Partial Differential Equations」を参照してください。
今回のケースと見比べてみましょう。
固有値は\(\lambda_{n}=(\frac{n \pi}{L})^2 \)なので、すべて実数、かつ可算無限個です。かつ、番号が増せば、単調に増加し無限大へ発散します。対称行列の固有値は実数で、有限個、という線形代数の結果の一般化になっています。
固有関数系\(u_n(x) = \sin (\frac{n\pi x}{L})\)は、三角関数系であり、それらは(\(L^2\)の)正規直交基底です。これはフーリエ級数展開の原理です。フーリエ級数展開ができるのは、ラプラシアンの固有関数が直交し、関数空間の基底となっているからという見方ができます。
主固有値は\(\lambda_1 = (\frac{ \pi}{L})^2\)です。
ラプラシアン(楕円型作用素)の最小固有値の性質は、線形代数におけるレイリー商による固有値の特徴づけと同様の結果が得られています。
\[ \begin{aligned} \lambda_{\min} &= \min _{x \neq 0}\frac{\langle x, Ax\rangle }{\|x\|^2} \\ &= \min _{\|x\|=1}\langle x, Ax\rangle \end{aligned} \]
主固有値に対応する固有関数は\(u_1 = \sin (\frac{\pi x}{L})\)であり、確かに内部\((0,L)\)において正値を取っているのがわかりますね。\(u_2\)以降はその正値性も崩れているのがわかります。
以上、1次元ラプラシアンの固有値問題の解き方、固有関数とは何かを紹介してきました。
フーリエ級数に関連する重要な結果でありながら、楕円型作用素として次元によらず同様の結果が一般に導けるのは面白いですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
Partial Differential Equations (Graduate Studies in Mathematics)
Amer Mathematical Society (2010-04-02T00:00:01Z)
¥9,531 (中古品)
こちらもおすすめ
熱方程式の解き方:変数分離法、フーリエ級数展開(1次元、有界領域)
線形代数の応用:関数の「空間・基底・内積」を使ったフーリエ級数展開