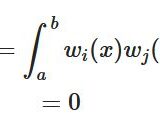関数の重み付き内積とは：内積の定義を満たすことの証明

どうも、木村（@kimu3_slime）です。

今回は、重み付き内積とは何か、それが内積の定義を満たすことの証明を紹介します。

関数の標準的な内積（\(L^2\)内積）は、

\[ \begin{aligned}\langle f,g\rangle_{L^2}:=\int _a ^b f(x)g(x)dx\end{aligned} \]

と定義されます。これに対し、正値の関数\(r(x)>0\)を使って、

\[ \begin{aligned}\langle f,g\rangle_{L^2,r}:=\int _a ^b f(x)g(x) r(x)dx\end{aligned} \]

と定義される内積を、重み付き内積（weighted inner product）と呼び、\(r(x)\)を重み関数（weight function）と呼びます。

標準的な内積は、\(r=1\)のケースとして見ることができますね。三角関数系は、重み関数\(r=1\)による重み付き内積について、直交しています。

参考：三角関数の直交性とは：フーリエ級数展開と関数空間の内積

重み付き内積から導かれるノルム

\[ \begin{aligned}\|f\|_{L^2,r}:=\sqrt{\langle f,g\rangle_{L^2,r}}\\ = \sqrt{\int _a ^b (f(x))^2 r(x)dx}\end{aligned} \]

は、重み付きノルム（weighted norm）と呼ばれます。

重み付き内積を考える動機のひとつには、ストゥルム・リウビル型方程式と呼ばれる微分方程式があります。

\[ \begin{aligned}\frac{d}{dx}(p(x) \frac{dw}{dx}(x)) + \{q(x)+ \lambda r(x)\}w(x) =0\end{aligned} \]

その方程式の異なる固有値に対応する解（固有関数）は、重み付き内積について直交していることが知られています（ストゥルム・リウビルの理論）。

例えば、三角関数系（フーリエ級数）や、ルジャンドル多項式はそこから導かれた結果のひとつと言えます。別の例として、ベッセルの微分方程式

\[ \begin{aligned}x^2 y^{\prime \prime}+xy^{\prime} +(x^2-n^2)y =0\end{aligned} \]

の解も、ストゥルム・リウビル型微分方程式であり、解の直交性が言えます。計算は略しますが、変数変換によって

\[ \begin{aligned}(xJ_n^{\prime}(kx))^{\prime} + (-\frac{n^2}{x}+ \lambda x)J_n(kx) =0\end{aligned} \]

という形になります。これは\(p(x)=x\)、\(q(x)= -\frac{n^2}{x}\)、\(r(x)=x\)のケースであり、重み\(r(x)=x\)についての直交性が導けるわけですね（積分範囲として正の値の範囲を考えることに注意）。

では、重み付き内積

\[ \begin{aligned}\langle f,g\rangle_{L^2,r}:=\int _a ^b f(x)g(x) r(x)dx\end{aligned} \]

が（抽象）内積の定義

\(V\)を線形空間とする。2変数関数\(\langle \cdot,\cdot \rangle :V\times V \to \mathbb{R}\)は、次を満たすとき内積と呼ばれる。

任意の\(a,b\in V\)、\(\lambda \in \mathbb{R}\)に対し、

(1) 対称性：\(\langle a,b\rangle =\langle b,a\rangle\)

(2) （二重）線形性：\(\langle \lambda a+c,b\rangle = \lambda \langle a,b\rangle +\langle c,b\rangle\)

(3) 正定値性：\(\langle a,a\rangle \geq 0\)。\(a\neq 0\)ならば\(\langle a,a\rangle > 0\)。

を満たすことを確かめましょう。

線形空間としては、内積が定義される関数空間\(V=L^2([a,b])\)を考えています。\(f,g ,h\in V\)、\(\lambda\)をスカラーとします。

関数の値、数の積の可換性により、

\[ \begin{aligned} \langle f,g\rangle_{L^2,r}&=\int _a ^b f(x)g(x) r(x)dx \\ &= \int _a ^b g(x)f(x) r(x)dx \\ &= \langle g,f\rangle_{L^2,r}\end{aligned} \]

なので、対称性を満たします。

積分の線形性より、

\[ \begin{aligned} \langle \lambda f+h,g\rangle_{L^2,r}&=\int _a ^b (\lambda f(x)+h(x))g(x) r(x)dx \\ &= \lambda\int _a ^b f(x)g(x) r(x)dx +\int _a ^b h(x)g(x) r(x)dx \\ &= \langle f,g\rangle_{L^2,r}+\langle h,g\rangle_{L^2,r}\end{aligned} \]

なので、線形性を満たします。

まず、仮定より常に\((f(x))^2 r(x) \geq 0\)です。したがって、積分の単調性より、

\[ \begin{aligned} \langle \lambda f,f\rangle_{L^2,r}&=\int _a ^b (f(x))^2 r(x)dx \\ & \geq \int_a ^b 0dx\\&= 0\end{aligned} \]

です。\(f \neq 0\)のときは、仮定より\((f(x))^2 r(x) > 0\)となる一定の範囲が存在します。再び単調性により

\[ \begin{aligned} \langle \lambda f,f\rangle_{L^2,r}&=\int _a ^b (f(x))^2 r(x)dx \\ &>&0\end{aligned} \]

となり、正値性が言えました。よって、重み付き内積は内積の定義を満たすことがわかりました。

ベクトルの内積としても、\(r=(r_1,\dots,r_k)\)をその成分がすべて正のベクトル（定数）として

\[ \begin{aligned}\langle x,y\rangle_{r}:= \sum_{k=1}^N x_k y_k r_k\end{aligned} \]

という重み付き内積を考えることができます。例えば

\[ \begin{aligned}\langle x,y\rangle= x_1y_1+2 x_2y_2\end{aligned} \]

も内積の定義を満たします。証明は上で行ったものと同様です。

一貫して\(r\)は正であるという仮定がありましたが、これは内積の正定値性の保証のために必要です。例えば\(r=-1\)としたら、