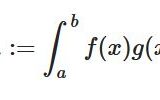ストゥルム・リウビル型微分方程式における固有関数の直交性の証明

どうも、木村（@kimu3_slime）です。

今回は、ストゥルム・リウビル型微分方程式における、固有関数の直交性の証明を紹介します。

ストゥルム・リウビル型の微分方程式とは、

\[ \begin{aligned}\frac{d}{dx}(p(x) \frac{dw}{dx}(x)) + \{q(x)+ \lambda r(x)\}w(x) =0\end{aligned} \]

\[ \begin{aligned}\alpha_1 w(a)+ \alpha_2 \frac{dw}{dx}(a)=0\end{aligned} \]

\[ \begin{aligned}\beta_1 w(b)+ \beta_2 \frac{dw}{dx}(b)=0\end{aligned} \]

と表される\(w\)に関する常微分方程式です。

ここで、変数\(x\)は\(\mathbb{R}\)の有界な閉区間\([a,b]\)上で動き、\(p,q,r\)は連続関数で\(p(x)>0,r(x)>0\)を満たし、\(\lambda,\alpha_1,\alpha_2,\beta_1,\beta_2\)は定数で、\(\alpha_1,\alpha_2\)、\(\beta_1,\beta_2\)の一方は0でないとします。

\(\lambda\)をパラメータと考え、その\(\lambda\)に対して方程式に非自明な解\(w\)が存在するとき、その\(\lambda\)を固有値、対応する解\(w\)を固有関数と呼びます。

参考：ストゥルム・リウビル型微分方程式の発見：熱方程式から

その固有値は可算無限個であることが知られています。それらを\((\lambda_n)\)と番号付けましょう。対応する固有関数を\((w_n)\)とします。

異なる固有値に対応する固有関数\(w_i,w_j\)が、重み付き内積について直交すること

\[ \begin{aligned}\langle w_i,w_j\rangle_{L^2,r}:=\int _a ^b w_i(x)w_j(x) r(x)dx\\ =0\end{aligned} \]

を証明しましょう。

参考：関数の重み付き内積とは：内積の定義を満たすことの証明

まず、固有関数が方程式を満たすので、

\[ \begin{aligned}(p(x) w_i ^{\prime}(x))^\prime + \{q(x)+ \lambda_i r(x)\}w_i(x) =0\end{aligned} \]

\[ \begin{aligned}(p(x) w_j ^{\prime}(x))^\prime + \{q(x)+ \lambda_j r(x)\}w_j(x) =0\end{aligned} \]

となります。上の式に\(w_j\)、下の式に\(w_j\)をかけて差を取りましょう。\(q\)がかかる項はキャンセルされ、

\[ \begin{aligned}(p(x) w_i ^{\prime}(x))^\prime w_j -(p(x) w_j ^{\prime}(x))^\prime w_i \\+(\lambda_i-\lambda_j)r(x)w_i w_j=0\end{aligned} \]

です。右側に目標となる形が現れました。それを移項し、両辺を積分して、部分積分で計算すると、

\[ \begin{aligned} & -(\lambda_i-\lambda_j) \int_a^b w_i w_j r(x)dx \\ &=\int_a^b(p(x) w_i ^{\prime}(x))^\prime w_j -(p(x) w_j ^{\prime}(x))^\prime w_i dx \\ &= [p(x) w_i ^{\prime}(x) w_j]_a^b -p(x) w_i ^{\prime}(x) w_j^{\prime}\\ & -[p(x) w_j ^{\prime}(x) w_i]_a^b +p(x) w_i ^{\prime}(x) w_j^{\prime} \\ &=[p(x) (w_i ^{\prime}w_j-w_j ^{\prime} w_i)]_a^b\end{aligned} \]

となります。異なる固有値を考えているので、\(\lambda_i-\lambda_j \neq 0\)です。したがって、右辺の値が0であるならば、結論が示せます。

そこで境界条件

\[ \begin{aligned}\alpha_1 w_i(a)+ \alpha_2 w_i ^{\prime}(a)=0\end{aligned} \]

\[ \begin{aligned}\alpha_1 w_j(a)+ \alpha_2 w_j ^{\prime}(a)=0\end{aligned} \]

を利用しましょう。上の式に\(w_j\)、下の式に\(w_i\)をかけて差を取れば、

\[ \begin{aligned}\alpha_2 (w_i ^{\prime}(a) w_j(a)- w_j ^{\prime}(a) w_i(a))=0\end{aligned} \]

となります。仮定より\(\alpha_1,\alpha _2\)のどちらか一方は0ではありません。\(\alpha_2 \neq 0\)のときは、かっこの中身が0となります。\(\alpha_2 =0\)のときは、\(\alpha_1 \neq 0\)、境界条件から\(w_i (a)=w_j(a)=0\)です。

全く同様にして、もうひとつの境界条件

\[ \begin{aligned}\beta_1 w_i(b)+ \beta_2 w_i ^{\prime}(b)=0\end{aligned} \]

\[ \begin{aligned}\beta_1 w_j(b)+ \beta_2 w_j ^{\prime}(b)=0\end{aligned} \]

から、

\[ \begin{aligned} w_i ^{\prime}(b) w_j(b)- w_j ^{\prime}(b) w_i(b))=0\end{aligned} \]

または\(w_i (b)=w_j(b)=0\)が得られます。

よって、いずれのケースであっても、

\[ \begin{aligned} & \int_a^b w_i w_j r(x)dx \\ &= -\frac{1}{(\lambda_i – \lambda_j)}[p(x) (w_i ^{\prime}w_j-w_j ^{\prime} w_i)]_a^b\\&=0\end{aligned} \]

となり、異なる固有値に対応する固有関数の直交性がわかりました。

以上、ストゥルム・リウビル型微分方程式における、固有関数の直交性の証明を紹介してきました。

三角関数、ルジャンドル多項式、ベッセル関数といった関数系の直交性がすべてここから導けます。ぜひストゥルム・リウビル型微分方程式の一般的で便利な性質を利用してみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。