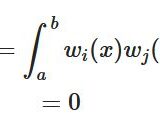フーリエ係数に関するオイラーの公式の導出

どうも、木村（@kimu3_slime）です。

今回は、フーリエ係数に関するオイラーの公式とは何か、その導出を紹介します。

フーリエ級数に関するオイラーの公式
オイラーの公式の導出
一般的な周期\(2L\)のオイラーの公式
こちらもおすすめ

フーリエ級数に関するオイラーの公式

区間\([-\pi,\pi]\)において周期的な関数\(f\)のフーリエ級数展開を

\[ \begin{aligned}f(x)=a_0 + \sum_{n=1}^\infty (a_n \cos nx +b_n \sin nx)\end{aligned} \]

としましょう。そのフーリエ係数は関数\(f\)によって決定され、

\[ \begin{aligned}a_0=\frac{1}{2\pi} \int_{-\pi}^{\pi} f(x)dx\end{aligned} \]

\[ \begin{aligned}a_n=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x)\cos nxdx\end{aligned} \]

\[ \begin{aligned}b_n=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x)\sin nx dx\end{aligned} \]

と表されます。これはフーリエ係数に関するオイラーの公式（Euler’s formula）と呼ばれるものです。複素指数関数に関するオイラーの公式とは別物なので注意。

\(a_0\)についてはもうひとつの表記法があり、

\[ \begin{aligned}f(x)=\frac{a_0}{2} + \sum_{n=1}^\infty (a_n \cos nx +b_n \sin nx)\end{aligned} \]

とあらかじめ\(1/2\)を組み込んでおくことで、

\[ \begin{aligned}a_n=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x)\cos nxdx\end{aligned} \]

を\(n=0\)のケースで成り立つ式として捉えることができます。

オイラーの公式の導出

では、フーリエ係数に関するオイラーの公式を導出していきましょう。

重要なのは、三角関数系\(\{1 ,\cos nx, \sin nx\}_{n=1}^\infty\)が、積分によって定まる内積について直交していることです。

\langle \cos kx , \cos \ell x\rangle&= \int _{-\pi}^{\pi} \cos kx \cos \ell x dx\\ &= 0 \

\langle \sin kx , \sin \ell x\rangle&= \int _{-\pi}^{\pi} \sin kx \sin \ell x dx\\ \\ &= 0 \

\langle \cos kx , \sin \ell x\rangle&= \int _{-\pi}^{\pi} \cos kx \sin \ell x dx\\&= 0 \

これらは計算して確かめられますが、直交性は基本的で覚えて良い結果だと思います。

参考：三角関数の直交性とは：フーリエ級数展開と関数空間の内積

フーリエ級数展開

\[ \begin{aligned}f(x)=a_0 + \sum_{n=1}^\infty (a_n \cos nx +b_n \sin nx)\end{aligned} \]

において、\(\{1 ,\cos nx, \sin nx\}_{n=1}^\infty\)のいずれかひとつとの内積を取ることで、係数を求めてみましょう。

まずは定数関数\(1\)との内積を取ると、内積の線形性から和や積と積分の順序を交換できて、

\[ \begin{aligned} &\int_{-\pi}^\pi f(x)dx \\&= \langle f,1\rangle \\ &= \langle a_0 + \sum_{n=1}^\infty (a_n \cos nx +b_n \sin nx) ,1\rangle\\ &=\langle a_0,1\rangle +\sum_{n=1}^\infty (a_n\langle \cos nx,1\rangle+b_n\langle \sin nx,1\rangle)\\ &= \langle a_0,1\rangle \\&= a_0 \int _{-\pi }^{\pi} 1dx \\&= 2\pi a_0 \end{aligned} \]

となるので、

\[ \begin{aligned}a_0 = \frac{1}{2\pi}\int_{-\pi}^\pi f(x)dx \end{aligned} \]

がわかりました。内積を取った関数の成分以外はすべて直交しているので、結果として\(f\)の定数関数の成分\(a_0\)だけが取り出されます。

続いて、\(\cos kx\)との内積を取りましょう（級数の添字\(n\)と\(k\)が混ざらないように注意）。

\[ \begin{aligned} &\int_{-\pi}^\pi f(x) \cos kx dx \\&= \langle f,\cos kx\rangle \\ &= \langle a_0 + \sum_{n=1}^\infty (a_n \cos nx +b_n \sin nx) ,\cos kx\rangle\\ &=\langle a_0,\cos kx \rangle +\sum_{n=1}^\infty (a_n\langle \cos nx,\cos kx\rangle+b_n\langle \sin nx,\cos kx\rangle)\\ &= a_k \langle \cos kx ,\cos kx\rangle\\ &= a_k \int _{-\pi }^{\pi} (\cos kx)^2dx \\&= \frac{a_k}{2}\int _{-\pi}^{\pi} (\cos 2k x +1) dx \\ &= \frac{a_k}{2}[\frac{1}{2k}\sin 2kx +x]_{-\pi} ^\pi\\ &= a_k\pi\end{aligned} \]

なので、

\[ \begin{aligned}a_n = \frac{1}{\pi}\int_{-\pi}^\pi f(x) \cos nx dx \end{aligned} \]

となります。

再び同様にして、\(\sin kx\)との内積を取ると

\[ \begin{aligned} &\int_{-\pi}^\pi f(x) \sin kx dx \\&= \langle f,\sin kx\rangle \\ &= \langle a_0 + \sum_{n=1}^\infty (a_n \cos nx +b_n \sin nx) ,\sin kx\rangle\\ &=\langle a_0,\sin kx \rangle +\sum_{n=1}^\infty (a_n\langle \cos nx,\sin kx\rangle+b_n\langle \sin nx,\sin kx\rangle)\\ &= a_k \langle \sin kx ,\sin kx\rangle\\ &= b_k \int _{-\pi }^{\pi} (\sin kx)^2dx \\&= \frac{b_k}{2}\int _{-\pi}^{\pi} (-\cos 2k x +1) dx \\ &= \frac{b_k}{2}[-\frac{1}{2k}\sin 2kx +x]_{-\pi} ^\pi\\ &= b_k\pi\end{aligned} \]

なので、

\[ \begin{aligned}b_n = \frac{1}{\pi}\int_{-\pi}^\pi f(x) \sin nx dx \end{aligned} \]

となりました。

内積を取る時、最後の計算で\(2\pi ,\pi\)といった係数が出てくるのは、少し面倒です。これを考慮して、正規化した三角関数系\(\frac{1}{2\pi}, \frac{1}{\pi} \cos nx , \frac{1}{\pi}\sin nx\)を考えることもあるでしょう。これらを使えば、

\[ \begin{aligned}\langle f, \frac{1}{2\pi}\rangle =a_0\end{aligned} \]

\[ \begin{aligned}\langle f, \frac{1}{\pi} \cos n x \rangle= a_n\end{aligned} \]

\[ \begin{aligned}\langle f, \frac{1}{\pi} \sin nx \rangle= b_n\end{aligned} \]

といったシンプルな表示式が得られます。結果は全く同じですが。