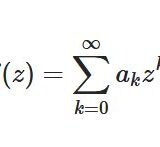どうも、木村(@kimu3_slime)です。
前回、複素指数関数、三角関数のべき級数による定義を紹介しました。
今回は、複素解析におけるオイラーの公式、指数・三角関数の性質を紹介します。
オイラーの公式
オイラーの公式(Euler’s formula)とは、複素指数関数・三角関数の関係を表す等式です。
\[ \begin{aligned}e^{iz}= \cos z + i \sin z\end{aligned} \]
これをラフに証明しましょう。それぞれはべき級数で定義された関数でした。
\[ \begin{aligned}e^z := \sum_{k=0} ^\infty \frac{1}{k!}z^k\end{aligned} \]
\[ \begin{aligned}\sin z := \sum_{k=0} ^\infty \frac{(-1)^k}{(2k+1)!}z^{2k+1}\end{aligned} \]
\[ \begin{aligned}\cos z := \sum_{k=0} ^\infty \frac{(-1)^k}{(2k)!}z^{2k}\end{aligned} \]
さて、ここで\(e^z\)の右辺で\(z\)を\(iz\)に置き換えてみます。\(i^2=-1\)に気をつけると、最初の方の項は
\[ \begin{aligned}1+zi+\frac{-1}{2!}z^2+\frac{-1}{3!}z^3 i+\frac{1}{4!} z^4 +\cdots \\ = (1-\frac{1}{2!} z^2 + \frac{1}{4!} z^4+ \cdots )+ i (z +\frac{-1}{3!} z^3+ \cdots)\end{aligned} \]
です。つまり、偶数番と奇数番の項の2つに分けることができます。第\(n\)項までの有限和を取りましょう。\(n=2m\)のとき、
\[ \begin{aligned}\sum _{k=0} ^n \frac{1}{k!}{(zi)}^k=\sum_{k=0}^{m} \frac{(-1)^k}{(2k)!} z^{2k} + i(\sum_{k=0} ^{m-1} \frac{(-1)^k}{(2k+1)!}z^{2k+1})\end{aligned} \]
となります。右辺の前半が\(\cos z\)、後半が\( i\sin z\)に対応しそうです。ここで\(n \to \infty\)と極限を取りたいのですが、注意すべきことがあります。
級数を2つの部分に並べ替えていますが、一般に級数は、並べ替えると極限値が変わってしまう可能性があるのです。しかし、級数が絶対収束しているならば、それは起こり得ないことが知られています。(収束するが絶対収束しない級数、並び替えによって値が変わりうる級数は条件収束すると呼ばれます。詳しくは、杉浦「解析入門 Ⅰ」p.45などを参照。)
複素指数関数、三角関数を定義するべき級数は、すべての複素数\(z \in \mathbb{C}\)について絶対収束しています。そこで、さきほどの等式で問題なく極限を取ることができて、
\[ \begin{aligned} e^{iz} &= \lim_{n\to \infty }\sum _{k=0} ^n \frac{1}{k!}{(zi)}^k \\ &= \lim_{m \to \infty}\sum_{k=0}^{m} \frac{(-1)^k}{(2k)!} z^{2k} + \lim_{m \to \infty} i(\sum_{k=0} ^{m-1} \frac{(-1)^k}{(2k+1)!}z^{2k+1}) \\ &= \cos z +i \sin z\end{aligned} \]
が得られました。
オイラーの公式はすべての複素数\(z\)について成り立つものですが、特に\(z=\theta \)を実数としたケースがよく使われます。
\[ \begin{aligned}e^{i\theta}= \cos \theta + i \sin \theta\end{aligned} \]
一般の複素数\(z =x+iy\)は、複素数平面において原点からの距離を\(r\)、実軸の正の部分から測った角度を\(\theta \)とすると、
\[ \begin{aligned} z &=x+ iy \\ &=r \cos \theta + i r \sin \theta \\ &= re^{i\theta} \ \end{aligned} \]
と表せます。
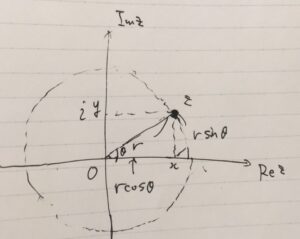
このような表示を\(z\)の極形式(polar form)と言いますが、これをシンプルに\(z= r e^{i \theta}\)と表せるのがオイラーの公式のメリットのひとつです。\(e^{i \theta}\)が複素平面乗の半径1の円周上の点であり、角度\(\theta\)を動かせば円周ができあがります。このように幾何学的に捉えるのが大事です。
オイラーの公式は複素指数関数を2つの三角関数に分けるものですが、実指数関数も2つの関数に分けて表すことができます。
\[ \begin{aligned} e^x &= \frac{e^x +e^{-x}}{2} +\frac{e^x-e^{-x}}{2}\\&= \cosh x + \sinh x \end{aligned} \]
これらは双曲線関数と呼ばれるもので、三角関数と似た性質を持っています。\(\cos, \cosh\)は偶関数で、\(\sin ,\sinh\)は奇関数であり、オイラーの公式は指数関数の偶関数成分、奇関数成分を取り出した式と見れますね。
また、オイラーの公式は三角関数\(\sin ,\cos\)を指数関数\(e^{z}\)にひとまとめるにするものなので、三角関数による級数展開を考えるフーリエ級数の理論、「波」に関する学問で幅広く応用されています。
参考:線形代数の応用:関数の「空間・基底・内積」を使ったフーリエ級数展開
複素指数関数、三角関数の性質
他にも、複素指数関数、三角関数には次のような性質が成り立つことが知られています。
指数法則:\(e^{z+w}= e^z e^w\)
周期性:\(e^{z} =e^{w}\)であることと、ある整数\(k\)により\(z= w+ 2\pi k i\)と表されることは同値。
\[ \begin{aligned}\cos (z+ 2\pi)= \cos z ,\sin (z+2\pi )=\sin z \end{aligned} \]
\[ \begin{aligned}(\cos z)^2+(\sin z)^2 =1\end{aligned} \]
\[ \begin{aligned}\frac{d}{dz} e^z = e^z\end{aligned} \]
\[ \begin{aligned}\frac{d}{dz} \cos z = -\sin z , \frac{d}{dz} \sin z = \cos z\end{aligned} \]
指数法則とオイラーの公式からは、ド・モアブルの定理(de Moivre’s theorem)が導かれます。
\[ \begin{aligned} e^{i \theta k}= (e^{i\theta}) ^k\end{aligned} \]
\[ \begin{aligned}\cos k\theta + i \sin k \theta = (\cos \theta + i \sin \theta )^k\end{aligned} \]
両辺の実部、虚部を比較すると、三角関数の\(k\)倍角の公式を導くことができて、便利です。指数関数の指数法則とオイラーの公式は、三角関数の加法定理を導く一般的な性質だった、というわけですね。
複素指数関数が周期性\(e^z = e^{z+2 \pi k i}\)を持つのは、実関数と違って、意外に思うかもしれません。しかしオイラーの公式によれば、\(z= x+iy\)に対し、
\[ \begin{aligned} e^z &=e^{x+iy} \\ &=e^{x}e^{iy} \\&=e^x(\cos y + i \sin y) \end{aligned} \]
が成り立つので、虚部\(y\)が\(2\pi\)の整数倍だけずれても同じ値になります。実三角関数の持つ周期性によって、複素指数関数は必然的に周期性を持つわけですね。
以上、オイラーの公式、複素指数関数・三角関数の性質を紹介してきました。
オイラーの公式は「美しい定理」と評されることがあります。おそらく、シンプルでわかりやすく、複素数の理論を知らないと不思議な式に見えるのでしょう。が、指数・三角関数のべき級数表示と虚数の関係を見比べれば、当たり前の性質とも言えます。
あまり神秘的に受け止めすぎず、三角関数の公式と同様に、オイラーの公式を当然のものとして使って、複素数の世界に馴染んでみてはいかがでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (2003-12-12T00:00:01Z)
¥2,640
Complex Analysis (Graduate Texts in Mathematics (103))
Springer (1999-01-15T00:00:01Z)
¥9,011
東京大学出版会 (1980-03-31T00:00:01Z)
¥3,080