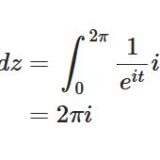複素微分、正則関数・解析関数とは：具体例をもとに

どうも、木村（@kimu3_slime）です。

今回は、複素関数の微分、正則関数・解析関数、コーシー・リーマンの方程式とは何か、具体例をもとに紹介します。

複素微分の驚き：正則関数と解析関数
コーシー・リーマンの方程式
こちらもおすすめ

複素微分の驚き：正則関数と解析関数

複素関数の微分は、実関数の微分と良く似ているように見えるのですが、実は全くの別物であることが、今回伝えたいことです。

まずは定義から確認していきましょう。\(\mathbb{C}\)を複素数全体の集合とします。複素関数\(f : \mathbb{C}\to \mathbb{C}\)が微分可能であるとは、

\[ \begin{aligned}\lim_{h\to 0} \frac{f(z+h)-f(z)}{h}\end{aligned} \]

という極限が存在することで、存在するときはそれを\(f^{\prime}(z)\)や\(\frac{df}{dz}(z)\)と書きます。

この定義によると、べき乗関数の微分は\(\frac{d}{dz}(z^{k})=z^{k-1}\)と期待した通りになります。また、指数関数\(\frac{d}{dz} e^z = e^z\)や、三角関数\(\frac{d}{dz} \cos z = -\sin z\) , \(\frac{d}{dz} \sin z = \cos z\)といった、実関数と同様の微分法則が成り立つのです。べき級数で定義される関数も、その収束円盤内で項別微分ができます。

ただし、対数関数や一般のべきには注意が必要です。（これについては別記事にて）

参考：複素べき級数、収束半径とは：指数・三角関数を例に

また、微分可能な関数の和、スカラー倍、積もまた微分可能であり、線形性を持っています。積の微分法則、合成関数の微分法則（チェインルール）も成り立ちます。

参考：連続関数、可積分関数のなす線形空間、微分と積分の線形性とは

さて複素微分特有の性質は、1回微分できる関数は必ず何回でも微分できる、ということです。

実関数については、1回微分可能であることと、何回でも微分できること（無限回微分可能）は全くの別物です。

\[ \begin{aligned}f(x)= \begin{cases}-x^2 & (x <0 )\\x^2 & (x\geq 0)\end{cases}\end{aligned} \]

例えば上の関数は、1回微分可能（\(C^{1}\)級）ですが、導関数は\(2|x|\)になり、\(x=0\)において2回微分不可能（\(C^{2}\)級でない）です。

参考：関数のなめらかさと微分可能性 C^k級関数とは

複素微分可能な関数では、このような現象が起こりえません。「無限回微分可能ならば1回微分可能」で逆は一般に成り立たないのが実微分の理論ですが、複素微分では逆が成り立つのです。

そこで、\(f\)の定義域\(D\)の各点で複素微分可能な関数には、正則関数（holomorphic function, regular function）という特別な呼び名があります。多項式関数、指数関数、三角関数といった初等関数は正則関数ですし、\(\frac{1}{z}\)は\(z \neq 0\)で正則です。

さらには、正則関数はその各点でべき級数に展開することができます。

\(f\)を\(z=z_0\)を含む円盤\(D(z_0,R):=\{z \in \mathbb{C} \mid |z-z_0| <R\}\)で正則な関数とすると、\(z \in D(z_0,R)\)において

\[ \begin{aligned}f(z) = \sum_{k=0} ^\infty \frac{f^{k} (z_0) }{k!} (z-z_0)^k\end{aligned} \]

とテイラー展開できる。これはコーシーの積分公式と呼ばれる結果により導かれるものです。（別記事にて紹介予定）

べき級数に展開できる関数は一般に、解析関数（analytic function）と呼ばれます。

実関数については、1回微分可能、無限回微分可能であるからといって、解析関数であるとは限りません。

しかし複素関数については、正則関数であること（1回微分可能であること、無限回微分可能）と、解析関数であること（べき級数に展開できる）は同値になるのです。これは驚くべき結果と言えないでしょうか。

コーシー・リーマンの方程式

どうして複素微分では、実関数では考えられないような「強い」結果が得られるのでしょうか。

そもそも、一見普通に見える複素微分の定義で、極限

\[ \begin{aligned}\lim_{h\to 0} \frac{f(z+h)-f(z)}{h}\end{aligned} \]

が存在するということは、複素平面上のあらゆる方向から\(h\)が\(0\)に近づいたときの値が一致する、ということです。

これは実関数の偏微分可能性（1つの方向による微分）ではなく、全微分可能性（あらゆる方向に対する微分係数の存在）を意味しているのと同じです。

参考：2変数関数と偏微分：グラフ、接平面を描いてみよう

つまり、複素微分可能性、正則性を課した時点で、関数は強い制限がかかっているわけです。

例えば、\(z=x+iy\)と実部虚部を表すとき、複素共役を取る関数\(f(z) =\overline{z}=x-iy\)は正則ではありません。

\(h = re^{i\theta}\)と極形式で表し、極限を考えてみましょう。オイラーの公式\(e^{i\theta} =\cos \theta + i \sin \theta\)より、\(\overline{h}=re^{-i\theta}\)なので、

\[ \begin{aligned}\lim_{h\to 0} \frac{\overline{z+h}-\overline{z}}{h}=\frac{re^{-i\theta}}{re^{i\theta}}=e^{-2i\theta}\end{aligned} \]

となります。例えば\(\theta= 0, \frac{-\pi}{4}\)といった異なる角度から\(r \to 0\)とすると、\(h \to 0\)になりますが、その極限値は異なる（\(1,i\)）ので、極限は存在しません。

複素関数の微分可能性の判定方法として、次のような言い換えが知られています。

コーシー・リーマンの方程式（Cauchy–Riemann equations）

複素関数\(f\)を、\(f(z) =u(x,y)+i v(x,y)\)と実部\(u\)、虚部\(v\)に分けて表すとする。

\(f\)が正則であることと、次の方程式を満たすことは同値。

\[ \begin{aligned}\frac{\partial u}{\partial x } (x,y)=\frac{\partial v}{\partial y}(x,y)\end{aligned} \]

\[ \begin{aligned}\frac{\partial u}{\partial y } (x,y)= -\frac{\partial v}{\partial x}(x,y)\end{aligned} \]

この結果は複素微分の定義を、実部と虚部に分けて導かれるものです。証明は神保「複素関数入門」などを参照。

例えば、\(f(z) =\overline{z}=x-iy\)について、その実部は\(u(x,y)=x\)、虚部は\(v(x,y)=-y\)です。\(\frac{\partial u}{\partial x }=1 \neq -1 =\frac{\partial v}{\partial y}\)で、コーシーリーマンの方程式を確かに満たしていませんね。

次のように言い換えることもできます。微分作用素\(\frac{\partial}{\partial \overline {z}} \)を

\[ \begin{aligned} \frac{\partial f}{\partial \overline {z}} &= \frac{1}{2} (\frac{\partial }{\partial x}+ i\frac{\partial }{\partial y})(u+iv) \\ &= \frac{1}{2}(\frac{\partial u}{\partial x } -\frac{\partial v}{\partial y})+\frac{i}{2}(\frac{\partial u}{\partial y } +\frac{\partial v}{\partial x}) \end{aligned} \]

と定めましょう（ヴィルティンガー微分）。コーシー・リーマンの方程式は、

\[ \begin{aligned} \frac{\partial f}{\partial \overline {z}} =0\end{aligned} \]

と言い換えられます。\(f(z) = \overline {z}\)ならば、\(\frac{\partial f}{\partial \overline {z}} =1 \neq 0\)で、わかりやすいですね。

また、コーシー・リーマンの方程式からは、正則関数の実部、虚部\(u,v\)がある性質を満たすことが導かれます。方程式を偏微分すると、

\[ \begin{aligned}\frac{\partial^2 u}{\partial x^2 } (x,y)=\frac{\partial v}{\partial x \partial y }(x,y)\end{aligned} \]

\[ \begin{aligned}\frac{\partial u}{\partial y ^2 } (x,y)= -\frac{\partial v}{\partial x \partial y}(x,y)\end{aligned} \]

で、\(C^2\)級なら偏微分の順序によらずに右辺は（符号違いで）一致し、

\[ \begin{aligned}\frac{\partial^2 u}{\partial x^2 } (x,y) +\frac{\partial^2 u}{\partial y^2 } (x,y)=0\end{aligned} \]

という方程式を満たしていることがわかります（\(v\)も同様）。

この微分方程式（\(\Delta u =0\)）はラプラス方程式と呼ばれ、その解は調和関数と呼ばれます。

ラプラス方程式は熱方程式（拡散方程式）や波動方程式の定常状態として現れるもので、調和関数は必ずなめらか（\(C^{\infty}\)級）になるなど、多くの結果が知られています。

以上、複素関数の微分とは何か、正則関数、解析関数、コーシー・リーマンの方程式について、例を挙げながら紹介してきました。