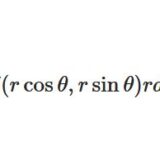どうも、木村(@kimu3_slime)です。
ベクトル解析における名前のついた定理といえば、グリーンの定理、ストークスの定理、ガウスの発散定理が有名です。
今回は、グリーンの定理を、具体例を通じて紹介していきたいと思います。
グリーンの定理とは
グリーンの定理は、平面上の閉じた曲線におけるベクトル値関数の線積分と、その曲線によって囲まれる領域における重積分が関係をもつ、という定理です。
\(D\subset \mathbb{R}^2\)を有界な領域で、その境界が\(C^1\)級の曲線をつなぎあわせた閉曲線\(c\)によって表されるとする。\(F:D\to \mathbb{R}^2\)、\(F=(F_1,F_2)\)を\(C^1\)級とする。このとき、次の式が成り立つ。
\[ \begin{aligned}\int _c F = \int _D (-\frac{\partial F_1}{\partial y}+\frac{\partial F_2}{\partial x})dxdy\end{aligned} \]
領域とは、連結な集合のことです。連結とは、おおざっぱに言えばひとまとまりにつながってることで、円盤や三角形、長方形は連結。詳しくは別記事で紹介予定。
曲線とは、連続な関数\(c:[a,b]\to \mathbb{R}^2\)のこと。閉曲線とは、始点と終点が一致した曲線\(c(a)=c(b)\)です。
左辺の線積分\(\int _c f \)において、\(c\)は領域\(D\)を左手に見るように、反時計回りにパラメータ付けされているものとしています。
例を通じてグリーンの定理を考える
と、グリーンの定理の主張を一般的に眺めてもよくわからないと思うので、簡単な具体例を通じて考えましょう。
領域としては正方形\(D=[0,1]\times [0,1]\)を考えましょう。その境界を表す閉曲線\(c\)は、次の4つの曲線をつなぎあわせたものです。\(c_1(t)=(t,0)\)、\(c_2(t)=(1,t)\)、\(c_3(t)=(1-t,1)\)、\(c_4(t)=(0,1-t)\)で、定義域は\([0,1]\)となっています。

\(F:\mathbb{R}^2 \to \mathbb{R}^2\)の例を、\(F(x,y)=(F_1(x,y),F_2(x,y))=(y,x)\)とします。
ベクトル場の線積分の定義は、\(\int _c f :=\int_a ^b \langle F(c(t)) ,c^{\prime }(t) \rangle dt\)でした。それぞれの経路における線積分を計算します。
\[ \begin{aligned}\int_{c_1} F =\int_0 ^1 \langle (0,t) ,(1,0) \rangle dt=0\end{aligned} \]
\[ \begin{aligned}\int_{c_2} F =\int_0 ^1\langle (t,1) ,(0,1) \rangle dt=1\end{aligned} \]
\[ \begin{aligned}\int_{c_3} F =\int_0 ^1\langle (1,1-t) ,(-1,0) \rangle dt=-1\end{aligned} \]
\[ \begin{aligned}\int_{c_4} F =\int_0 ^1\langle (1-t,0) ,(0,-1) \rangle dt=0\end{aligned} \]
なので、閉曲線\(c\)における線積分はこれらの和で、\(\int _c F =0\)です。
一方で、\(-\frac{\partial F_1}{\partial y}+\frac{\partial F_2}{\partial x}=-1+1=0 \)なので、
\[ \begin{aligned}\int _D (-\frac{\partial F_1}{\partial y}+\frac{\partial F_2}{\partial x})dxdy =0\end{aligned} \]
であり、グリーンの定理が成立していることがわかります。
別の例として、\(G=(G_1,G_2)=(y,-x)\)を同じ領域で積分してみましょう。
\[ \begin{aligned}\int_{c_1} G=\int_0 ^1 \langle (0,-t) ,(1,0) \rangle dt=0\end{aligned} \]
\[ \begin{aligned}\int_{c_2} G =\int_0 ^1\langle (t,-1) ,(0,1) \rangle dt=-1\end{aligned} \]
\[ \begin{aligned}\int_{c_3} G =\int_0 ^1\langle (1,-(1-t)) ,(-1,0) \rangle dt=-1\end{aligned} \]
\[ \begin{aligned}\int_{c_4} G =\int_0 ^1\langle (1-t,0) ,(0,-1) \rangle dt=0\end{aligned} \]
なので、\(\int _c G =-2\)です。
一方で、\(-\frac{\partial G_1}{\partial y}+\frac{\partial G_2}{\partial x}=-1-1=-2 \)なので、
\[ \begin{aligned}\int _D -2 dxdy =-2\end{aligned} \]
であり、グリーンの定理が成立しています。
正方形領域における証明
これら例を見ると、関数\(F=(F_1,F_2)\)が一般のものであっても、成立することが示せそうです。
\[ \begin{aligned}\int_{c_1} F =\int_0 ^1 \langle (F_1,F_2) ,(1,0) \rangle dt=\int _0^1 F_1 (c_1)dt\end{aligned} \]
\[ \begin{aligned}\int_{c_2} F =\int_0 ^1\langle (F_1,F_2) ,(0,1) \rangle dt=\int _0^1 F_2(c_2) dt\end{aligned} \]
\[ \begin{aligned}\int_{c_3} F =\int_0 ^1\langle (F_1,F_2) ,(-1,0) \rangle dt=-\int _0^1 F_1(c_3) dt\end{aligned} \]
\[ \begin{aligned}\int_{c_4} F =\int_0 ^1\langle (F_1,F_2) ,(0,-1) \rangle dt=-\int _0^1 F_2(c_4) dt\end{aligned} \]
と、それぞれの線積分はシンプルになります。重積分は逐次積分として計算でき、
\[ \begin{aligned}\int _D (-\frac{\partial F_1}{\partial y}+\frac{\partial F_2}{\partial x})dxdy = \int _0^1 \int _0 ^1 (-\frac{\partial F_1}{\partial y}+\frac{\partial F_2}{\partial x})dxdy\end{aligned} \]
ですが、これを微積分学の基本定理を使って整理しましょう。まず\(y\)に注目することで、
\[ \begin{aligned} \int _0^1 (\int _0 ^1 -\frac{\partial F_1}{\partial y}(x,y)dy)dx &= \int _0^1 [-F_1(x,y)]_{y=0}^{y=1} dx \\ &= \int _0^1 F_1(x,0) dx – \int _0^1 F_1(x,1) dx \\ &= \int _0^1 F_1 (c_1)dt -\int _0^1 F_1(c_3) dt \\ &= \int_{c_1} F + \int_{c_3} F\end{aligned} \]
が成り立ちます。同様に\(x\)に注目することで、
\[ \begin{aligned} \int _0^1 (\int _0 ^1 \frac{\partial F_2}{\partial x}(x,y)dx)dy &= \int _0^1 [F_2(x,y)]_{x=0}^{x=1} dy \\ &= \int _0^1 F_2(1,y) dy – \int _0^1 F_2(0,y) dy \\ &= \int _0^1 F_2 (c_2)dt -\int _0^1 F_2(c_4) dt \\ &= \int_{c_2} F + \int_{c_4} F\end{aligned} \]
が成り立ち、結果として
\[ \begin{aligned}\int _c F = \int _D (-\frac{\partial F_1}{\partial y}+\frac{\partial F_2}{\partial x})dxdy\end{aligned} \]
が成り立つことがわかりました。
今回は、\(D\)を正方形の領域として考えましたが、もっと一般の領域について、類似した証明を行うことができます。詳しくは杉浦「解析入門 Ⅱ」の8章を参照。
グリーンの定理の応用:回転、ポテンシャル
微積分学の基本定理\(\int _a ^b f^{\prime}(x) dx =f(b)-f(a)\)は、区間の内部\((a,b)\)における積分は、境界\(a,b\)での値に等しいという定理です。
グリーンの定理は、内部の積分が、境界における線積分の値に等しいという定理です。基本定理の結果を、2次元にもうまく拡張した、といえるでしょう。
重積分に登場する被積分関数は、\(F\)の回転(rotation, curl)と呼ばれます。
\[ \begin{aligned} \mathrm {rot}F(x,y) =-\frac{\partial F_1}{\partial y}(x,y)+\frac{\partial F_2}{\partial x}(x,y)\end{aligned} \]
上で計算したように、\(F(x,y)=(y,x)\)ならば\(\mathrm{rot} F =0\)、\(G=(y,-x)\)ならば\(\mathrm{rot} G =-2\)です。それぞれのベクトル場を図示します。
![]()
![]()
一般に、ベクトル場\(F:\mathbb{R}^N \to \mathbb{R}^N \)に対して、多変数関数\(g:\mathbb{R}^N \to \mathbb{R}\)で\(F = \nabla g\)を満たすものを、ポテンシャル関数(potential function)と呼びます。1次元ならば\(F\)のポテンシャル関数とは原始関数のことで、ポテンシャル関数は多次元への一般化と言えます。
平面・2変数においては、回転が0でなければ\(\mathrm{rot} F \neq 0\)ポテンシャル関数は存在せず、回転が0\(\mathrm{rot} F =0\)ならばポテンシャル関数が存在することが知られています。(ラング「続 解析入門 」5章を参照)
グリーンの定理\(\int _c F = \int _D \mathrm{rot} F \)によれば、\(\mathrm{rot} F =0\)ならば\(\int _c F = 0 \)です。\(D\)を広い領域として選べるならば、閉曲線\(c\)も平面内を自由に選べることになります。
物理学・力学においては、\(F\)は力を表し、その線積分を仕事\(W\)と呼びます。位置\(x(0),x(1)\)を結ぶ曲線を\(x(t)\)として、
\[ \begin{aligned}W(x(0),x(t_1)):=\int _x F\end{aligned} \]
が端点によらず一定のとき、\(F\)を保存力と呼びます。
その2点を結ぶ異なる2つの経路を考えると、必ず閉曲線\(c\)ができます。\(\mathrm{rot} F =0\)のとき、ポテンシャル関数を持つときは、\(\int _c F = 0 \)が成り立つので、経路によらず\(W(x(0),x(t_1))\)が定まります。
つまり、保存力かどうかの判定に、ポテンシャル関数を持つかどうか、回転を使った判定が有効とわかりました。
以上、グリーンの定理を例によって理解しようとし、簡単な証明を与え、応用を紹介しました。
グリーンの定理の応用としては、複素線積分の基本的な定理であるコーシーの積分定理が重要です。またラプラス方程式の解(調和関数)の平均値の性質を示すためにも使われます。
グリーンの定理は平面における定理ですが、空間における累次の定理が成り立ち、それはストークスの定理と呼ばれています。別記事で紹介予定。
ベクトル解析では、多変数や一般形の定理が登場するために直観的な理解が難しくなるかもしれませんが、今回示したような簡単な例を考えれば納得しやすいと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1981-11-15T00:00:01Z)
¥5,720
東京大学出版会 (1985-04-25T00:00:01Z)
¥3,740