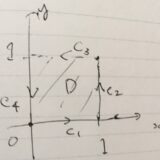どうも、木村(@kimu3_slime)です。
今回は、極座標変換による重積分の計算を、ガウス積分を例に紹介します。
ガウス積分と重積分の関係
ガウス積分とは、
\[ \begin{aligned}\int _{-\infty} ^\infty e^{-x^2} dx\end{aligned} \]
で与えられる広義積分であり、その値は\(\sqrt{\pi}\)であることが知られています。この積分は、統計学や物理学などに広く登場する重要な積分です。
この積分の値は、どうやって求めるのでしょうか。\(e^{-x^2}\)は原始関数を持たないことが知られているため、原始関数による計算はできません。
ひとつの方法が、重積分に帰着させることです。
\[ \begin{aligned}(\int _{-\infty} ^\infty e^{-x^2} dx)^2 =(\int _{-\infty} ^\infty e^{-x^2} dx)(\int _{-\infty} ^\infty e^{-y^2} dy)\\ = \int_{-\infty} ^\infty \int_{-\infty} ^\infty e^{-(x^2+y^2)}dxdy\end{aligned} \]
あえて2乗した値を考えることで、2回の逐次積分となり、(フビニの定理により)それは平面\(\mathbb{R}^2\)における重積分となります。
極座標変換による重積分の計算
問題は、重積分\(\int_{-\infty} ^\infty \int_{-\infty} ^\infty e^{-(x^2+y^2)}dxdy\)の値を求めることです。
これは直交座標\(x,y\)での計算は大変ですが、それを極座標\(r,\theta\)に変換すると楽になります。一般には、極座標への変換の結果は次の通り。
\(I=[a,b]\times[\alpha,\beta]\subset \mathbb{R}^2\)として、\(x=r\cos \theta, y=r \sin \theta\)なる変換による\(I\)の像を\(D\)とする(\(0\leq a,0\leq \alpha,\beta \leq 2\pi\))。\(D\)は扇形、または円である。\(f:D\to \mathbb{R}\)を連続関数とするとき、次の式が成り立つ。
\[ \begin{aligned}\int_D f(x,y)dxdy = \int_I f(r\cos\theta, r \sin \theta) r dr d\theta\end{aligned} \]
極座標変換した後の式に、\(r\)がかかっていることに注意しましょう。これは一般には変数変換の倍率であり、ヤコビアンと呼ばれる量です。
参考:なぜ行列式を学ぶ? 面積・体積との一致、ヤコビアンへの応用
さて、ガウス積分を求めるための極座標変換をしましょう。
\(I_R=[0,R]\times[0,2\pi]\)とすると、その極座標変換による像は円盤\(D_R = \{(x,y)\in\mathbb{R}^2 \mid x^2+y^2 \leq R^2 \}\)です。したがって、
\[ \begin{aligned} \int _{D_R} e^{-(x^2+y^2)}dxdy &= \int _{I_R} e^{-r^2 (\cos\theta) ^2 -r^2(\sin \theta)^2} r dr d\theta \\ &= \int_0 ^{2\pi } \int _0 ^R e^{-r^2} r dr d\theta \\ &= \int_0 ^{2\pi } [-\frac{1}{2}e^{-r^2}]_0 ^R d\theta \\ &= \int_0 ^{2\pi } \frac{1}{2}(1- e^{-R^2})d\theta \\ &= \pi(1- e^{-R^2}) \end{aligned} \]
となりました。ここで\(R\to \infty\)なる極限を考えると、右辺は\(\pi\)に収束し、積分領域\(D_R\)は平面\(\mathbb{R}^2 =(-\infty,\infty)\times (-\infty,\infty)\)に近づきます。
(重積分の広義積分はこれで計算できるように定義されている。詳しくは解析入門 Ⅱの7章を参照。)
よって、
\[ \begin{aligned}\int_{-\infty} ^\infty \int_{-\infty} ^\infty e^{-(x^2+y^2)}dxdy =\lim_{R\to \infty} \int _{D_R} e^{-(x^2+y^2)}dxdy =\pi\end{aligned} \]
で、ガウス積分の2乗がこの値であったことを思い出せば、
\[ \begin{aligned}\int _{-\infty} ^\infty e^{-x^2} dx = \sqrt{\pi}\end{aligned} \]
が得られました。
以上、重積分の極座標変換による計算例として、ガウス積分の値の求め方を紹介しました。
重積分の積分範囲が区間、直方体ではなく、円や扇形のときは極座標変換によって計算しやすくなります。重積分の計算が難しいときは、関数や領域に合わせて極座標変換する、という方法を思い出しましょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1981-11-15T00:00:01Z)
¥5,720
東京大学出版会 (1985-04-25T00:00:01Z)
¥3,740