どうも、木村(@kimu3_slime)です。
今回は、曲面のパラメータ表示、曲面積、球座標について紹介します。
曲面とパラメータ表示
そもそも曲面とは、空間\(\mathbb{R}^3\)の中で、2次元的に表される部分集合のことです。
例えば、2変数関数\(f:\mathbb{R}^2 \to \mathbb{R}\)のグラフ\(z=f(x,y)\)は、ひとつの曲面を表します。例えば、平面や、回転放物面、双曲放物面など。 (空間)曲線は、1変数関数\(c:[a,b]\to \mathbb{R}^3\)のグラフとして表されることを思い出しましょう。
一般に曲面は、適度になめらかな関数\(p: U \to \mathbb{R}^3\)の(像の)ことです(\(U\subset \mathbb{R}^2\))。このような曲面は2つのパラメータを使って表されるので、特にパラメータ付けられた曲面、と呼ばれます。2変数関数のグラフは、\(p(x,y)= (x,y,f(x,y))\)として理解できます。
曲面積とは
曲面\(p\)のにおける曲面積(surface area)は、次のようにして定義されます。
\[ \begin{aligned}A(p) = \int_U \|p_x \times p_y \|dxdy\end{aligned} \]
右辺の積分は重積分で、\(p_x \times p_y\)はベクトルの外積、\(\|\|\)はベクトルのノルム(大きさ)です。
一般に外積のノルムは、その2つのベクトルがなす平行四辺形の面積を表します。\(p\)がなす局所的な面積 \(\|p_x \times p_y \|\)を足し合わせたものとして、曲面積を捉えるわけです。
\(p\)が2変数関数\(f\)によって表されるもの\(p(x,y)= (x,y,f(x,y))\)である場合、\(p_x =(1,0,f_x),p_y = (0,1,f_y)\)なので、\(p_x \times p_y =(-f_x,-f_y,1)\)であり、
\[ \begin{aligned}A(p) = \int_U \sqrt{f_x ^2+f_y^2 +1}dxdy\end{aligned} \]
となります。
曲面積を計算してみましょう。
\(U=(0,1)\times(0,1)\)で、\(f(x,y)=2x-3y\)のとき、\(A = \int \int _U \sqrt{4+9+1}dxdy=\sqrt{14}\)です。この平面は、ベクトル\((1,0,2),(0,1,-3)\)によって張られる平行四辺形の面積に等しくなっています。
\(U=\{(x,y)\mid x^2+y^2 <1\}\)で、\(f(x,y)=x^2+y^2\)のとき、\(A= \int _U \sqrt{4x^2+4y^2 +1} dxdy\)です。\(x= r\cos \theta, y=r\sin \theta\)と極座標変換すると、\(U\)に対応するパラメータは\(0\leq r<1\)、\(0\leq \theta <2\pi\)です。したがって、重積分の極座標変換により、
\[ \begin{aligned} \int _U \sqrt{4x^2+4y^2 +1} dxdy &= \int_0 ^1 \int _0 ^{2\pi} \sqrt{4r^2+1} \,r d\theta dr \\ &= 2\pi [\frac{2}{3}(4r^2+1)^{\frac{3}{2}}\cdot \frac{1}{8}]_0^1 \\ &= \frac{\pi}{6} (5\sqrt{5} -1)\end{aligned} \]
と求められます。
曲面積の定義には平方根\(\sqrt{}\)を使った関数の積分が含まれ、その計算は一般には簡単ではありません。
球面極座標とは
半径\(r\)の球面\(S=\{(x,y,z)\mid x^2+y^2+z^2 =r^2 \}\)の曲面積(表面積)を求めてみましょう。
これはただひとつの\(z=f(x,y)\)のグラフとしては表せません。しかしながら、2つの変数を使って表すことはできます。
空間における直交座標の点\((x,y,z) \in \mathbb{R}^3\)を、\(x=r\sin \theta \cos\phi ,y=r \sin \theta \sin \phi,z= r \cos \theta \)と対応させるとき、\((r,\theta, \phi)\)を球座標(spherical coordinate)、3次元極座標と呼びます。ここで、\(r\geq 0\)、\(0\leq \theta \leq \pi\)、\(0\leq \phi < 2\pi\)です。
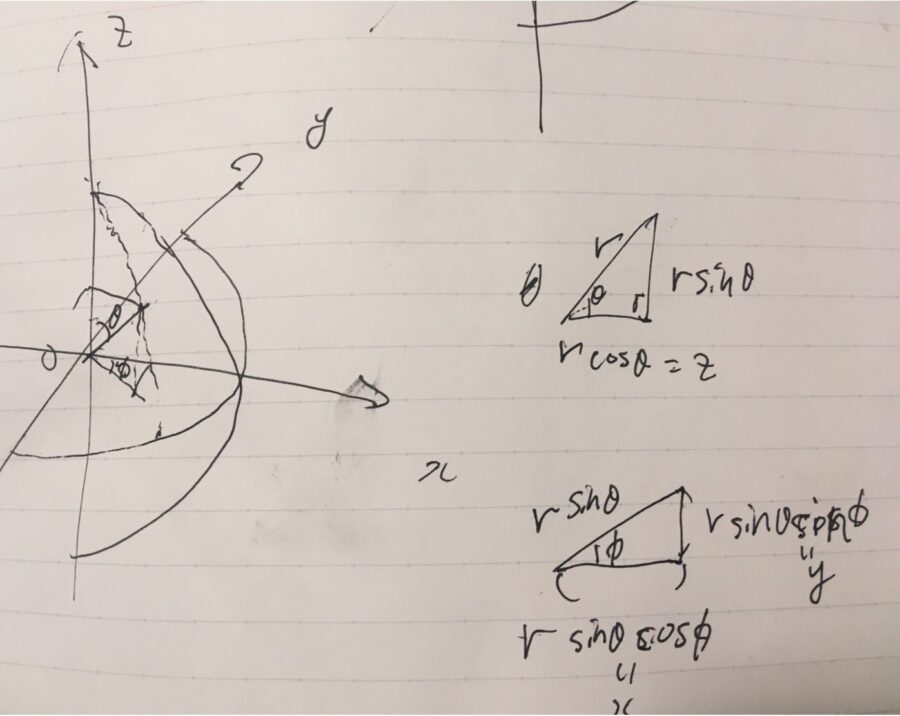
\(x^2+y^2+z^2 =r^2( (\sin \theta )^2 ((\cos \phi)^2 +(\sin \phi)^2))+(\cos \theta) ^2) =r^2\)なので、半径\(r\)の球面上の点を表します。
したがって、半径\(r\)の球面\(S\)は、\(p(\theta, \phi )=r(\sin \theta \cos \phi, \sin \theta \sin \phi, \cos \theta )\)と2変数関数によって表せます(\(r\)を固定して見ている)。地球に見立てれば、この2つの角度を表すパラメータは緯度(南北)と経度(東西)に対応するものです。
曲面積を求めてみましょう。
\(p_{\theta}=r(\cos \theta \cos \phi, \cos \theta \sin \phi, -\sin \theta )\)、\(p_{\phi}=r(-\sin \theta \sin \phi, \sin \theta \cos \phi, 0 )\)なので、\(p_{\theta} \times p_{\phi} =r^2 \sin \theta (\sin \theta \cos \phi, \sin \theta \sin \phi,\cos \theta)=r \sin \theta \,p(\theta,\phi)\)であり、\(\|p_{\theta} \times p_{\phi}\| =r ^2 \sin \theta\)となります。よって、
\[ \begin{aligned} A(p) &= \int_U \|p_{\theta} \times p_{\phi} \|d\theta d\phi \\ &=\int_0 ^{2\pi} \int_0 ^{\pi} r ^2 \sin \theta d\theta d\phi \\ &= 2\pi r^2 [-\cos \theta]_0 ^{\pi} \\ &= 4 \pi r^2\ \end{aligned} \]
となりました。ここで登場した\(\|p_{\theta} \times p_{\phi}\| =r ^2 \sin \theta\)は、空間極座標の変換倍率、ヤコビアンに等しいです。
これは球の体積\(V(r) = \frac{4}{3} \pi r^3\)を\(r\)について微分して得た表面積と一致しています。
参考:円の面積・円周、球の体積・表面積の公式の覚え方(微積分)
以上、曲面のパラメータ表示、曲面積の定義、球座標を使った球面の表面積の求め方を紹介してきました。
線積分が曲線の長さを使って定義されたように、面積分は曲面積を使って定義されます。
曲面に関する積分を考えるときは、2つのパラメータを使って表示できないか、考えてみると良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1981-11-15T00:00:01Z)
¥5,720
東京大学出版会 (1985-04-25T00:00:01Z)
¥3,740