どうも、木村(@kimu3_slime)です。
今回は、円の面積・円周、球の体積・表面積の公式の覚え方(微積分)、その導き方を紹介します。
これらを習った中学生や高校生(や大人)を読者として想定しています。微分や積分といった考え方が登場しますが、その部分は解説を加えています。詳しくわからなくても、公式の謎に迫れるのではないかと。
公式の覚え方
中学校では次のような公式を習うかと思います。
円の半径を\(r\)、同じく球の半径を\(r\)とすると、
円の面積は\(A= \pi r^2\)
円周は\(\ell = 2\pi r\)
球の体積は\(V=\frac{4}{3} \pi r^3\)
球の表面積は\(S= 4\pi r^2\)
この式を見比べていて、中学生の時の僕は何か規則性があることに気づきました。
円の面積\(A=\pi r^2\)の式において、\(r^2\)の\(2\)を前にかけて、\(r^{1}\)に置き換えた式が、\(\ell =2\pi r\)になっている。
同じようなことが球の体積でも起こっている。\(\frac{4}{3} \pi r^3\)の式で、\(r^3\)の\(3\)を前にかけて\(r^2\)に置き換えた式が、\(S= 4\pi r^2\)になっている。
つまり、片方を覚えていれば、もう一方の公式に自身がなくても、検算のようなことができるのではないか。少し法則性が見えて、覚えやすいじゃないか。そう思っていました。
微分の規則性
これは高校数学で学ぶ微積分の立場から説明されます。とりあえず事実を紹介しましょう。
\(f(x)=x^2\)のような関数は、「微分」という操作が行えます。\(x^2\)の微分は\(f^{\prime}(x)=2x\)です。\(f(x)=x^3\)の微分は、\(f^{\prime}(x)=3x^2\)です。\(x\)のべき乗の次数を掛け算にして、次数を一個下げる操作となります。
(一般には、\(n\)を1以上の自然数とするとき、\(f(x)= x^{n}\)の微分は\(f^{\prime}(x) =n x^{n-1}\)となります。)
円の面積を半径\(r\)の関数として\(A(r)= \pi r^2\)みましょう。すると、その微分が\(A^{\prime} (r)= \pi 2 r^{2-1} = 2\pi r=\ell(r)\)です。
球の体積も半径\(r\)の関数として\(V(r)= \frac{4}{3} \pi r^3\)見ます。その微分を計算すれば、\(V^{\prime}(r) = \pi 4 r^{3-2} =4\pi r^2= S(r)\)です。
積分の規則性
微分という操作の逆を辿ることもできます。微分して\(x\)になる関数は、\(\frac{1}{2} x^2\)です(確かめてみてください)。微分して\(x^2\)になる関数は\(\frac{1}{3}x^3\)です。
この微分という操作の逆は、積分と呼ばれ、次のように表されます。
\[ \begin{aligned}\int x dx =\frac{1}{2} x^2\end{aligned} \]
\[ \begin{aligned}\int x^2 dx =\frac{1}{3}x^3\end{aligned} \]
この記号を使えば、今までの公式を逆に見ることもできます。
円周の公式を覚えているけど、円の面積を忘れてしまった。そんなときは円周を積分すれば良いです。\(\int \ell (r) dr= 2\pi \frac{1}{2} r^2 = \pi r^2 =A(r) \)
球の表面積\(S(r)= 4\pi r^2\)から出発すれば、\(\int S(r)dr =4\pi \frac{1}{3} r^3 =\frac{4}{3}\pi r^3 =V(r)\)と球の体積が求められました。
以上が、円や球の公式の統一的な覚え方です。
どうして公式は成り立つのか
では、どうして中学で学ぶような円や球の公式が成りたつのでしょうか。
そもそも、面積や体積とは何なのか。それは厳密には、高校における「積分」によって定義される量です。
ここでは簡単にそのアイデアを紹介します。
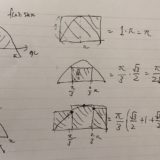
次の図のように、面積は細かい線の長さを足し合わせたものとして計算されます。
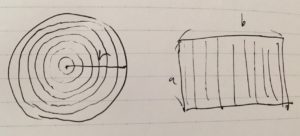
例えば長方形の面積は、2つの辺の長さを\(a,b\)として、\(A=ab\)と約束されます。これは面積の基本的な定義です。この式は、\(a\)の長さの直線を幅\(b\)まで足し合わせたもの……と見ることができます。
\[ \begin{aligned}A= \int _0 ^b a dx = a \cdot(b-0)=ab\end{aligned} \]
同じ発想で、円の面積について考えてみましょう。円を円周を足し合わせたものとして見るわけです。
半径\(r\)の円の円周は、\(\ell(r) =2r \cdot \pi\)となります。そもそも円周率\(\pi\)は、円周\(\ell(r)\)と直径\(2r\)との長さの比\[ \begin{aligned}\pi :=\frac{\ell(r)}{2r}\end{aligned} \]と定義されるのでした。
そして円の面積は、\(\ell (r)=2\pi r\)を足し合わせたもの(積分)として定義されます。
\[ \begin{aligned}A:= \int _0 ^r \ell(s) ds =[\pi s^2]_0 ^{r}= \pi r^2\end{aligned} \]
と円の面積が求まりました。
面積は積分によって定義されますが、積分の計算は「微分の逆」として行えます。微積分学の基本定理として知られる素晴らしい発見で、面積の話とセットで微分が登場するのはそういう事情があるわけです。
次いで球の体積を求めてみます。
キャベツを輪切りにするようにして、できた輪の面積を足し合わせたものが球の体積です。
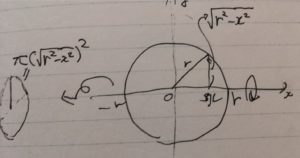
図のように置きます。直角三角形の斜辺が\(r\)、底辺が\(x\)のとき、高さはピタゴラスの定理より\(\sqrt{r^2-x^2}\)となります。この高さの線分を\(x\)軸の周りに回転させると円ができますが、その面積はさきほどの計算より、\(\pi (\sqrt{r^2-x^2})^2 =\pi (r^2-x^2)\)です。
この球の断面積\(\pi (r^2-x^2)\)を、\(-r \leq x\leq r\)まで足し合わせたもの・積分が、球の体積\(V(r)\)となります。
\[ \begin{aligned} V(r) &=\int _{-r} ^r \pi (r^2-x^2)dx \\ &=\pi [r^2 x -\frac{1}{3} x^3]_{-r}^r \\ &=\pi (2r^3-\frac{2}{3} r^3 )\\ &=\frac{4}{3} \pi r^3\end{aligned} \]
と求められました。
この体積\(V(r)\)は、半径\(r\)の球の表面積を足し合わせたものとして見ることができます。つまり、\(V(r)\)を\(r\)について微分したものが表面積\(S(r)\)となります。
\[ \begin{aligned}V^{\prime} (r) = 3\cdot \frac{4}{3} \pi r^{3-2} = 4\pi r^2 \end{aligned} \]
細かくは説明しませんが、扇形の面積と弧の長さも同じ関係にあります。
半径を\(r\)、中心角を\(\theta\)とすると、
\[ \begin{aligned}A(r) = \frac{1}{2}r^2 \theta\end{aligned} \]
\[ \begin{aligned}\ell(r) =r \theta\end{aligned} \]
です。円弧の長さがこのように表されるのは、角度(ラジアン)の定義によります。円弧の積み重ね・積分が扇形の図形の面積です。
参考:ラジアン(弧度法)を学ぶのはなぜ? 三角関数の微分を単純化
単純に、円の面積を中心角\(2\pi\)(\(360^{\circ}\))の扇形と見て、面積は中心角の大きさに比例するので、扇形は円の面積の\(\frac{\theta}{2\pi }\)倍である。よって、扇形の面積を\(A(r) = \frac{1}{2}r^2 \theta\)と求めても良いでしょう。弧の長さはその微分として得られます。
角錐や円錐の体積や表面積は、円の面積や扇形の面積から導けます。
今回は、円や球の面積・体積、円周・表面積の公式の相互関係を、微分と積分の概念を交えて紹介しました。
これらの式が似ているのは偶然ではなく、その背後に面積の定義式=積分、その変化率=断片長や断面積を表す微分が登場しているのです。
面積や体積の式は、小学校や中学校で覚えなさいと言われますが、それは高校の微積分を学べば解決します。面積や体積計算の先には、こんな数学があることを知ってもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。