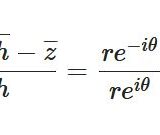複素関数の線積分とは：具体例をもとに

どうも、木村（@kimu3_slime）です。

複素解析における重要な結果として、コーシーの積分定理や留数定理がありますが、その理解にあたってはまず複素関数の積分を知る必要があるでしょう。

今回は、複素関数の線積分とは何か、具体例をもとに紹介します。

複素関数の線積分とその性質
複素積分の具体例
こちらもおすすめ

複素関数の線積分とその性質

なぜ、複素関数の積分を考えるのでしょうか。

数学者のコーシーは、実積分や虚数について調べるうちに、複素積分の理論にたどり着きました。そこで得られたのが、コーシーの積分定理や留数定理と呼ばれる結果です。複素積分という広い立場から見ることで、指数積分や三角積分、フレネル積分など、計算しにくい多くの実積分・広義積分が計算できるようになる、というメリットがあります。

では、複素関数\(f(z)\)の積分を考えてみましょう。

高校で考えたような積分、実数変数で1変数の積分なら、実数直線上の区間\([a,b]\)で、\(\int _a ^b f(x)dx\)というものを考えることができました。

複素関数を考えると、積分する経路は、実数直線上だけでなく複素平面に広がっています。そこで多変数の実数値関数と同様に、線積分を考えることができます。

\(f\)を連続な複素関数、\(c: [a,b] \to \mathbb{C}\)を単純な（＝自己交差のない）曲線として、

\[ \begin{aligned}\int _c f(z) dz := \int_a ^b f(c(t)) c^{\prime}(t) dt\end{aligned} \]

と複素線積分（complex integration）を定めます。

（厳密に言うと、同一の曲線でも異なるパラメータ付けの仕方があって、それによって右辺の積分値は変わりうるように見えます。が、異なるパラメータ付けであっても同じ値になり、問題なく複素積分は定義されることが一般に知られています。）

\(c\)が長方形のように、有限個の折れ曲がった部分を持つ曲線（＝区分的になめらかな曲線）ならば、積分はなめらかな部分に切り分けて足し合わせたものとして定義されます。

線積分の定義の右辺は、実変数で複素数値の関数の積分です。\(f(t)=u(t) +iv(t)\)と実部虚部に分けて表されるとき、

\[ \begin{aligned}\int_a ^b f(t) dt := \int_a ^b u(t) +i \int_a ^b v(t)\end{aligned} \]

と素直に定義します。つまり、複素線積分の値は一般に複素数です。

単純な曲線\(c\)の具体例を考えましょう。

例えば、\(c(t) =t+it, 0\leq t \leq 1 \)という実変数で複素数値の関数\(c:[0,1]\to \mathbb{C}\)は、\(z=0\)から\(z=1+i\)をつなぐ直線を表しています。

\(c(t)= e^{it}, 0 \leq t \leq 2\pi\)という曲線は、オイラーの公式\(e^{it} = \cos t + i \sin t\)より、\(z=1\)から出発して反時計回りに一周して\(z=1\)に戻ってくる、原点を中心とした円を描く曲線です。

特に、始点と終点が一致する\(c(a)=c(b)\)曲線は、閉曲線（closed curve）と呼ばれます。複素積分の理論では、特に閉曲線上の積分が重要であることが、後に明らかになるでしょう。

複素積分の具体例

では、複素積分を簡単なケースで計算してみましょう。

複素積分は、関数の変数\(z\)を曲線上の点\(c(t)\)に置き換え、\(c^{\prime}(t)\)をかけて\(t\)について積分したものです。

\(c(t) = t+it , 0 \leq t \leq 1\)において、\(f(z)=z\)を積分してみましょう。\(c^{\prime}(t) =1+i\)となるので、

\[ \begin{aligned} \int _c z dz &= \int_0 ^1 (t+it)(1+i) dt \\&= \int _0 ^1 2ti dt \\ &= i [t^2]_0 ^1 \\ &= i\end{aligned} \]

となります。積分の結果として複素数が登場していますね。

後に得られる結果を見据えると、\(c(t)= e^{it}, 0 \leq t \leq 2\pi\)という反時計回りの経路での積分が特に大事です。以降、ずっとこの曲線上の積分を考えます。ここでは\(c^{\prime }(t) = i e^{it}\)となりますね。

\[ \begin{aligned} \int_c z dz &= \int _0 ^{2\pi} e^{it} i e^{it}dt \\&= [\frac{i}{2i}e^{2it}]_0 ^{2\pi} \\&= 0 \end{aligned} \]

\[ \begin{aligned} \int_c z^2 dz &= \int _0 ^{2\pi} e^{2it} i e^{it}dt \\&= [\frac{i}{2i}e^{3it}]_0 ^{2\pi} \\&= 0 \end{aligned} \]

同様にすれば、正のべき乗については、\(\int_c z^n dz=0\)となりますね。

さらに、指数関数や三角関数についても、微積分学の基本定理を使うことで、

\[ \begin{aligned} \int_c e^z dz &= \int _0 ^{2\pi} e^{c(t)} c^{\prime }(t)dt \\ &= \int _0 ^{2\pi} \frac{d}{dt}(e^{c(t)} )dt\\&= [e^{c(t)}]_0 ^{2\pi} \\&= 0 \end{aligned} \]

\[ \begin{aligned} \int_c \sin z dz &= \int _0 ^{2\pi} \sin (c(t)) c^{\prime }(t)dt \\ &= \int _0 ^{2\pi} \frac{d}{dt}(- \cos (c(t)) )dt\\&= [-\cos (c(t))]_0 ^{2\pi} \\&= 0 \end{aligned} \]

となります（\(\cos\)も同様）。

一般には、\(f\)が開集合\(D \subset \mathbb{C}\)において連続で、曲線\(c: [a,b]\to \mathbb{C}\)が\(D\)に含まれていて、\(F^{\prime} =f\)となるような正則関数（つまり、原始関数）が存在するとき、

\[ \begin{aligned}\int _c f(z)dz = F(c(b))- F(c(a))\end{aligned} \]

が成り立ちます。閉曲線ならばその値は\(0\)です。

これらの結果は、「閉曲線が囲む領域において正則な関数の、その閉曲線における積分は0になる」というコーシーの積分定理に一般化されます。

これは実変数の積分と似た結果に見えるかもしれませんが、そう捉えないように注意しましょう。実微分可能性と、複素微分可能性（正則関数）は別物です。複素の意味での「原始関数」は、強い条件を要求しています。

例えば、\(f(z) =\frac{1}{z}\)は原始関数を持ちません。

「\((\log z) ^{\prime} = \frac{1}{z}\)だから（\(|z-1|<1\)という収束半径内でなければ誤り）、\(\int_c \frac{1}{z} dz =0\)」と考えないように注意しましょう。実際は、

\[ \begin{aligned} \int_c \frac{1}{z} dz &= \int _0 ^{2\pi} \frac{1}{e^{it}} i e^{it}dt \\&= 2 \pi i \end{aligned} \]

となります。うまいこと\(e^{\pi i}\)がキャンセルしたので、積分の値が\(0\)でなく\(2 \pi i \)と残っています。

さらに負のべきを考えると、

\[ \begin{aligned} \int_c \frac{1}{z^2} dz &= \int _0 ^{2\pi} \frac{1}{e^{2it}} i e^{it}dt \\&= [\frac{i}{-i}e^{-it}]_0 ^{2\pi} \\&= 0 \end{aligned} \]

です。一般に、整数べきの関数の積分は\(\int _c z^k dz\)については、\(k \neq -1\)ならば\(0\)、\(k=-1\)のときのみ\(2\pi i \)となります。ちょっと不思議な感じがしますね。

これはコーシーの積分公式、留数定理と呼ばれる結果につながっています。

以上、複素関数の線積分とその性質を、具体例をもとに紹介してきました。

コーシーの積分公式や留数定理は便利な結果ですが、そもそも複素積分が何を意味しているのか、今回のような単純なケースで知っておくのは大事だと思います。

木村すらいむ（@kimu3_slime）でした。ではでは。