三角関数の直交性とは：フーリエ級数展開と関数空間の内積

どうも、木村（@kimu3_slime）です。

今回は、三角関数の直交性とは何か、フーリエ級数展開と関数空間の内積について紹介します。

フーリエ級数展開と関数空間の内積
三角関数の直交性
こちらもおすすめ

フーリエ級数展開と関数空間の内積

18世紀の数学者・物理学者のジョゼフ・フーリエ（Fourier）は、固体の内部における熱伝導の時間発展について、すなわち熱伝導方程式を研究し、次のようなアイデアにたどり着きました。

任意の関数は、三角関数の無限和（フーリエ級数）として展開できる。

\[\begin{aligned} f(x)&=a_0 + a_1 \cos x + b_1 \sin x \\&+a_2 \cos 2x+ b_2 \sin 2x +\cdots \end{aligned} \]

「任意の関数」の意味合いは後に厳密化されていましたが、「三角関数に分解できる」というアイデアは正しく有効なものです。

試しに、次の角張った関数（矩形波）をフーリエ級数展開し、グラフで表してみましょう。

\[ \begin{aligned}f(x)= \begin{cases}0 & (-\pi <x <0 )\\1 & (0<x <\pi)\end{cases}\end{aligned} \]

計算は省略しますが、\(\cos \)の成分はすべて消え、\(\sin\)は\(k\)が奇数のもののみ残ります。

\[ \begin{aligned}f(x)= \frac{1}{2} + \frac{2}{\pi} \sin x + \frac{2}{3\pi} \sin 3x + \frac{2}{5\pi} \sin 5x+ \cdots\end{aligned} \]

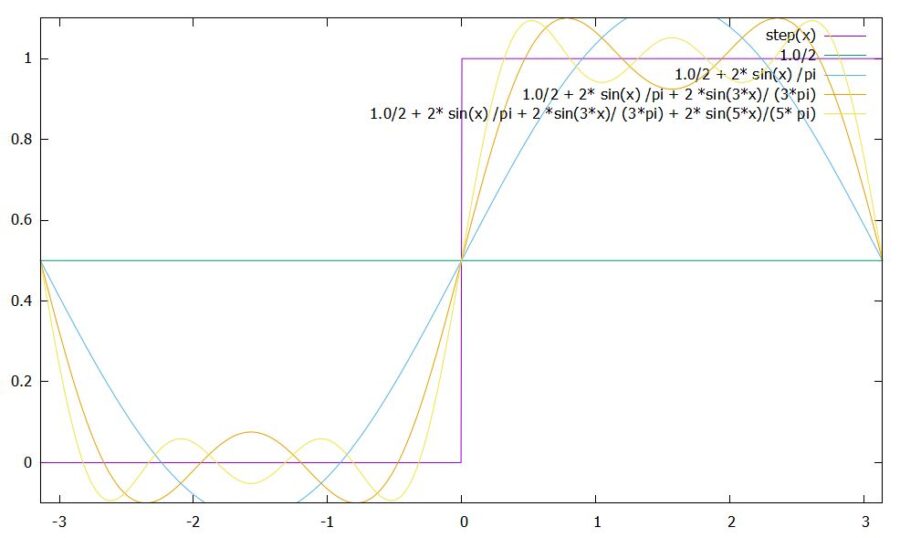
最初は\(\frac{1}{2}\)という定数関数で近似する。続いて、そこに\(\sin x\)の成分を加える。さらに、より起伏の数が多い\(\sin 3x\)の成分を加えることで、\(\sin x\)の山が平らになるようにしていく。……この繰り返しにより、グラフは限りなくもとの角張った関数に近づいていきます。

もとの関数\(f\)と三角関数の内積（これはフーリエ係数と呼ばれる）

\[ \begin{aligned}a_0= \frac{1}{2\pi } \langle f, 1\rangle ,\quad a_k =\frac{1}{\pi } \langle f, \cos kx\rangle,\quad b_k =\frac{1}{\pi } \langle f, \sin kx \rangle\end{aligned} \]

は、もとの関数のうち、どれだけの強さ（振幅）でその三角関数の成分が含まれているかを示すものです。今回の例ならば、\(\cos \)成分はすべて\(0\)で、\(\sin x\)成分は\( \frac{2}{\pi}\)、\(\sin 2x\)成分は\(0\)、\(\sin 3x\)成分は\( \frac{2}{3\pi} \)となっています。

関数がこのように三角関数の和として展開できるのは、三角関数の集まり\(\{\cos 0x, \cos kx, \sin kx\}_{k=1}^{\infty}\)がある意味で直交しているからです。

関数の直交を考えるには、関数のなす線形空間（関数空間）を考え、そこに内積を定める必要があります。

\(n\)を自然数、\(L>0\)、\(I =[-\pi,\pi]\)として、

\[ \begin{aligned}V_n:= \{f:I \to \mathbb{R} \mid f(x)=a_0+\\ \sum_{k=1} ^n (a_k \cos kx +b_k \sin kx) ,\quad a_k,b_k \in \mathbb{R}\}\end{aligned} \]

という三角関数の和で表される関数の集合\(V_n\)を考えましょう。これは

\[ \begin{aligned}(f+g )(x) =f(x)+g(x)\end{aligned} \]

\[ \begin{aligned}(\lambda f) (x) = \lambda f(x)\end{aligned} \]

により関数の和、スカラー倍を定めることにより、線形空間となります。例えば、\(f(x)=a_0+ \sum_{k=1} ^n (a_k \cos kx +b_k \sin kx)\),\(g(x)=c_0+ \sum_{k=1} ^n (c_k \cos kx +d_k \sin kx)\)と表すと、その和は

\[ \begin{aligned}f+g(x)=(a_0+c_0)\\+ \sum_{k=1} ^n ((a_k+c_k) \cos kx +(b_k+d_k) \sin kx)\end{aligned} \]

となるので、\(f+g \in V_n\)です。スカラー倍も同様で、他の性質は関数空間の一般的な証明と同様です。

一般にフーリエ級数と呼ぶときは無限和を考えますが、今回は\(n\)個までの和、有限フーリエ級数を考えています。直交性の議論は\(n\)が何であっても通用するものです。

さて、線形空間\(V_n\)に積分によって内積を定めたいです。

\[ \begin{aligned}\langle f,g \rangle:= \int _{-\pi} ^\pi f(x)g(x) dx\end{aligned} \]

と定義します。

\(f,g \in V_n\)とすると、\(f,g\)は連続関数の和なので連続関数であり、その積\(fg\)も連続です。したがって、考えている区間\(I=[-\pi,\pi]\)は有界なので、関数は最大値・最小値を持ち、積分\(\langle f,g \rangle\)は有限の値を持つことが保証されています。

\(\langle \cdot, \cdot \rangle\)が内積の定義を満たすことを確認しましょう。積分の線形性を使っています。

\[ \begin{aligned} \langle f,g \rangle &= \int _{-\pi} ^\pi f(x)g(x) dx \\ &= \int _{-\pi} ^\pi g(x)f(x) dx \\ &= \langle g,f \rangle\ \end{aligned} \]

\[ \begin{aligned} \langle \lambda f+h,g \rangle &= \int _{-\pi} ^\pi (\lambda f(x)+h(x))g(x) dx \\ &= \lambda \int _{-\pi} ^\pi f(x)g(x) dx + \int _{-\pi} ^\pi h(x)g(x) dx \\ &= \lambda \langle f,g \rangle +\langle h,g \rangle\ \end{aligned} \]

\[ \begin{aligned} \langle f,f \rangle &= \int _{-\pi} ^\pi (f(x))^2 dx \\ & \geq 0 \ \end{aligned} \]

で、\(f(x)=0\)のときは\(\langle f,f\rangle=0\)です。

以上により、\(\langle \cdot, \cdot \rangle\)が\(V_n\)の内積であることが示せました。

内積があると、関数\(f,g\)が直交している（orthogonal）とは、\(\langle f,g \rangle= 0\)であると定義できます。

三角関数の直交性

では、サイン・コサインといった三角関数\(\{\cos 0x, \cos kx, \sin kx\}_{k=1}^{n}\)が\(V_n\)において直交していることを示しましょう。

\(\cos 0x =1\)という定数関数は例外的です。これと\(\cos kx , \sin kx\)の直交性を調べてみましょう。それらの内積は、単に三角関数の積分となります。

サインの\(I=[-\pi, \pi]\)における積分は0になります。一般に、\(f\)を奇関数（\(f(x)=-f(x)\)）を満たす関数とすると、原点について対称な区間\(I\)における積分は\(\int f(x)dx =0\)です。サイン\(\sin kx\)は奇関数なので、\(\langle \cos 0x , \sin kx \rangle=0\)です。

一方、コサイン\(\cos kx\)との積分は

\[ \begin{aligned} \langle \cos 0x , \cos kx\rangle&= \int _{-\pi}^{\pi} \cos kx dx\\ &= [ \frac{1}{k}\sin kx]_{-\pi} ^\pi \\ &= 0 \end{aligned} \]

です。ここでサインが\(\pi\)を周期とする関数で、\(\sin k\pi =0\)を使っています。これが使えるように区間を\(I=[-\pi,\pi]\)としました。

続いて、コサイン同士、サイン同士、サインコサインの直交性を調べましょう。\(k \neq \ell\)とします。

三角関数の積の積分計算には、三角関数の加法定理から導かれる積和の公式が有効です。

\[ \begin{aligned}\cos \alpha \cos \beta =\frac{1}{2}(\cos (\alpha +\beta) +\cos (\alpha -\beta))\end{aligned} \]

\[ \begin{aligned}\sin \alpha \sin \beta =\frac{1}{2}(-\cos (\alpha +\beta) +\cos (\alpha -\beta))\end{aligned} \]

\[ \begin{aligned}\cos \alpha \sin \beta = \frac{1}{2}(\sin (\alpha +\beta)-\sin (\alpha -\beta))\end{aligned} \]

\[ \begin{aligned} \langle \cos kx , \cos \ell x\rangle&= \int _{-\pi}^{\pi} \cos kx \cos \ell x dx\\ &= \frac{1}{2} \int _{-\pi}^{\pi} (\cos (k+\ell)x +\cos (k-\ell)) x dx \\&= \frac{1}{2} [ \frac{1}{k+\ell}\sin (k+\ell)x +\frac{1}{k-\ell}\sin (k-\ell)x]_{-\pi} ^\pi \\ &= 0 \end{aligned} \]

\[ \begin{aligned} \langle \sin kx , \sin \ell x\rangle&= \int _{-\pi}^{\pi} \sin kx \sin \ell x dx\\ &= \frac{1}{2} \int _{-\pi}^{\pi} (-\cos (k+\ell)x +\cos (k-\ell)) x dx \\&= \frac{1}{2} [ -\frac{1}{k+\ell}\sin (k+\ell)x +\frac{1}{k-\ell}\sin (k-\ell)x]_{-\pi} ^\pi \\ &= 0 \end{aligned} \]

\[ \begin{aligned} \langle \cos kx , \sin \ell x\rangle&= \int _{-\pi}^{\pi} \cos kx \sin \ell x dx\\ &= \frac{1}{2} \int _{-\pi}^{\pi} (\sin (k+\ell)x -\sin (k-\ell)x) dx \\&= 0 \end{aligned} \]

最後は奇関数の積分が0ということです。

以上により、三角関数\(\{\cos 0x, \cos kx, \sin kx\}_{k=1}^{n}\)が直交していることがわかりました。線形空間において直交しているベクトルは線形独立なので、

さらに、それぞれの関数のノルムを1にして、正規直交基底を得ておくと、関数を展開するときに便利です。

関数のノルムは、内積により\(\|f\| := \sqrt{\langle f, f \rangle}\)と定義できます。定数関数、コサイン、サインのノルムを計算してみましょう。

\[ \begin{aligned} \|\cos 0x \| &= \sqrt{ \int _{-\pi}^{\pi} 1 dx }\\ &= \sqrt{2\pi} \end{aligned} \]

\[ \begin{aligned} \|\cos kx \| &= \sqrt{ \int _{-\pi}^{\pi}( \cos kx)^2 dx }\\&= \sqrt{\frac{1}{2} \int _{-\pi}^{\pi} (\cos 2k x +1) dx }\\ &= \sqrt{\frac{1}{2}[\frac{1}{2k}\sin 2kx +x]_{-\pi} ^\pi }\\ &= \sqrt{\pi} \end{aligned} \]

\[ \begin{aligned} \|\sin kx \| &= \sqrt{ \int _{-\pi}^{\pi}( \sin kx)^2 dx }\\&= \sqrt{\frac{1}{2} \int _{-\pi}^{\pi} (-\cos 2k x +1) dx }\\ &= \sqrt{\frac{1}{2}[-\frac{1}{2k}\sin 2kx +x]_{-\pi} ^\pi }\\ &= \sqrt{\pi} \end{aligned} \]

と求められました。

よって、\(\{ \frac{1}{\sqrt{2\pi}}\cos 0x, \frac{1}{\sqrt{\pi}}\cos kx, \frac{1}{\sqrt{\pi}}\sin kx\}_{k=1}^{n}\)は\(V_n\)の正規直交なベクトルです。

\(V_n\)の関数はすべてこれらの和で表せるので、これらは正規直交基底と言えます。\(V_n\)の次元は、\(2n +1\)ですね。

今回は区間を\((-\pi,\pi)\)で考えましたが、\(L>0\)として\((-L,L)\)で同様の議論ができます。そのときは\(y= \frac{L}{\pi}x\)と変数変換すれば良く、\(\cos \frac{\pi}{L}kx ,\sin \frac{\pi}{L}kx\)が直交系となります。

また、今回は限定的な関数空間\(V_n\)を考えましたが、（ルベーグの意味で）2乗可積分のなす空間\(L^2\)において、三角関数系が完全正規直交基底となることが示せます。今回は、その議論の基礎となるケース、どんな有限個を考えても正規直交基底が得られることを扱いました。

参考：線形代数の応用：関数の「空間・基底・内積」を使ったフーリエ級数展開

以上、三角関数が直交することについて、フーリエ級数展開と関数空間の内積から話を始めて紹介してきました。

関数が「直交する」ということのイメージは最初のうちは湧きにくいかもしれませんが、その議論を支えているのは、まず関数のなす線形空間があること、そこに積分により定まる内積があることです。

フーリエ級数展開においてフーリエ係数とは、展開したい関数と三角関数の内積として現れます。ぜひ、関数の内積、特に三角関数との内積の扱いに慣れてみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。