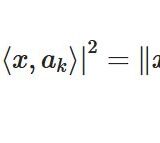どうも、木村(@kimu3_slime)です。
線形代数学では、正規直交基底というものをよく考えます。
今回は、多項式のなす空間における直交系、直交多項式について、ルジャンドル多項式を例に紹介します。
直交多項式とは
直交多項式(orthogonal polynomial)とは、関数の内積について直交した多項式たちのことです。いくつか有名な直交多項式が知られていますが、今回はルジャンドル多項式と呼ばれるものを考えてみましょう。
関数の直交性を考えるためには、内積が必要です。今回は、区間\([-1,1]\)において2乗可積分関数のなす関数空間\(L^2\)において、
\[ \begin{aligned}\langle f,g\rangle := \int_{-1}^1 f(x)g(x) dx\end{aligned} \]
という積分により定義された内積を考えましょう。多項式関数は連続であり、有界な閉区間\([-1,1]\)上で最大値と最小値を持つため、\(L^2\)に属しています。
\(n\)次のルジャンドル多項式(Legendre polynomial)\(P_n(x)\)とは、\(n\)次の多項式であり、\(n-1\)次のルジャンドル多項式すべてと直交し、\(P_n(1)=1\)を満たすような多項式と定義します。
\((1,x,x^2,x^3,\dots)\)といった多項式関数を、上で定めた内積を使って直交化することによって、低次のルジャンドル多項式を具体的に求めてみましょう。
(\((1,x,x^2,x^3,\dots)\)といった多項式関数は、線形独立であることが知られています。つまり、この関数空間は無限次元です。)
\(P_0 (x)=k_0\)と文字で置きます。\(P_0(1)=1\)より、\(P_0 (x)=1\)とすれば良いわけです。
\(P_1 (x) = k_1x+k_0\)と置きましょう。\(P_0\)と直交していることから、
\[ \begin{aligned} \langle P_0,P_1\rangle&=\int_{-1}^1 1(k_1 x+k_0) dx\\&=\int_{-1}^1 k_0 dx \\&= 2k_0 \\&=0 \end{aligned} \]
です。一般に、原点について対称な区間における奇関数の積分は0であり、奇数次の項は奇関数なので、それらの積分は0になります。偶数次のみ計算すれば良いことに注意しましょう。
すなわち、\(k_0=0\)。\(P_1(1)=1\)より、\(k_1=1\)。\(P_1(x)=x\)となりました。
どんどん直交化して、\(P_2,P_3\)まで求めてみましょう。
\(P_2(x) =k_2x^2+k_1x+k_0\)とします。\(P_0,P_1\)との直交性から、
\[ \begin{aligned} \langle P_0,P_2\rangle&=\int_{-1}^1 1(k_2x^2+k_1x+k_0) dx\\&=\int_{-1}^1 k_2x^2+k_0dx \\&= \frac{2}{3}k_2+2k_0 \\&=0 \end{aligned} \]
\[ \begin{aligned} \langle P_1,P_2\rangle&=\int_{-1}^1 x(k_2x^2+k_1x+k_0) dx\\&=\int_{-1}^1 k_1x^2dx \\&= \frac{2}{3} k_1 \\&=0 \end{aligned} \]
で、\(P_2(1)= 1\)より\(k_2+k_0=1\)。これらを解けば、\(k_0 =-\frac{1}{2}\)、\(k_2 =\frac{3}{2}\)で、\(P_2(x) = \frac{1}{2}(3x^2 -1)\)となりました。
\(P_3 (x)=k_3 x^3 +k_2 x^2 +k_1x +k_0\)とします。\(P_0,P_1,P_2\)との直交性から、
\[ \begin{aligned} \langle P_0,P_3\rangle&=\int_{-1}^1 1(k_3 x^3 +k_2 x^2 +k_1x +k_0) dx\\&=\int_{-1}^1 k_2 x^2 +k_0dx \\&= \frac{2}{3}k_2+2k_0 \\&=0 \end{aligned} \]
\[ \begin{aligned} \langle P_1,P_3\rangle&=\int_{-1}^1 x(k_3 x^3 +k_2 x^2 +k_1x +k_0) dx\\&=\int_{-1}^1 k_3x^4+k_1 x^2 dx \\&= \frac{2}{5}k_3+\frac{2}{3}k_1 \\&=0 \end{aligned} \]
\[ \begin{aligned} \langle P_2,P_3\rangle&=\frac{1}{2}\int_{-1}^1 (3x^2-1)(k_3 x^3 +k_2 x^2 +k_1x +k_0) dx\\&=\frac{1}{2}\int_{-1}^1 3x^4 k_2+3x^2 k_0-k_2x^2 -k_0 dx \\&= \frac{3}{5}k_2+k_0-\frac{1}{3}k_2-k_0 \\&=0 \end{aligned} \]
となり、\(k_2=k_0=0\)がわかります。\(P_3(1)=k_3+k_1=1\)と合わせると、\(k_3=\frac{5}{2},k_1=-\frac{3}{2}\)です。よって、\(P_3 (x) =\frac{1}{2}(5x^3-3x)\)となりました。
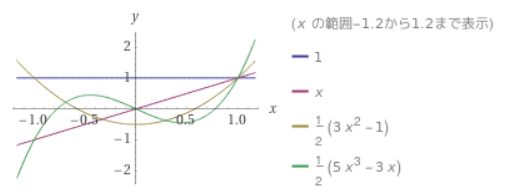
画像引用:WolframAlpha
ルジャンドル多項式とは
以上のような手順で、直交する多項式\(P_n\)を帰納的に求めることができます。ルジャンドル多項式にはいくつかの定義・表示式が知られていて、
\[ \begin{aligned}P_n(x) =\frac{1}{2^n n!} \frac{d^n}{dx^n}( (x^2-1)^n)\end{aligned} \]
\[ \begin{aligned}\frac{1}{\sqrt{1-2xt+t^2}} = \sum^\infty _{n=0} P_n(x) t^n\end{aligned} \]
を満たします。
前者はロドリゲスの公式(Rodrigues’ formula)と呼ばれるものです。
後者は左辺のテイラー展開の係数として表れる多項式がルジャンドル多項式という主張ですが、これはニュートンポテンシャルの極座標表示を近似計算するときなどに現れ、物理に応用されています。
ルジャンドル多項式の特に重要な性質として、\(P_n\)は
\[ \begin{aligned}(1-x^2)y^{\prime \prime}(x) -2xy^{\prime}(x) +n(n+1)y(x) =0\end{aligned} \]
という微分方程式を満たします。これはルジャンドルの微分方程式(Legendre differential equation)と呼ばれるものです。
\(P_0(x)=1,P_1(x)=x\)、\(P_2(x) = \frac{1}{2}(3x^2 -1)\)、\(P_3 (x) =\frac{1}{2}(5x^3-3x)\)が微分方程式を満たすことを確かめてみましょう。
\(P_0\)については、微分の項は消え、\(n=0\)なので左辺は\(0\)なので、自明な意味で等式が成り立っています。
\(P_1\)について。2回微分の項はありません。\(-2xP_1^{\prime}=-2x \)で、\(1\cdot2 P_1 =2x\)なので、等式を満たします。
\(P_2\)について。\((1-x^2)P_2^{\prime \prime }=3(1-x^2)\)、\(-2xP_2^{\prime}(x)=-6x^2\)、\(2\cdot 3 P_2 (x)=3(3x^2-1)\)で、足し合わせれば0です。
\(P_3\)について。\((1-x^2)P_3^{\prime \prime }=15x(1-x^2)\)、\(-2xP_3^{\prime}(x)=-x(15x^2-3)\)、\(3\cdot 4P_3(x)=6(5x^3-3x)\)で、足し合わせると0ですね。
直交多項式がある種の微分方程式を満たしている、というのは不思議に思えるかも知れません。一般に、
\[ \begin{aligned}\frac{d}{dx}(p(x) \frac{dw}{dx}(x)) + \{q(x)+ \lambda r(x)\}w(x) =0\end{aligned} \]
といった形の微分方程式は、ストゥルム・リウビル型微分方程式と呼ばれます。
\(p(x)=1-x^2\)、\(q(x)=0\)、\(\lambda = n(n+1)\)、\(r(x)=1\)として、ルジャンドルの微分方程式を含んでいますね。ルジャンドル多項式とは、微分方程式の左側を微分作用素としてまとめたときの、\(n(n+1)\)を固有値とする固有関数というわけです。
ストゥルム・リウビル型の微分方程式は、ある種の固有値問題であり、その解(固有関数)は互いに直交していることが知られています。ルジャンドル多項式のような直交多項式の背景には、こうした理論(ストゥルム・リウビル理論)があった、と言えるでしょう。
ルジャンドル多項式の他にも、エルミート多項式、ラゲールの陪多項式、チェビシェフの多項式といった直交多項式の背景に、ストゥルム・リウビル理論があります。
以上、直交多項式とは何か、ルジャンドル多項式を例に紹介してきました。
線形代数で考える内積や直交という概念は、数ベクトルに限らず、関数に対しても有効です。例えば、三角関数の直交性がフーリエ級数展開に役立つ話はよく知られています。
それ以外の例として、ルジャンドル多項式のような直交多項式・直交関数系があること、線形代数と微分方程式に結び付きがあることを、今回の話で感じてもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2014-09-14T00:00:01Z)
¥72,461
共立出版 (1982-07-09T00:00:01Z)
¥788 (中古品)
世界標準MIT教科書 ストラング:線形代数イントロダクション
近代科学社 (2015-12-22T00:00:01Z)
¥14,721 (コレクター商品)
東京大学出版会 (2019-03-08T00:00:00.000Z)
¥1,870
こちらもおすすめ
直交ベクトルの線形独立性、正規直交基底、直交行列について解説