線形代数における座標・成分・基底とは何か

どうも、木村（@kimu3_slime）です。

線形代数学では、線形写像やその表現行列、基底の変換といったテーマを扱います。

それらを学ぶためには、まず座標と基底の関係、座標とはそもそもなんだったのかを知っておく必要があるでしょう。今回はそれを紹介します。

2次元の座標
線形空間における座標
こちらもおすすめ

2次元の座標

簡単な例として、2次元のユークリッド空間\(\mathbb{R}^2\)について考えましょう。

その要素は、一般的に\(x= (x_1,x_2)\)と成分表示されます。平面に直交する軸を書いて、横方向を\(x_1\)軸、縦方向を\(x_2\)軸と呼び、座標平面と呼ばれる場所に図を書くこともよくありますね。（中学校や高校では、軸の名前を\(x,y\)とすることが多いでしょう。）このような座標のとり方を、デカルト座標（Cartesian coordinate）と呼びます。

さて、座標とは一体何なのでしょうか。平面上の点（ベクトル）を表すためには、何かしらの軸が必要です。線形代数の考え方では、それらの軸は基底に対応しています。

デカルト座標とは、標準基底\(e_1=(1,0)\)、\(e_2 =(0,1)\)により定まる座標のことと言えます。標準基底を使って、一般的なベクトル\(x\)を線形結合で表せば、\(x=x_1e_1+x_2 e_2\)と表せます。この関係式を省略したものが、\(x=(x_1,x_2)\)という成分表示と言えます。\(e_1\)が\(x_1\)軸、\(e_2\)が\(x_2\)軸に対応するベクトルです。

実は、平面において\(e_1=(1,0)\)、\(e_2 =(0,1)\)という基底を入れるのは、よくある考え方ですが、別の基底を入れて考えることもできます。

例えば、\(a_1 =(1,1)\)、\(a_2=(-1,1)\)というベクトルを考えましょう。\(a_1,a_2\)は\(\mathbb{R}^2\)において基底となっています。

実際、係数を\(c_1,c_2\)と置いて、\(x=(x_1,x_2)=c_1a_1+c_2a_2\)と新たなベクトルで表してみましょう。\(c_1,c_2\)について整理すれば、\(c_1=\frac{x_1 +x_2}{2}\)、\(c_2 =\frac{-x_1+x_2}{2}\)となります。\(a_1,a_2\)を軸にして見れば、\(x\)というベクトルは\((\frac{x_1 +x_2}{2},\frac{-x_1+x_2}{2})_{a_1,a_2}\)と成分表示されるわけです。

具体的には、\((2,1)=2e_1+e_2\)というベクトルを考えましょう。これを\(a_1,a_2\)で表せば、\(\frac{3}{2}a_1 -\frac{1}{2}a_2\)となります。

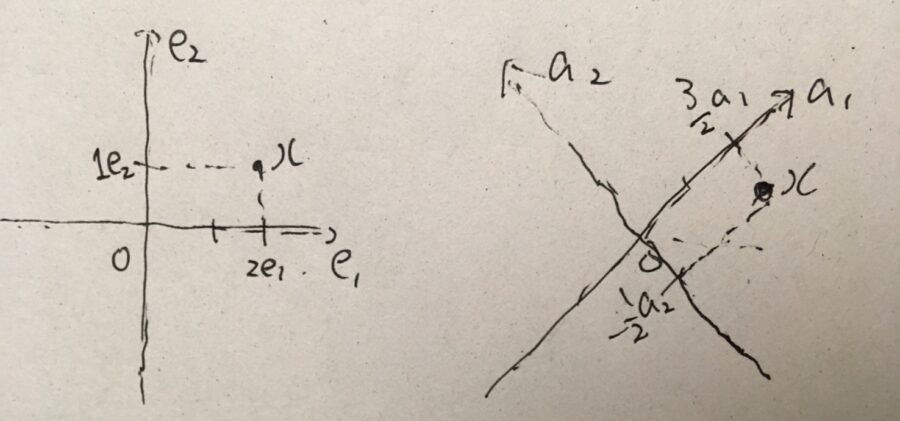
普通、単に\((2,1)\)と書いたら、それは\(2e_1+e_2\)のことを指すでしょう。そう解釈するということは、標準座標\(e_1,e_2\)を使っているということなのです。平面の点（ベクトル）を表すためには基底さえあれば良いので、別の見方をすることもできます。例えば、\(a_1,a_2\)を使えば\(\frac{3}{2}a_1-\frac{1}{2}a_2\)として見れるわけです。基底を変えれば、同じベクトルが別の成分表示に移り変わります。

\(e_1,e_2\)や\(a_1,a_2\)は直交する（互いに内積が0になる）基底です。直交基底による座標の表し方を、直交座標（orthogonal coordinates）と呼びます。

直交座標でない座標系を考えることができます。例えば、\(e_1,a_1\)という組み合わせも、基底なので座標系として使えます。これは軸と軸が直交していない座標系で、斜行座標（oblique coordinate）と呼ばれるものです。

例えば、\((2,1)= e_1+a_1\)です。この座標で見れば、\((1,1)_{e_1,a_1}\)という成分として見れるわけですね。

線形空間における座標

線形代数学では、ユークリッド空間\(\mathbb{R}^N\)以外の、一般的な線形空間\(V\)をも考えます。

例えば、行列のなす線形空間、数列のなす線形空間、関数のなす線形空間、多項式のなす線形空間やそれらの部分空間です。

数ベクトル以外の一般的な線形空間\(V\)というと、どうも抽象的に思えるかも知れません。

しかし、\(V\)に（有限個からなる）基底があれば、数ベクトルと同じように座標を入れて成分表示を考えられるのです。

例えば、2次の正方行列のなす線形空間において、\(E_1=\begin{pmatrix}1 &0 \\0 &0 \end{pmatrix},E_2=\begin{pmatrix}0 &1 \\0 &0 \end{pmatrix}\)、\(E_3 =\begin{pmatrix}0 &0 \\1 &0 \end{pmatrix},E_4 =\begin{pmatrix}0 &0 \\0 &1 \end{pmatrix}\)は基底です。この基底を使えば、例えば単位行列は\(I=E_1+0E_2+0E_3 +E_4\)と表せます。すなわち、\(I\)は\((1,0,0,1)_{E_1,E_2,E_3,E_4}\)と4つの成分によって表示ができているわけです。

フィボナッチ数列を定める漸化式を満たす数列のなす集合\(V:=\{\{a_n\} \mid a_{n+2} = a_{n+1}+a_n\}\)は、線形空間となります。そこでは、公比が\( \frac{1\pm \sqrt{5}}{2}\)である等比数列を基底として選ぶのが便利でした。\(a_1=1,a_2=1\)を満たす数列（フィボナッチ数列）は、\(a_ n = \frac{1}{\sqrt {5}}(\frac{1+ \sqrt{5}}{2} )^n -\frac{1}{\sqrt {5}} (\frac{1- \sqrt{5}}{2} )^n\)と表されます。基底を\(b,c\)とすれば、\(a= \frac{1}{\sqrt{5}}b-\frac{1}{\sqrt{5}} c\)という成分表示を持っているわけです。

詳しくは：漸化式（フィボナッチ数列）を線形代数（線形空間、固有ベクトル）で解く方法を解説

関数のなす空間では、いろいろな基底を考えることがあります。

例えば、\(1,x,x^2,\dots,x^n\)によって張られる部分空間において、

\[ \begin{aligned}f(x) = \sum_{k=0}^n\frac{f^{(k)} (0)}{n!}x^k\end{aligned} \]

と展開すれば、これはテイラー展開です。テイラー展開の主張は、多項式\(1,x,x^2,\dots,x^n\)による基底で関数を表示すると、\((f(0),f^{\prime}(0),\dots,\frac{f^{(k)} (0)}{n!})\)という成分表示を持つと言えます。

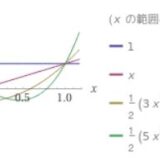
基底の入れ方を変えれば、係数、関数の座標は変わってきます。関数空間において、三角関数\(\{\cos 0x, \sin kx\}_{k=1}^5\)によって生成される部分空間を考えるとしましょう。そこで\(f\)が

\[ \begin{aligned}f(x)= \frac{1}{2} + \frac{2}{\pi} \sin x + \frac{2}{3\pi} \sin 3x + \frac{2}{5\pi} \sin 5x\end{aligned} \]

と表されるとき、その座標は\((\frac{1}{2},\frac{2}{\pi},0,\frac{2}{3\pi} ,0,\frac{2}{5\pi} )\)です。このようなフーリエ級数展開も、三角関数という基底を使って関数を成分表示していると言えます。

参考：線形代数の応用：関数の「空間・基底・内積」を使ったフーリエ級数展開

以上、線形代数における座標、成分、基底とは何か紹介してきました。

座標や成分というのは当たり前に存在しているように思えますが、実は基底の選び方に依存したものです。中学校や高校の数学では、ユークリッド空間において標準基底を考えることが多いでしょうが、そうでない基底の選び方、座標や成分表示の方法があります。

逆に、基底さえあれば、よくわからない線形空間においても、座標や成分というものが考えられるわけです。今回の話が、座標や基底を考えることへの視点を広げるものとなれば嬉しいです。