ベッセルの不等式・パーセバルの等式とは：有限のケースで証明

どうも、木村（@kimu3_slime）です。

フーリエ解析や関数解析では、ベッセルの不等式やパーセバルの等式と呼ばれるものが登場します。今回は、それを線形代数の枠組み、有限のケースについて紹介し、証明します。

ベッセルの不等式
パーセバルの等式
こちらもおすすめ

ベッセルの不等式

ベッセルの不等式は、次のような不等式です。

\(V\)を（有限次元の）内積空間、\(a_1,\dots,a_n\)を正規直交なベクトルの集まりとする（必ずしも基底でなくて良い）。任意の\(x \in V\)に対して、

\[ \begin{aligned}\sum _{k=1} ^n |\langle x, a_k\rangle|^2 \leq \|x\|^2\end{aligned} \]

が成り立つ。

ユークリッド空間\(V= \mathbb{R}^N\)において、\((e_k )_{k=1}^n ,n<N\)という標準基底（第\(i\)成分が1、他は0）を考えましょう。\(x=(x_1,\dots,x_n)\)と成分表示したとき、ユークリッド内積を計算すれば、\(\langle x,e_k\rangle =x_k\)です。したがって、ベッセルの不等式は

\[ \begin{aligned}\sum _{k=1} ^n x_k^2 \leq \|x\|^2\end{aligned} \]

と表されます。左辺は右辺の部分的な和なので、当然これは成り立ちますね。

有限フーリエ級数のなす関数空間\(V_n:= \{f:[-\pi,\pi] \to \mathbb{R} \mid f(x)=a_0+\\ \sum_{k=1} ^n (a_k \cos kx +b_k \sin kx) ,\quad a_k,b_k \in \mathbb{R}\}\)において、正規直交なベクトル\(\{ \frac{1}{\sqrt{2\pi}}\cos 0x, \frac{1}{\sqrt{\pi}}\cos kx, \frac{1}{\sqrt{\pi}}\sin kx\}_{k=1}^{n}\)を考えましょう。内積は、直交性を使って計算すると

\[ \begin{aligned} \langle f, \frac{1}{\sqrt{2\pi}}\cos 0x\rangle &=\langle a_0 \cos 0x, \frac{1}{\sqrt{2\pi}}\cos 0x\rangle \\ &= \sqrt{2\pi}a_0 \end{aligned} \]

\[ \begin{aligned} \langle f, \frac{1}{\sqrt{\pi}}\cos kx\rangle &=\langle a_k \cos kx, \frac{1}{\sqrt{\pi}}\cos kx\rangle \\ &= \sqrt{\pi}a_k \end{aligned} \]

\[ \begin{aligned} \langle f, \frac{1}{\sqrt{\pi}}\sin kx\rangle &=\langle b_k \sin kx, \frac{1}{\sqrt{\pi}}\sin kx\rangle \\ &= \sqrt{\pi}b_k \end{aligned} \]

となるので、ベッセルの不等式は

\[ \begin{aligned}\pi(2a_0^2 +\sum_{k=1}^n a_k ^2 +b_k^2) \leq \int _{-\pi}^\pi f(x)^2dx\end{aligned} \]

となりました。右辺は一見して、\(n\)に依存していない形になっているのがポイントです。もし右辺が有限値ならば（二乗可積分ならば\(f \in L^2\)）、左辺は\(n\)が何であっても有限値であると議論できそうですね。

（実は、\(n\to \infty\)でもベッセルの不等式は成り立つことが知られています。そこから、フーリエ係数\(a_k,b_k\)は\(k\to \infty\)で0に近づくこと：リーマン・ルベーグの補題が導けます。）

では、ベッセルの不等式を証明しましょう。

その理屈は、コーシー・シュワルツの不等式の証明と非常によく似ています。それは、一方のベクトルをもう一方のベクトルへ正射影したときの誤差が0以上という理屈でした。

ベッセルの不等式は、一般のベクトル\(x\)を\(a_1,\dots,a_k\)の張る線形空間へと直交射影したときの誤差が0以上という主張と同じです。

まず、\(x=\sum _{k=1} ^n \langle x,a_k\rangle a_k +(x-\sum _{k=1} ^n \langle x,a_k\rangle)a_k \)と分解できるので、\(e:=x-\sum _{k=1} ^n \langle x,a_k\rangle a_k\)と置きましょう。\(e\)は\(a_1,\dots,a_k\)すべてと直交しています。

ノルムの性質より、\(\|e\| \geq 0\)です。一方、直交性を利用して内積を展開計算してみると

\[ \begin{aligned} \|e\|^2&= \langle x-\sum _{k=1} ^n \langle x,a_k\rangle a_k,x-\sum _{k=1} ^n \langle x,a_k\rangle a_k \rangle \\&= \langle x,x\rangle -2 \sum _{k=1}^n|\langle x,a_k\rangle |^2+\sum _{k=1}^n |\langle x,a_k\rangle |^2\langle a_k,a_k\rangle \\ &= \|x\| – \sum _{k=1}^n|\langle x,a_k\rangle |^2\end{aligned} \]

となります。これが0以上なので、ベッセルの不等式\(\sum _{k=1} ^n |\langle x, a_k\rangle|^2 \leq \|x\|^2\)が得られました。

パーセバルの等式

パーセバルの等式（Parseval’s identity）は、直交するベクトルが正規直交基底のときは、ベッセルの不等式において等式が成り立つという主張です。

\(V\)を（有限次元の）内積空間、\(a_1,\dots,a_n\)を正規直交基底とする。任意の\(x \in V\)に対して、

\[ \begin{aligned}\sum _{k=1} ^n |\langle x, a_k\rangle|^2 = \|x\|^2\end{aligned} \]

が成り立つ。

ユークリッド空間\(V= \mathbb{R}^N\)において、\((e_k )_{k=1}^N \)という標準基底を考えましょう。\(\langle x,e_k\rangle =x_k\)なので、パーセバルの等式は

\[ \begin{aligned}\sum _{k=1} ^N x_k^2 = \|x\|^2\end{aligned} \]

となります。標準的な内積・ノルム（ユークリッド内積・ノルム）を考えれば、明らかな等式ですね。左辺は\(e_k\)方向の大きさを全成分足し合わせたもの、右辺は\(x\)のノルムを計算したものです。標準基底以外の正規直交基底を考えると、非自明になるでしょう。

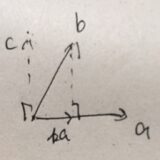
これの特殊なケースには、ピタゴラスの定理（三平方の定理）が含まれています。平面\( \mathbb{R}^2\)において、斜辺を\(x=(x_1,x_2)\)と表すとき、他の辺は\((x_1,0),(0,x_2)\)と表せます（これらは直交し、直角三角形ができている）。\(a=\|(x_1,0)\|,b=\|(0,x_2)\|\)、\(c=\|x\|\)と置けば、\(a^2+b^2 =c^2\)が成り立つというのがピタゴラスの定理です。これはパーセバルの等式の形をしています。

有限フーリエ級数のなす関数空間\(V_n\)において、パーセバルの等式は

\[ \begin{aligned}\pi(2a_0^2 +\sum_{k=1}^n a_k ^2 +b_k^2) = \int _{-\pi}^\pi f(x)^2dx\end{aligned} \]

となります。

（パーセバルの等式は、完全正規直交基底という条件で、\(n\to \infty\)で成り立ちます。フーリエ級数でなく、フーリエ変換についても同様の等式が成り立ち、それはプランシュレルの定理と呼ばれています。）

（バーゼル問題と呼ばれる級数 \(\sum_{k=1}^\infty \frac{1}{k^2} = \frac{\pi^2}{6}\)も、パーセバルの等式から導けます。）

では、パーセバルの等式を証明しましょう。

\(x \in V\)とし、正規直交基底で展開すると\(x= \sum_{k=1}^n x_k a_k\)と表せます。両辺で\(a_k\)との内積を取れば、直交性から\(x_k =\langle x,a_k\rangle\)です。これを使って、内積を展開してみましょう。

\[ \begin{aligned} \|x\|^2&= \langle\sum_{k=1}^n x_k a_k,\sum_{k=1}^n x_k a_k \rangle \\ &= \sum_{k=1}^n x_k \langle a_k,\sum_{k=1}^n x_k a_k \rangle \\&=\sum_{k=1}^n x_k \langle a_k, x_k a_k \rangle \\&=\sum_{k=1}^n |x_k|^2 \langle a_k, a_k \rangle \\&= \sum_{k=1}^n|\langle x,a_k\rangle|^2\ \end{aligned} \]

と等式が成り立つことが言えました。

以上、ベッセルの不等式、パーセバルの等式とは何か、有限のケースで証明してきました。

これらの不等式、等式は、完備な内積空間（ヒルベルト空間）、完全正規直交基底のケースに一般化されます。

フーリエ級数展開の議論で初めて目にするとひるむかもしれませんが、今回のように有限次元のケースで考えれば、成り立つのがもっともと思える主張でしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。