どうも、木村(@kimu3_slime)です。
今回は、数学はなぜ重要か:数学と科学の関係を考えるということで、SFAA(Science for All Americans)を読んで考えたことを書こうと思います。
「数学は難しい」の裏にあるもの
「数学は難しいものだ」という印象を人から聞くたびに、「数学そのものは簡単な部分を取り出せば簡単なのに、教育によってそれを感じる機会がないのだな」と、(過剰な言い方だが)数学教育の敗北を感じる。
数百年前は微積は最先端だったが、今や高校で学べる程度に道筋は整えられたわけで。— 木村すらいむ (@kimu3_slime) October 12, 2022
僕が「数学をやっている」という話を他人にするとき、しばしば「数学は難しくてよくわからない」という反応が返ってきます。
確かに、例えば高校数学は万人にとって簡単とはいい難いでしょう。高校の数学が「できる」人でも、大学数学の講義を聞いてから、「数学は一旦捨てた、後になって勉強しておけばよかった」と思う人もいます。
実際僕も、大学数学をより簡単に学べるように、講義や教科書に書かれていない話を補いながら文章を書いています。
しかし、「難しい」という言葉の背景として、本当に「難しい」が課題なのでしょうか? 簡単になれば学ぶのでしょうか? そういう人もいるでしょうが、それだけではないとも思います。
すなわち、数学的を簡単に学ぶ方法が用意されなかっただけではなく、自分の人生における数学を学ぶ意義、数学と科学や社会の関連性をあまり知る機会がないという問題点があるのではないでしょうか?
「数学は何の役に立つの?」と聞かれるとき、僕はしばしば次の画像のような説明をします。

数学は科学の言語として他の科学の役に立って、それを利用して工学・技術が発展し、結果として社会や日常生活がより豊かなものになっていくと。
数学の意義を感じてもらうには、まず科学(的活動)の意義を知ってもらうのがわかりやすいかと思います。僕が受けてきた学校教育では、科学や数学の「中身」を叩き込む授業はあっても、科学や数学の意義を知る機会はあまりなかったので。
そこで科学リテラシーの重要性を提言する本「SFAA(Science for All Americans)」を読み、特に数学と科学の関係や意義を言語化したいと思います。
数学と科学の関係性、意義
人間の活動としての科学、数学
「科学・数学は非人間的だ」「科学・数学は間違えない」「科学・数学は完成していて、今では何も調べることは残っていないのでは」という一般の人からの指摘はしばしばあります。
確かに、学校で学ぶ「完成された」教科書や、手順のみを学ぶ授業から、そのような印象を受けとることがあるのもわかります。
数学、それ以前に科学に対する印象として、次のことは重要なので伝えることが多いです。
- 科学は人間の活動である
- 僕たちが生きるこの世界がどうなっているかを知ろうとし、知ることができると考えている。「神のみぞ知る」で終わらせない、チャレンジング。
- 科学は分業。たくさんの問題を「天才」が一気に解決してくれるわけではない。問題を分野に分けて、みんなで少しずつ解いていく。部分的な回答を生み出し、共有する。それを人類は数百年やってきた。
- 蒸気船、鉄道、工場、医療、電気、コンピュータなどの技術は社会を豊かにしてきた。そうした技術の背後には物理学、化学、生物学、計算機科学などの科学がある。そしてその基礎に数学がある。
- 一方で副作用、例えば核兵器の利用や生体実験、環境問題もある。研究倫理の重要性は増してきていて、また社会問題を改善する手段としても科学は必要になる。
- 科学は「正解」を追求しようとする試みであるが、100%絶対的な「正解」は基本的にない。
- だからこそ、理論は研究者によって相互に検証され、変化している。例えば相対性理論の発見。
- 古くから知られ永久に正しいと言われるような科学の結果はあるが、それは検証を耐えてきた結果である。
- 世界を理解するために、理論はしばしば単純化をする。実験は同じ状況を制御し整える。だから、理論・実験的に正しいことと、現実に適用することのギャップは少なからずある。社会で科学を応用・利用する人も、科学を理解する必要がある。
- 何にでも答えられるわけではない。わかっていないことはたくさんある。
- 逆説的に、「科学的に言って絶対にこうだ」という手の主張を疑うべき(笑)。できるだけ権威によらず判断する。
言語としての数学
数学と科学の関係性を説明するのに、最もわかりやすいと思ったのは、言語としての数学です。
数学は科学の主要言語である。数学の記号的言語は、科学的な考えを明確に表現するのに非常に有用であることが分かってきた。a=F/mという表現は、物体の加速度が物体に加えられた力とその質量に依存することを示す単なる省略形ではなく、それらの変数の間の量的関係を正確に表現しているのである。さらに重要なことは、数学は科学の文法、つまり科学的な考えやデータを厳密に分析するためのルールを提供することである。
引用:SFAA(翻訳はDeepL)
説明を補いましょう。\(a= \frac{F}{m}\)は物理学、特に力学における基本的な法則:ニュートンの運動方程式を表しています。
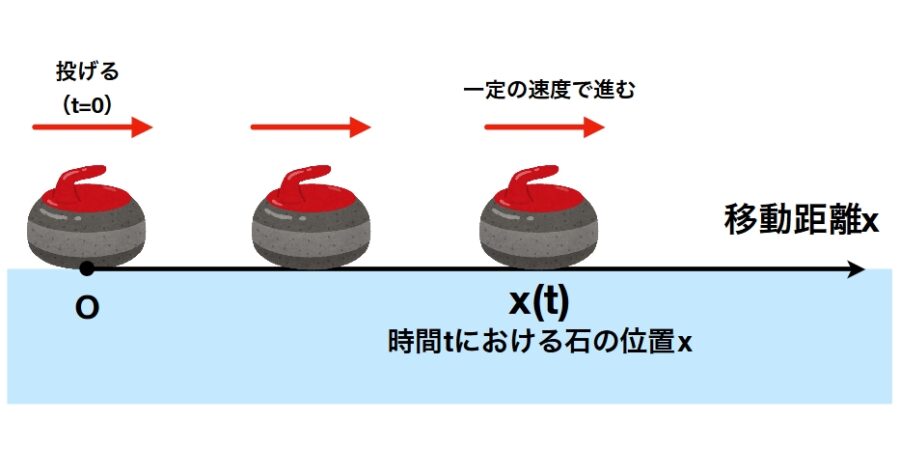
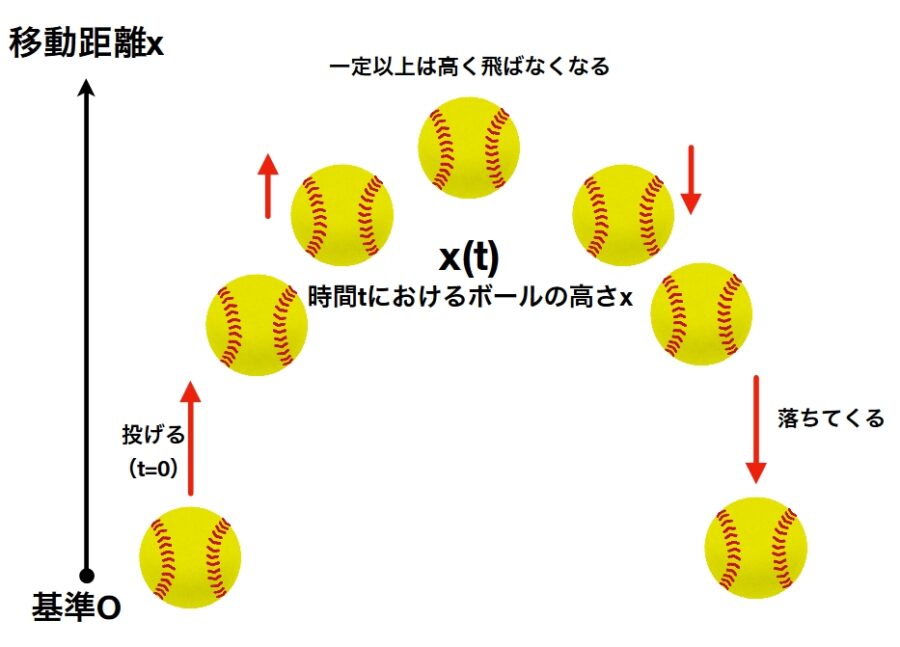
この方程式を使えば、カーリングで石が滑り続ける現象(等速直線運動)や空に投げたボールが落ちてくる現象(放物運動)が説明できます。
バネの振動運動(単振動)も、\(a= \frac{F}{m}\)によって説明できます。
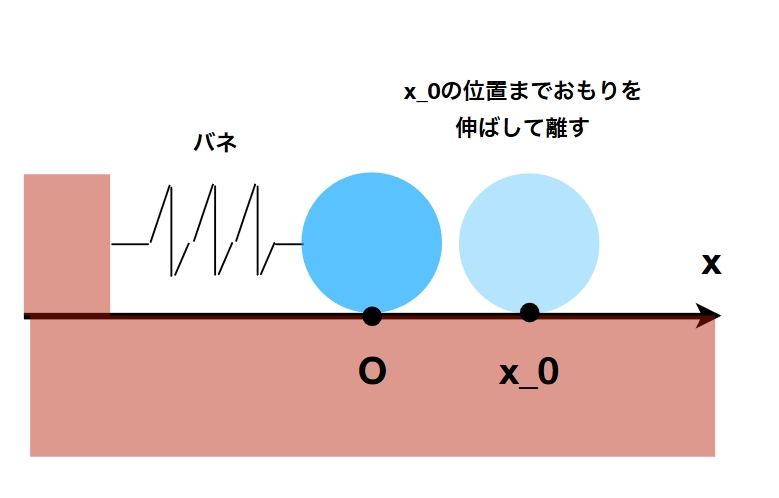
参考:おもりバネの運動:単振動の運動方程式、微分方程式の解き方
このように、物理現象を説明するときに、数式は至る所で使われています(物理に限りませんが、物理は特にその傾向が強いです)。
数学はさまざまな基本法則を表現する「言語」と言えますが、どうして言語と形容するのでしょうか。
それは抽象化をしているからです。
ニュートンの運動方程式では、質量を\(m\)、力を\(F\)、加速度を\(a\)と文字で表しました。「加速度は力を質量で割ったものに等しい」も本質的に同じ表現ですが、やはり記号を使ったほうが、関係性がわかりやすく計算しやすいです。
そもそも、数字は抽象化をしています。小学校で扱うような問題、「いくつありますか」の文章題や「つるかめ算」は、何の「もの」だろうが、つるとかめでなかろうが使えるものです。個別の特徴をある程度忘れ去って、数量や文字として扱うことで、単純に説明できる事柄は少なくないです。
抽象化の応用の例としてわかりやすいのは、関数の考え方です。
「もし地球の平均気温が10年で0.2度上昇し続けるならば、50年後には何度上昇するでしょうか?」という問題は、中学校で関数の考え方を学べば解けます。
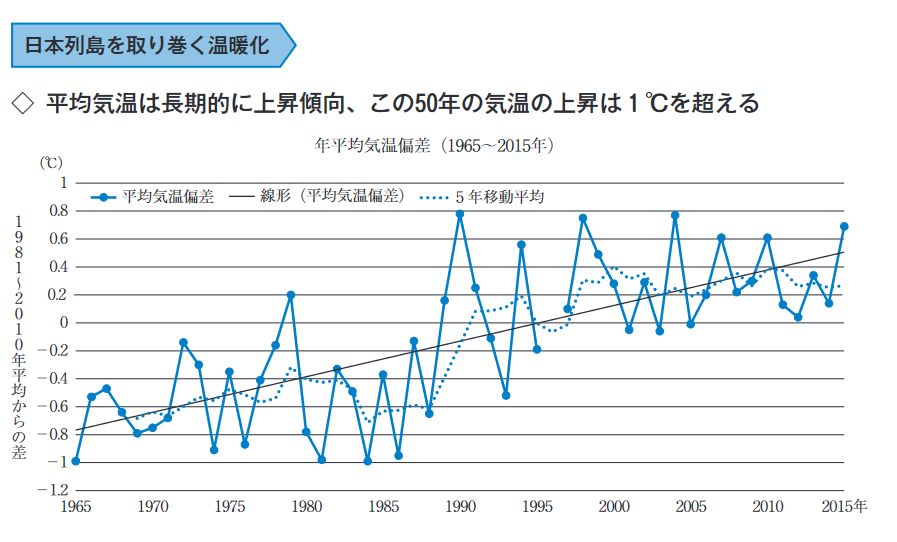
科学の特徴には「説明と予測」がありますが、まさしくそれは数学でいう関数の考え方の応用です。2つの量の変化の関係を分析するのは、科学の基本と言えます。
関数の考え方をより発展させたものが、数理モデルです。
たとえばニュートンの運動方程式は数理モデルの一種です。「天体の動きもリンゴの落下も同じの法則に従っているのではないか」という考え方です。
どんな関数(現象)なのかを分析するだけでなく、どうしてこんな関数(現象)が表れるのかを統一的に説明する手段が数理モデルと言えます。

参考:なぜ中学・高校数学を学ぶのか 数理モデルとしての微分方程式
数理モデルの考え方は例えば生物学にも利用されています。生き物の斑点や縞模様は、チューリングパターンとして、同一の方程式(反応拡散方程式)によって説明できることが知られています。

画像引用:生き物のからだの模様をつくりだす仕組みにズーム・イン! – 生命科学DOKIDOKI研究室
参考:生き物の模様は数式で決まる? チューリング・パターンとは
数学の文字や関数といった考え方は、抽象化をしているので、相手を選ばずに実にさまざまな分野で利用できる、というわけですね。
紹介し始めるとキリがありませんが、どんな科学の分野でも、学べば多かれ少なかれ数学の必要性を感じられるでしょう。
以上、数学はなぜ重要か:数学と科学の関係について考えてきました。
「数学ができる・できない」という基準で考える人は少なくないです。そこで「簡単に学ぶ方法」を伝えるだだけでなく、「科学は面白いし社会にとって重要」「数学はその言語の役割を果たす」という話もできると良いのだな、と再認識しました。
木村すらいむ(@kimu3_slime)でした。ではでは。