どうも、木村(@kimu3_slime)です。
高校数学で学ぶベクトルは、何の役に立つのでしょうか。ベクトルが日常生活で利用される実用例、活用例を紹介します。
ビジネス用語
ビジネス用語としての「ベクトル」は、「人の考え方や価値観を向きに例えたもの」として使われます。
「ベクトルが合う・合わない」「ベクトルが違う」、など。
(1から転じて)方向性をもつ力。物事の向かう方向と勢い。「各省庁間のベクトルの大小を比較する」「彼とはベクトルが合う」「組織内の各人がばらばらにベクトルを立てる」
引用:ベクトル – goo辞書
これは数学における本来の意味でのベクトルというよりは、流用だと思いますが、一応紹介しておきました。
物理におけるベクトル
物理学では、ベクトルの考え方を駆使します。
物の動きを予測する分野、力学では、斜めに飛ばされた物体の運動が考えられます。
例えば、野球で弾を投げたり、サッカーでボールを蹴るとき、物体は斜めに飛びます。地面に水平な方向\(x\)と鉛直な方向\(y\)を考えると、物体の速度ベクトルは\(v=(v_x ,v_y)\)と、2つの成分に分解して考えることができます。これがベクトルの考え方です。
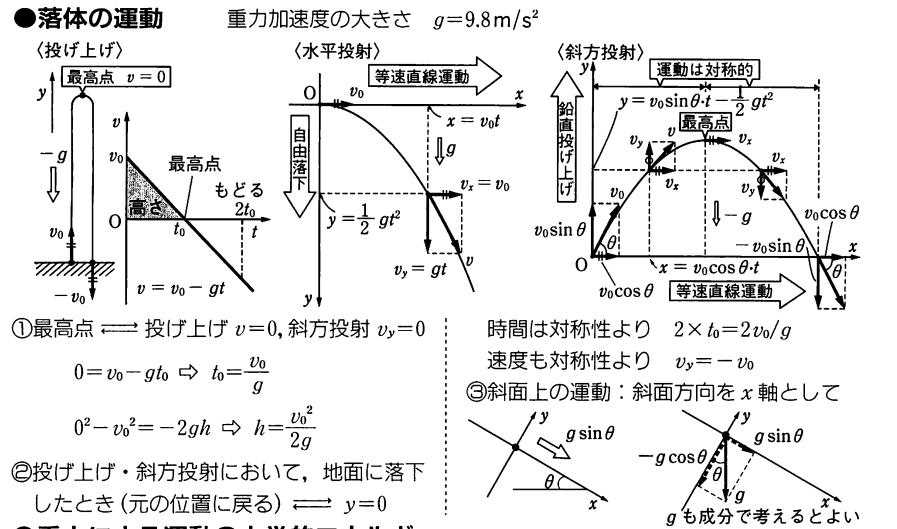
斜めの速度ベクトル\(v\)は複合的なものと考え、x方向\(v_x\)とy方向\(v_y\)に分解して考える。水平方向には何も力が働かずに、等速直線運動を続けます。鉛直方向には重力が働くので、だんだんと落下していきます。これがいわゆる放物運動です。
ななめに飛ばすときの初速度を\(v_0\)、\(x\)軸の角度を\(\theta\)とするとき、x方向の速度は\(v_x = v_0 \cos \theta\)、y方向の速度は\(v_y =v_0 \sin \theta\)と三角関数で表せます。これはベクトルだけでなく、三角関数の応用にもなっていますね。
直線運動のような単純な現象を考えるならば、ベクトルの考え方は必要ありません。しかし、私達の生きる世界は、基本的には3次元の空間と考えられます。その世界での現象を考えるには、ただひとつの数ではなく、数の組み合わせ=ベクトルが必要となるわけです。
さまざまな物理量は、一般的にはベクトルの枠組みで捉えられます。速度、加速度、力、電場(電界)、磁場(磁界)などはベクトルを使って分析されてきました。
物理現象の多くは、微積分を使って定式化されますが、ベクトルと微積分を組み合わせた分野は、ベクトル解析として知られています。
平面や空間上の各点に対し、ベクトルを対応させるとき、その関係はベクトル場と呼ばれます。これは風や水の流れの可視化によく使われるものです。
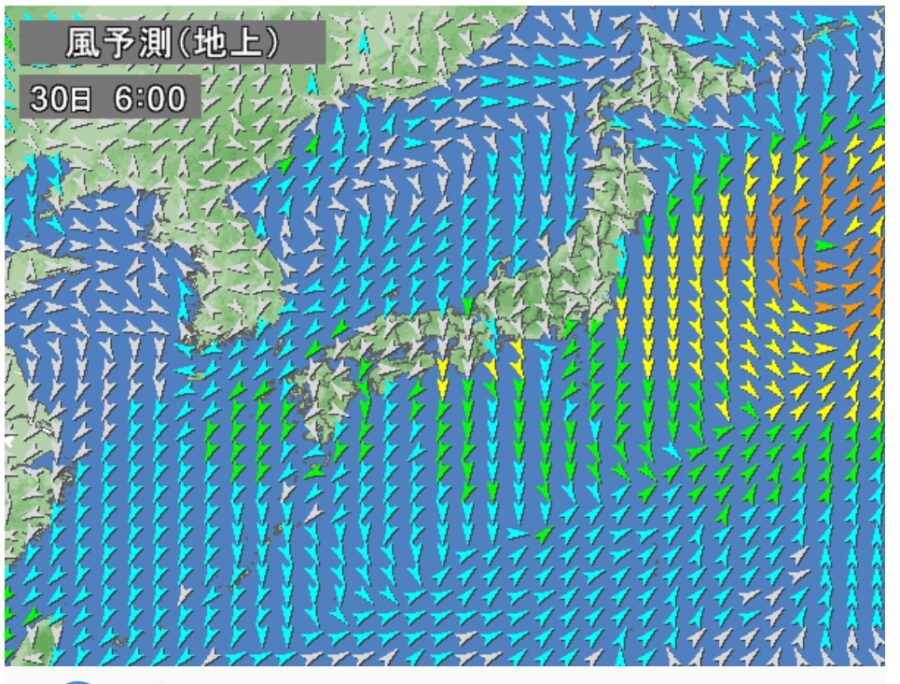
画像引用:全国の風予測 – Yahoo!
参考:ベクトル値関数をベクトル場として描いてみよう:ヤコビ行列と線形近似
熱の伝導や化学物質の拡散、波の移動などの現象は、時間\(t\)と空間\(x\)の変数を組み合わせて調べる必要があり、そこでベクトルの考え方は欠かせません。
空間と時間変化を伴う現象を調べる枠組みとして、熱伝導方程式や波動方程式などの偏微分方程式がありますが、ベクトルの考え方はその基礎となっています。
参考:なぜ偏微分を学ぶ? フーリエの熱伝導方程式を例に、波の重ね合わせの原理はなぜ成り立つ? 波動方程式入門
データ:数の組としてのベクトル
アサガオのつるの長さを計測して、次のようなデータが得られたとしましょう。
| 実際のデータ | |
| 日数 | 長さ |
| 3 | 5 |
| 6 | 11 |
| 9 | 16 |
| 12 | 20 |
このような多次元のデータは、数学的にはベクトルとして捉えられます。つまり、長さのベクトルを\(x=(5,11,16,20)\)といったようにいくつかの数の組として表現できるわけです。
高校の数学でのベクトルでは、矢印としてのベクトル(幾何ベクトル)を導入し、2次元や3次元のベクトルのみを考えます。
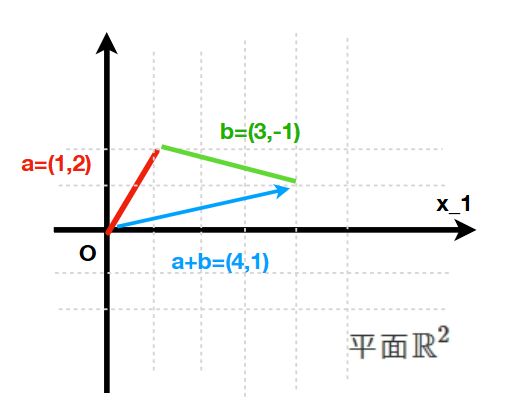
しかし、ベクトルとは数の組(数ベクトル)シンプルに扱える枠組みなのです。さきほどのデータ\(x=(5,11,16,20)\)は、4次元(\(\mathbb{R}^3\))のベクトルです。たくさんの数値を同時に捉えるならば、10次元、100次元、一般には\(n\)次元のベクトルが必要となります。
プログラミングでは多次元のデータをひとまとめにするために、配列という考え方があります。これは数学的にはベクトルです。
エクセルなどの表計算ソフトでは、マス目に数値を入れて、それらの合計や平均を計算することができます。その考え方もまさしくベクトル(や行列)です。
統計学では、たくさんの数をひとつのデータ(ベクトル)として扱います。昨今ではビッグデータの解析などが話題となっていますが、その理論的な基礎としてベクトルの知識は欠かせません。
参考:Pythonで統計量関数(平均、中央値、分散、相関係数)を作り、可視化しよう
僕たちは生活の中で、気づかずに数を利用しています。お金の貸し借りならば正負の数(整数)を、長さや面積では実数を使っているわけです。ベクトルとは多次元的な数であり、そうと意識することがなかったとしても、いくつかの数を同時に扱うときに当たり前に使われています。
大学数学を学んでいると、数ベクトルを使わないことはあまりないと言っていいくらい、どこにでも登場します。整数や実数をわざわざ「何に使うのか」と考えないくらいに、ベクトルは数の多次元的な表現として基本的なものです。

ベクトル・行列の発展:線形代数学
ベクトルや行列を理論的に扱う分野は、大学では線形代数学として学ばれています。
画像データは数値の列(ベクトルや行列)として表現できますが、その拡大縮小、回転などはベクトルの変換(行列)によって表現できます。
検索エンジンGoogleにおけるランキングシステムでも、スコアの算出方法として線形代数が利用されています。離散的な構造を扱う離散数学・グラフ理論においては、ベクトルの考え方は基本的です。
線形代数学の応用:CG・画像処理(拡大縮小・反転、回転、せん断)について
なぜ線形代数を学ぶ? Googleのページランクに使われている固有値・固有ベクトルの考え方
Julia(Graphs)でグラフ理論におけるグラフ作成、次数、隣接行列を求める方法
行列を使うと、多次元的ながら最もシンプルな問題の枠組み、線形問題を定式化できます。
確率的に人々が移動するとどうなるか、無駄なく飲み物を生産するにはどうすれば良いか、家が売れているとき林業への売上の影響はどうなるか、これらはすべて線形代数の考え方で分析できます。
行列を使うと、中学校で学んだような連立1次方程式(線形方程式)を、変数が2つでなく、100、1000といったたくさんの変数を含む問題が解けるようになります。
コンピュータによる数値計算、シミュレーションでは、数学的な問題を線形代数の問題に落とし込みます。コンピュータでは理論的な数(無限に細かい区間)を扱えないので、有限個に細かく分けて(高次元のベクトルを考えて)処理する必要があるわけです。
参考:1次方程式を行列で解くメリット・方法・条件について、幾何学的に見る
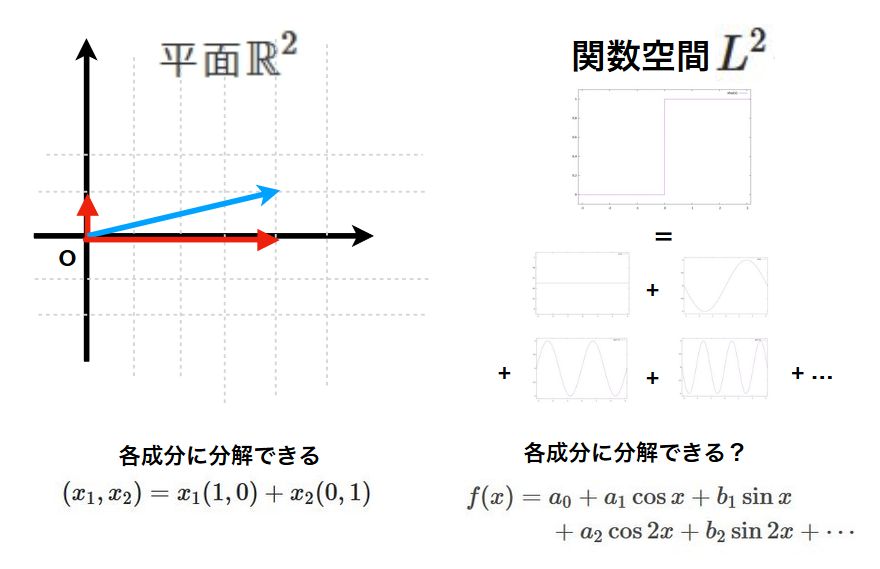
線形代数では、数ベクトルだけでなく、ベクトルのように扱えるもの=抽象ベクトルを扱います。例えば、数列や関数もベクトルとして扱えるようになるわけです。
複雑な関数を、さまざまな周波数の三角関数の分解として捉えることができ、それはフーリエ解析と呼ばれています。複雑な関数を単純な関数に分解するという考え方は、まさにベクトル的ですね。
漸化式(フィボナッチ数列)を線形代数(線形空間、固有ベクトル)で解く方法を解説
線形代数の応用:関数の「空間・基底・内積」を使ったフーリエ級数展開
以上、ベクトルが日常生活で利用される実用例、活用例を紹介してきました。
斜めの運動や風の流れ、表計算ソフトや統計処理、CGやシミュレーションなどでベクトルは利用されています。
多次元的にものを考える、大量のデータをひとまとめにするときに、ベクトルの考え方が利用されていることに気づけば、数を使わない生活がないように、ベクトルを使わない生活がないことに気づくのではないでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
数研出版 (2021-11-06T00:00:01Z)
¥590 (中古品)
こちらもおすすめ
ベクトル値関数をベクトル場として描いてみよう:ヤコビ行列と線形近似
Pythonで統計量関数(平均、中央値、分散、相関係数)を作り、可視化しよう
線形代数学の応用:CG・画像処理(拡大縮小・反転、回転、せん断)について
なぜ線形代数を学ぶ? Googleのページランクに使われている固有値・固有ベクトルの考え方
Julia(Graphs)でグラフ理論におけるグラフ作成、次数、隣接行列を求める方法
1次方程式を行列で解くメリット・方法・条件について、幾何学的に見る
漸化式(フィボナッチ数列)を線形代数(線形空間、固有ベクトル)で解く方法を解説
線形代数の応用:関数の「空間・基底・内積」を使ったフーリエ級数展開